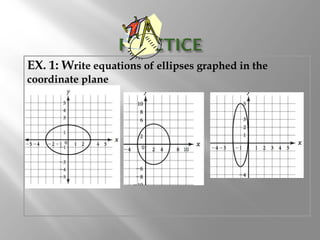
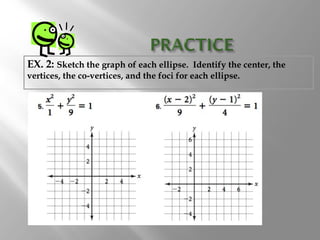
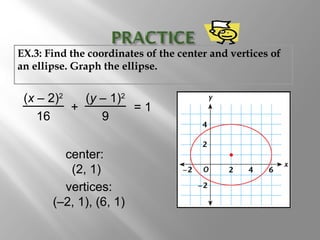
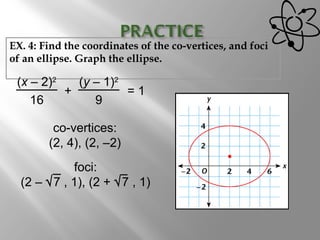
An ellipse is a curve where the sum of the distances from two fixed points (foci) is a constant. It is defined by the equation (x-h)2/a2 + (y-k)2/b2 = 1, where a and b are the lengths of the semi-major and semi-minor axes. The eccentricity e = c/a measures how oval the ellipse is, with a circle being e = 0 and e approaching 1 being very oval. Examples show how to graph ellipses from equations in standard form and identify features like foci, vertices, and co-vertices.

1. Definition of Ellipse
An ellipse is a locus of
all points (x,y) such
that the sum of the
distances from P to two
fixed points, F1 and F2,
called the foci, is a
constant.
P
F1 F2
F1P + F2P = 2a

2. Major axisCenter (h,k)
Minor axis VertexVertex
Co-vertex
Co-vertex
focus
Center (h,k)
Major Axes:
Minor Axes:
Vertices:
Co-vertices:
Foci:There are TWO cases of an ellipse:
Horizontal major axes and Vertical major axes

3. Horizontal Major Axis and C(0,0):
a2
> b2
a2
– b2
= c2
F1(–c, 0) F2 (c, 0)
y
x
V1(–a, 0) V2 (a, 0)(0, b)
(0, –b)
O
major axis = 2a
minor axis = 2b
x2
a2
y2
b2
+ = 1

4. a2
> b2
a2
– b2
= c2
(x – h)2
a2
(y – k)2
b2
+ = 1
Horizontal Major Axis and C(h,k):

5. F1(0, –c)
F2 (0, c)
y
x
V1(0, –a)
V2 (0, a)
(b, 0)(–b, 0)
O
Vertical Major Axis and C(0,0):
a2
> b2
a2
– b2
= c2
x2
b2
y2
a2
+ = 1
major axis = 2a
minor axis = 2b

6. a2
> b2
a2
– b2
= c2
Vertical Major Axis and C(h,k):
(x – h)2
b2
(y – k)2
a2
+ = 1

7. The early Greek astronomers thought that the planets
moved in circular orbits about an
unmoving earth. In the 17th century, Johannes Kepler
discovered that each planet travels around the sun in an
elliptical orbit

8. One of the reasons it was difficult to detect that orbits are elliptical is that
the foci of the planetary orbits are relatively close to the center, making
the ellipse nearly circular.
To measure the ovalness of an ellipse, we use the concept of eccentricity.
DEFINITION:
The eccentricity e of an ellipse is given by the ratio e = c/a
e e
1

9. EX. 1: Write equations of ellipses graphed in the
coordinate plane

10. EX. 2: Sketch the graph of each ellipse. Identify the center, the
vertices, the co-vertices, and the foci for each ellipse.

11. EX.3: Find the coordinates of the center and vertices of
an ellipse. Graph the ellipse.
center:
(2, 1)
vertices:
(–2, 1), (6, 1)
(x – 2)2
16
(y – 1)2
9
+ = 1

12. EX. 4: Find the coordinates of the co-vertices, and foci
of an ellipse. Graph the ellipse.
co-vertices:
(2, 4), (2, –2)
foci:
(2 – √7 , 1), (2 + √7 , 1)
(x – 2)2
16
(y – 1)2
9
+ = 1

13. EX.5: Graph the ellipse.
9x2
+ 16y2
– 36x – 32y – 92 = 0
standard form:
(x – 2)2
16
(y – 1)2
9
+ = 1

14. All rights belong to their respective
owners.
Copyright Disclaimer Under
Section 107 of the Copyright Act
1976, allowance is made for "fair
use" for purposes such as criticism,
comment, news reporting,
TEACHING, scholarship, and
research.
Fair use is a use permitted by
copyright statute that might
otherwise be infringing.
Non-profit, EDUCATIONAL or
personal use tips the balance in
favor of fair use.