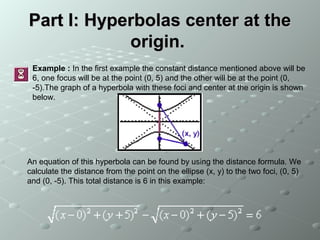
This document defines a hyperbola as the set of all points where the difference between the distances to two fixed points, called foci, is a constant. A hyperbola can be formed by slicing a cone with a plane parallel to the cone's vertical axis. An example hyperbola is shown with foci at (0,5) and (0, -5) and the points on the hyperbola satisfying the equation (x-0)^2/(4)^2 - (y-5)^2/(3)^2 = 1. Key features identified are the transverse axis connecting the foci, the distance a from the center to the foci, and the asymptotes that the branches approach but never reach

1. HYPERBOLAHYPERBOLA

3. DefinitionDefinition::
AA hyperbolahyperbola is all points found by keeping the difference of theis all points found by keeping the difference of the
distances from two points (each of which is called adistances from two points (each of which is called a focusfocus of theof the
hyperbola) constant. The midpoint of the segment (thehyperbola) constant. The midpoint of the segment (the transversetransverse
axisaxis) connecting the foci is the) connecting the foci is the centercenter of the hyperbola. Amof the hyperbola. Am
hyperbola can be formed by slicing a right circular cone with a planehyperbola can be formed by slicing a right circular cone with a plane
traveling parallel to the vertical axis of the cone. This effect can betraveling parallel to the vertical axis of the cone. This effect can be
seen in the followingseen in the following videovideo and screen captures.and screen captures.

5. Part I: Hyperbolas center at thePart I: Hyperbolas center at the
origin.origin.
Example : In the first example the constant distance mentioned above will be
6, one focus will be at the point (0, 5) and the other will be at the point (0,
-5).The graph of a hyperbola with these foci and center at the origin is shown
below.
An equation of this hyperbola can be found by using the distance formula. We
calculate the distance from the point on the ellipse (x, y) to the two foci, (0, 5)
and (0, -5). This total distance is 6 in this example:

6. Note that 6 is the total distance from vertex to vertex through the center of this
hyperbola, shown by the dark red line on the graph. This is called the transverse axis.
After eliminating radicals and simplifying we have
If we let a = 4 and b = 3, this equation can be written as
. The important features are:
•b = 3, the distance from the center to the vertices of the hyperbola in
the vertical direction (up and down from the center). This is called the
transverse axis.
a = 4, and the two dotted lines in the graph are given by the
equations

7. is the distance from the center to each focus. Each focus is found on the
transverse axis.
The two dotted lines on the graph are asymptotes because the two
branches of the hyperbola approach but never reach these lines.
Sketching them first provides a good way to sketch the graph of a
hyperbola.