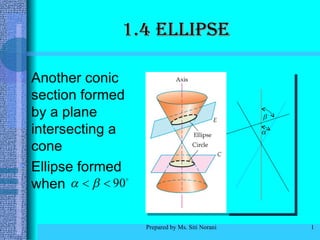
The document defines and provides properties of ellipses: - An ellipse is defined as the set of points where the sum of distances to two foci is a constant. - Examples provide the equations of ellipses given properties like the center, vertices, foci, major/minor axes. - Sketching examples illustrate key features like orientation and placement of ellipses.

1. 1.4 Ellipse Another conic section formed by a plane intersecting a cone Ellipse formed when

2. Definition: An ellipse is defined as the set of points in a plane such that the sum of the distances from P to two fixed points is a constant. The two fixed points are the foci.

3. Graph of an Ellipse Note various parts of an ellipse

4. The equation of an ellipse with centre (0,0) and foci x y c F 2 (-c.0) F 1 (c,0) V 2 (-a,o) V 1 (a,0) M 1 (0,b) M 2 (0,-b) G H J K

5. We summarized the properties of the ellipse with the horizontal major axis as, a > b >0 Vertices : Major axis : horizontal, length 2a Minor axis : vertical, length 2b Foci : where c 2 =a 2 -b 2 Latus rectum : vertical length

6. The equation of an ellipse with center (0,0) and foci x y c F 1 (0,c) F 2 (0,-c) V 2 (0,-b) V 1 (0,b) M 1 (0,a) M 2 (0,-a)

7. We summarised the properties of this second form of ellipse as follow:- b > a >0 Vertices : Major axis : vertical, length 2b Minor axis : horizontal, length 2a Foci where c 2 =b 2 -a 2 Latus rectum: vertical length

8. The equation of an ellipse with centre (h,k) and foci a > b >0 Vertices : Major axis : horizontal, length 2a Minor axis : vertical, length 2b Foci : where c 2 =a 2 -b 2 Latus rectum : vertical length

9. b > a >0 Vertices : Major axis : vertical, length 2b Minor axis : horizontal, length 2a Foci where c 2 =b 2 -a 2 Latus rectum: vertical length The equation of an ellipse with center (h,k) and foci

10. Example 1 Find the equation for the ellipse that has its centre at the origin with vertices V (0,± 7) and Foci ( 0,± 2 ). Solution The standard equation of an ellipse is where ;

11. Since the vertices are ( 0,± 7 ), we conclude that a = 7. Since the Foci are (0,±2), we have c = 2 . = 22 + 72 = 4 + 49 = 53 and equation of the ellipse is

12. Example 2 Find the equation for the ellipse that has its centre at the origin with vertices V (0,± 5) and minor axis of length 3. Sketch the ellipse. Solution The standard equation of an ellipse is where ; Since the vertices are ( 0,± 5 ), we conclude that b = 5. Since the minor axis is of length 3, we have

13. And equation of the ellipse is (0, 5) (0, – 5 ) 0 y x

14. Example 3 Find the focus and equation of the ellipse with centre (0,0) vertices at (2,0) and (0,4). Solution From the above and

15. Equation of ellipse is and Foci is ( 0, ) and

16. Example 4 Find the centre an vertices of the minor axis and the Foci of the ellipse . Solution The equation of an ellipse is For equation , , The centre of the ellipse is ; b = 2 , a = 3 .

17. Vertices of the minor axis are and Foci of the ellipse are and Since , c 2 = a 2 - b 2 = 9 – 4 = 5

18. Example 5 Write the equation of the ellipse that has vertices at and and Foci at and Solution The vertices and foci are on the same horizontal line . The equation of the ellipse is , Where a > b The centre of the ellipse is at the midpoint of the major axes

19. h = and k = The distance between the centre and vertex is 5 units ; thus . The distance between the centre ( 2,-5) and focus ( 5,-5) is 3 units, thus c = 3 , = = 16

20.  The equation of the ellipse is

21. Example 6 Find the equation of an ellipse with centre ( 3,1 ) and the major axis running parallel with the y axis. The length of the major axis is 10 units and the minor axis is 6 units. Sketch the ellipse.

22. Solution The equation for an ellipse with centre ( h,k ) and the major axis running parallel with the y axis is where ( b ² > a ² ) The length of the major axis is 10 units and the minor axis is 6 units. We get 2 b = 10 , 2 a = 6 b = 5 , a = 3

23. The equation of the ellipse is (3,6) (-3,-4) A . . y x F 1 ( 3,5) B F 2 ( -3,-3) D C ( 3,1) E .

24. Example 7 Find the equation of ellipse with vertices ( 8,5 ) and ( 10,1 ) with centre ( 8,k ). Solution Sketching the vertices of the ellipse given.

25. (10,1) (8,5) ( x,y ) ( x 1 , y 1 ) x y

26. We get the centre of ellipse is ( 8,1) , k = 1  x = 8, x 1 = 6, y 1 = 1 So equation of ellipse is +

27. Example 8 Sketch the graph of the equation, Solution: Complete the squares for the expressions 16( x 2 + 4 x +4 ) + 9( y 2 – 2 y + 1 ) = 71 + (16)(4) + (9)(1) 16 ( x + 2 ) 2 + 9 ( y – 1 ) 2 = 144

28. The equation is an ellipse with centre c ( -2,1) and a = 3, b = 4 c 2 = b 2 – a 2 = 16 – 9 = 7 c = ± Foci are

29. (-2,5) (1,1) (-5,1) (-2,1) x y Graph for equation