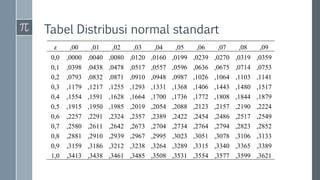
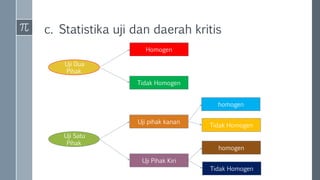
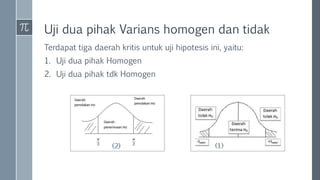
Dokumen tersebut membahas tentang uji hipotesis rata-rata, meliputi pengertian distribusi normal, mengapa distribusi normal penting, distribusi normal standar, standar deviasi, dan langkah-langkah uji hipotesis rata-rata termasuk rumusan hipotesis, tingkat signifikansi, statistik uji dan daerah kritis, serta menarik kesimpulan.

1. Uji Hipotesis Rata-rata
Angga Debby Frayudha
Pascasarjana Unnes
Jurusan Manajemen Pendidikan

2. Pengertian Distribusi Normal
Distribusi normal merupakan distribusi teoritis dari
variable random yang kontinu
Distribusi normal ini mula-mula diuraikan oleh
Abraham de Moivren dan dipopulerkan penggunannya oleh
Carl Fredreich Gauss dengan percobaannya. Oleh karena
itu, distribusi ini lebih dikenal dengan distribudi Gauss.

3. Mengapa Distribusi Normal Sangat Penting?
Distribusi normal memiliki beberapa sifat yang memungkinkan
untuk dipergunakan sebagai pedoman dalam menarik kesimpulan
berdasarkan hasil sampel.

4. Distribusi Normal Standar
› Karena distribusinya kontinu, cara menghitung probablitasnya dilakukan dengan
jalan menetukan luas di bawah kurvanya. Sayangnya, fungsi frekuensi normal tidak
memiliki integral yang sederhana sehingga probabilitas umumnya dihitung dengan
menggunakan distribusi normal standar dimana variabel randomnya ialah Z dengan µ = 0
dan σ = 1 sehingga variable normal standar dapat ditulis dengan rumus sebagai berikut:
Keterangan:
› Z : besarnya penyimpangan terhadap rata-rata.
› µ : rata-rata populasi.
› σ : standar deviasi.
› x : nilai variabel random.



x
z

5. Tabel Distribusi normal standart
z ,00 ,01 ,02 ,03 ,04 ,05 ,06 ,07 ,08 ,09
0,0 ,0000 ,0040 ,0080 ,0120 ,0160 ,0199 ,0239 ,0270 ,0319 ,0359
0,1 ,0398 ,0438 ,0478 ,0517 ,0557 ,0596 ,0636 ,0675 ,0714 ,0753
0,2 ,0793 ,0832 ,0871 ,0910 ,0948 ,0987 ,1026 ,1064 ,1103 ,1141
0,3 ,1179 ,1217 ,1255 ,1293 ,1331 ,1368 ,1406 ,1443 ,1480 ,1517
0,4 ,1554 ,1591 ,1628 ,1664 ,1700 ,1736 ,1772 ,1808 ,1844 ,1879
0,5 ,1915 ,1950 ,1985 ,2019 ,2054 ,2088 ,2123 ,2157 ,2190 ,2224
0,6 ,2257 ,2291 ,2324 ,2357 ,2389 ,2422 ,2454 ,2486 ,2517 ,2549
0,7 ,2580 ,2611 ,2642 ,2673 ,2704 ,2734 ,2764 ,2794 ,2823 ,2852
0,8 ,2881 ,2910 ,2939 ,2967 ,2995 ,3023 ,3051 ,3078 ,3106 ,3133
0,9 ,3159 ,3186 ,3212 ,3238 ,3264 ,3289 ,3315 ,3340 ,3365 ,3389
1,0 ,3413 ,3438 ,3461 ,3485 ,3508 ,3531 ,3554 ,3577 ,3599 ,3621

6. 2. Simpangan Baku atau Standar Deviasi ( S )
simpangan Baku adalah akar dari perbandingan antara jumlah kuadrat
simpangan-simpangan dengan banyaknya data.
Simpangan Baku Data Tunggal Biasa
Rumus : simpangan baku (s) =
› Keterangan :
› Xi = data ke-i atau nilai ke-i
› ͞x = rataan hitung
› n = banyaknya nilai data
› ∑ Ixi - ͞x I2 = Ix1 - ͞x I2 + Ix2 - ͞x I2 + Ix3 - ͞x I2 +...+ Ixn - ͞x I2
∑ I xi - ͞x I2
n

7. Contoh 1 :
› Tentukanlah simpangan baku ( S ) dari data : 4, 5, 6, 7,
3, 8, 2
› Penyelesaian :
› Untuk menentukan simpangan baku atau standar
deviasi ( S )
› dari data 4, 5, 6, 7, 3, 8, 2 perlu dicari dulu rataan
hitungnya ( ͞x ),
› yaitu :

8. Simpangan Baku atau Standar Deviasi ( S )Data
Tunggal dalam daftar Distribusi Frekuensi
Rumus :
› Simpangan Baku ( S ) =
› Keterangan :
› ͞x = rataan hitung atau mean
› xi = data ke – i
› ∑ fi = jumlah frekuensi
› ∑ fiI xi - ͞x I = f1 Ix1 - ͞x I + f2 Ix2 - ͞x I + f3 Ix3 - ͞x I +...+ fn Ixn - ͞x I
∑ fiI xi - ͞x I
∑ fi

9. 2.3. Simpangan Baku atau Standar Deviasi (S) Data
kelompok
› Simpangan Baku ( S ) =
› Keterangan :
› ͞x = rataan hitung atau mean
› xi = titik tengah kelas interval
› ∑ fi = jumlah frekuensi
› ∑ fiI xi - ͞x I2 = f1 Ix1 - ͞x I2 + f2 Ix2 - ͞x I2 + f3 Ix3 - ͞x I2 +...+ fn Ixn - ͞x I2
∑ fiI xi - ͞x I2
∑ fi

10. MAIN MENU

11. PENDAHULUAN
Tugas utama dari statistika inferensia adalah
melakukan pengujian hipotesis.
Pengujian hipotesis dilakukan sebagai upaya
memperoleh gambaran mengenai suatu
populasi dari sampel. Sehingga, informasi yang
diperoleh dari sampel digunakan untuk
menyusun suatu pendugaan terhadap nilai
parameter populasinya yang tidak diketahui.
MAIN MENU

12. PEMBAHASAN

13. LANGKAH-LANGKAH UJI HIPOTESIS DUA
RATA-RATA
a.Rumusan Hipotesis
b.Tingkat signifikasi
c.Statistik uji dan daerah
kritis
d.Menarik kesimpulan

14. Uji rata-rata
Uji nyata itu yang bagaimana ?
Uji sangat nyata itu yang bagaimana ?
Uji nyata/uji berarti/uji signifikan=0,05
Uji sangat nyata/uji sangat berarti/uji sangat signifikan=0,01

15. a. Rumusan Hipotesis
ada tiga kemungkinan cara menyusun hipotesis
nol dan alternatifnya, yaitu :
Menggunakan kriteria uji dua pihak
Menggunakan kriteria uji satu pihak kanan
Menggunakan kriteria uji satu pihak kiri

16. c. Statistika uji dan daerah kritis
Uji Dua
Pihak
Uji Satu
Pihak
Homogen
Tidak Homogen
Uji Pihak Kiri
Uji pihak kanan
homogen
Tidak Homogen
homogen
Tidak Homogen

17. 1. Uji Dua pihak
› 𝜎 diketahui 𝑧 =
𝑥−𝜇0
𝜎
𝑛

18. Uji dua pihak Varians homogen dan tidak
Terdapat tiga daerah kritis untuk uji hipotesis ini, yaitu:
1. Uji dua pihak Homogen
2. Uji dua pihak tdk Homogen

19. 2. Uji satu pihak
› varians homogen (standar deviasi populasi tidak
diketahui)
› varians tidak homogen (standar deviasi populasi
diketahui)

20. Pihak kiri
› 𝜎 𝑡𝑖𝑑𝑎𝑘 𝑑𝑖𝑘𝑒𝑡𝑎ℎ𝑢𝑖 =
› Tolak hipotesis 𝐻0 𝑗𝑖𝑘𝑎 𝑡 ≤ −𝑡1 −∝ 𝑑𝑒𝑛𝑔𝑎𝑛 𝑡1 −∝
𝑑𝑖𝑑𝑎𝑝𝑎𝑡 𝑑𝑟 𝑡 𝑠𝑡𝑢𝑑𝑒𝑛𝑡 𝑚𝑒𝑛𝑔𝑔𝑢𝑛𝑎𝑘𝑎𝑛 𝑝𝑒𝑙𝑢𝑎𝑛𝑔 1 −∝ 𝑑𝑎𝑛 𝑑𝑘 = (𝑛 − 1)
› 𝜎 𝑑𝑖𝑘𝑒𝑡𝑎ℎ𝑢𝑖 =
› Terima hipotesis 𝐻0 𝑗𝑖𝑘𝑎 − 𝑧 1
2 1 −∝ < 𝑧 < 𝑧 1
2 1 −∝ 𝑑𝑒𝑛𝑔𝑎𝑛 𝑧 1
2 (1 −

21. Uji satu pihak tidak homogen dan Homogen
Terdapat tiga daerah kritis untuk uji hipotesis ini, yaitu:
1. Uji satu pihak untuk pihak kanan homogen
2. Uji satu pihan untuk pihak kiri homogen

22. Uji satu pihak tidak homogen dan Homogen
Terdapat tiga daerah kritis untuk uji hipotesis ini, yaitu:
1. Uji satu pihak untuk pihak kanan tidak homogen
2. Uji satu pihan untuk pihak kiri tidak homogen

23. Varians homogen/tidak homogen
› Menentukan hipotesis nol (H0) dan hipotesis alternatif
(Ha)
› Menentukan taraf signifikasi
› Menentukan statistik yang cocok dan menentukan daerah
kritisnya
› Menghitung statistik uji
› Menarik kesimpulan.
MENU

24. CONTOH SOAL
seorang guru matematika mengikut sertakan
siswanya untuk mengikuti jam tambahan
pelajarannya. Dengan maksud agar pemahaman
siswanya akan pelajaran matematika
meningkat.Nilai siswa sebelum dan sesudah
mengikuti jam tambahan adalah sebagai berikut:
setelah : 75 66 98 81 72 65 67 77 91 78
sebelum:70 62 90 83 78 55 46 72 80 69
Diminta :
Ujilah bahwa dengan adanya jam tambahan
pelajaran matematika para siswa menjadi lebih
paham, pada
MAIN MENU

25. PENUTUP