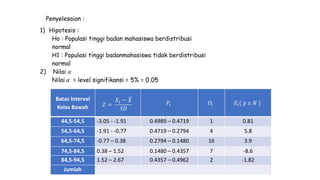
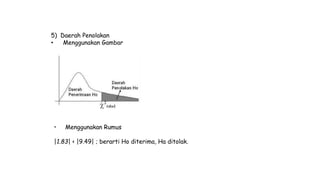
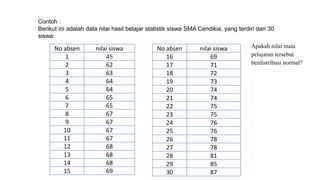
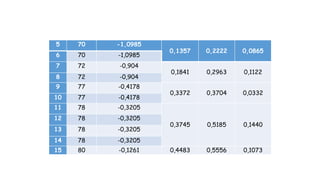
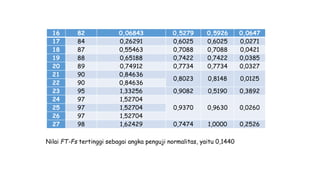
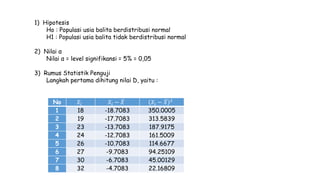
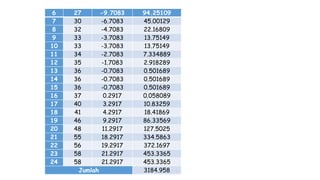
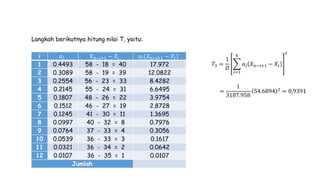
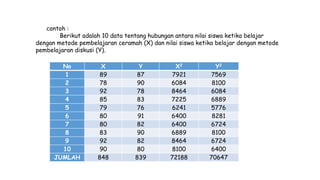
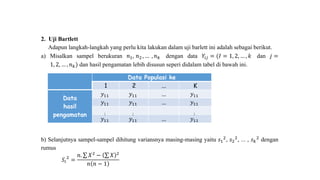
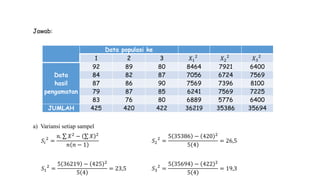
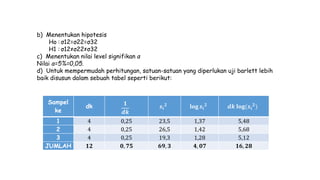
Dokumen ini membahas metodologi dan langkah-langkah dalam uji normalitas dan homogenitas data statistik menggunakan beberapa metode seperti Chi-square, Lilliefors, Kolmogorov-Smirnov, dan Shapiro-Wilk. Ujian dilakukan terhadap data tinggi badan dan berat badan untuk menentukan distribusi normalnya dengan berbagai hipotesis dan kriteria penolakan. Hasil menunjukkan bahwa data-data yang diuji, baik tinggi badan maupun berat badan, diterima sebagai berdistribusi normal pada tingkat signifikansi yang ditentukan.

1. UJI NORMALITAS DAN
HOMOGENITAS
OLEH
KELOMPOK 4
DENTI OKTAVIANI (06081181419065)
ENDAH RIZKIANI (06081181419026)
PUTRI HANDAYANI (06081181419018)

2. UJI NORMALITAS
1. Chi-Square
Chi-Square atau 𝑋2 untuk Uji Goodness of fit Distribusi Normal menggunakan
pendekatan penjumlahan penyimpangan data observasi tiap kelas dengan nilai yang
diharapkan
𝑋2
=
𝑂𝑖 − 𝐸𝑖
𝐸𝑖
Persyaratan Metode Chi-Square (Uji Goodness of fit Distribusi Normal) :
a) Data tersusun berkelompok atau dikelompokkan dalam table distribusi frekuensi.
b) Cocok untuk data dengan banyaknya angka besar ( n > 30 )
c) Setiap sel harus terisi, yang kurang dari 5 digabungkan.
Kriteria
Jika nilai 𝑋2
hitung < nilai 𝑋2
tabel, maka Ho diterima ; Ha ditolak.
Jika nilai 𝑋2
hitung > nilai 𝑋2
tabel, maka maka Ho ditolak ; Ha diterima.

3. Interval prestasi Frekuensi
45-54
55-64
65-74
75-84
85-94
1
4
16
7
2
Jumlah 30
Contoh :
Selidikilah apakah data tersebut di atas berdistribusi normal ? (Mean =71,2; Standar deviasi = 8,74)

4. Batas Interval
Kelas Bawah 𝑍 =
𝑋𝑖 − 𝑋
𝑆𝐷
𝑃𝑖 𝑂𝑖 𝐸𝑖( 𝑝 𝑥 𝑁 )
44,5-54,5 -3.05 - -1.91 0.4989 – 0.4719 1 0.81
54,5-64,5 -1.91 - -0.77 0.4719 – 0.2794 4 5.8
64,5-74,5 -0.77 – 0.38 0.2794 – 0.1480 16 3.9
74,5-84,5 0.38 – 1.52 0.1480 – 0.4357 7 -8.6
84,5-94,5 1.52 – 2.67 0.4357 – 0.4962 2 -1.82
Jumlah
Penyelesaian :
1) Hipotesis :
Ho : Populasi tinggi badan mahasiswa berdistribusi
normal
H1 : Populasi tinggi badanmahasiswa tidak berdistribusi
normal
2) Nilai 𝛼
Nilai 𝛼 = level signifikansi = 5% = 0,05

5. 3) Derajat Bebas
Df = ( k =panjang kelas) – 3 ) = ( 10 – 3 ) = 7
4) Nilai Tabel
Xtabel2=X1-∝,dk2=X(0.95,4)=9,49
𝑋2 =
(𝑂𝑖 − 𝐸𝑖)
𝐸𝑖
=
(1 − 0.81)2
0.81
+
(4 − 5.8)2
5.8
+
(16 − 3.9)2
3.9
+
(7 − (−8.6))2
−8.6
+
(2 − (−1.82))2
−1.82
= 1.83

6. 5) Daerah Penolakan
• Menggunakan Gambar
• Menggunakan Rumus
|1.83| < |9.49| ; berarti Ho diterima, Ha ditolak.

7. 2. Lilliefors
Metode Lilliefors menggunakan data dasar yang belum diolah dalam tabel
distribusi frekuensi. Data ditransformasikan dalam nilai Z untuk dapat dihitung
luasan kurva normal sebagai probabilitas komulatif normal.
𝑍𝑖 =
𝑋𝑖 − 𝑋
𝑠
Hipotesis dari uji Liliefors:
Ho : Sampel berdistribusi normal
Hi : Sampel tidak berdistribusi normal
Kriteria:
Jika Lhitung, < L tabel maka terima Ho dan tolak Hi
Jika Lhitung, > L tabel maka tolak Ho dan terima Hi

8. Contoh :
Berikut ini adalah data nilai hasil belajar statistik siswa SMA Cendikia, yang terdiri dari 30
siswa:
No absen nilai siswa
1 45
2 62
3 63
4 64
5 64
6 65
7 65
8 67
9 67
10 67
11 67
12 68
13 68
14 68
15 69
No absen nilai siswa
16 69
17 71
18 72
19 73
20 74
21 74
22 75
23 75
24 76
25 76
26 78
27 78
28 81
29 85
30 87
Apakah nilai mata
pelajaran tersebut
berdistribusi normal?

9. Penyelesaian :
Rata – rata
𝑥 =
Σ𝑥 𝑖
𝑛
=
2113
30
= 70,43
Standar Deviasi
𝑆𝐷 =
𝑥𝑖− 𝑥 2
𝑛−1
=
1835,367
29
= 63,28852 = 7,95
Kesimpulan :
Dari kolom terakhir dalam tabel di atas didapat L0 = 0,0188 dengan n = 30 dan
taraf nyata α = 0,05. Dari tabel Nilai Kritis L untuk Uji Liliefors di dapat L = 0,161 yang
lebih besar dari L0 = 0,0188 sehingga hipotesis H0 diterima.
Jadi data tersebut normal.

10. 3. Kolmogorov Smirnov
Metode Kolmogorov-Smirnov tidak jauh beda dengan metode Lilliefors. Langkah-
langkah penyelesaian dan penggunaan rumus sama, namun pada signifikansi yang
berbeda. Signifikansi metode Kolmogorov-Smirnov menggunakan tabel pembanding
Kolmogorov-Smirnov, sedangkan metode Lilliefors menggunakan tabel pembanding
metode Lilliefors.
No Xi
𝑍𝑖 =
𝑋𝑖 − 𝑋
𝑠
𝐹 𝑇 Fs 𝐹 𝑇 − 𝐹𝑠
1
2
3
4
dst

11. Persyaratan:
a. Data berskala interval atau ratio (kuantitatif)
b. Data tunggal / belum dikelompokkan pada tabel distribusi frekuensi
c. Dapat untuk n besar maupun n kecil.
Kriteria
Signifikansi uji, nilai |𝐹 𝑇 – Fs| terbesar dibandingkan dengan nilai tabel Kolmogorov
Smirnov.
 Jika nilai |𝐹 𝑇 – Fs| terbesar < nilai tabel Kolmogorov Smirnov, maka Ho diterima ; Ha
ditolak.
 Jika nilai |𝐹 𝑇 – Fs| terbesar > nilai tabel Kolmogorov Smirnov, maka Ho ditolak ; Ha
diterima.

12. Contoh :
Suatu penelitian tentang berat badan mahasiswa yang mengikuti pelatihan
kebugaran fisik/jasmani dengan sampel sebanyak 27 orang diambil secara
random, didapatkan data sebagai berikut ; 78, 78, 95, 90, 78, 80, 82, 77, 72,
84, 68, 67, 87, 78, 77, 88, 97, 89, 97, 98, 70, 72, 70, 69, 67, 90, 97 kg.
Selidikilah dengan α = 5%, apakah data tersebut di atas diambil dari populasi
yang berdistribusi normal ?

13. Penyelesaian:
1) Hipotesis
Ho : Populasi berat badan mahasiswa berdistribusi normal
H1 : Populasi berat badan mahasiswa tidak berdistribusi normal
2) Nilai α
Nilai α = level signifikansi = 5% = 0,05
No 𝑋𝑖
𝑍𝑖 =
𝑋𝑖 − 𝑋
𝑠
𝐹 𝑇 Fs 𝐹 𝑇 − 𝐹𝑠
1 67 -1,3902
0,0823 0,0741 0,0082
2 67 -1,3902
3 68 -1,2929 0,0985 0,1111 0,0126
4 69 -1,1957 0,1151 0,1481 0,0330

14. 5 70 -1,0985
0,1357 0,2222 0,0865
6 70 -1,0985
7 72 -0,904
0,1841 0,2963 0,1122
8 72 -0,904
9 77 -0,4178
0,3372 0,3704 0,0332
10 77 -0,4178
11 78 -0,3205
0,3745 0,5185 0,1440
12 78 -0,3205
13 78 -0,3205
14 78 -0,3205
15 80 -0,1261 0,4483 0,5556 0,1073

15. 16 82 0,06843 0,5279 0,5926 0,0647
17 84 0,26291 0,6025 0,6025 0,0271
18 87 0,55463 0,7088 0,7088 0,0421
19 88 0,65188 0,7422 0,7422 0,0385
20 89 0,74912 0,7734 0,7734 0,0327
21 90 0,84636
0,8023 0,8148 0,0125
22 90 0,84636
23 95 1,33256 0,9082 0,5190 0,3892
24 97 1,52704
0,9370 0,9630 0,026025 97 1,52704
26 97 1,52704
27 98 1,62429 0,7474 1,0000 0,2526
Nilai FT-Fs tertinggi sebagai angka penguji normalitas, yaitu 0,1440

16. 3) Derajat Bebas
Df tidak diperlukan.
4) Nilai Tabel
Nilai Kuantil Penguji Kolmogorov, α= 0,05 ; N = 27 ; yaitu 0,254. Tabel Kolmogorov Smirnov
pada lampiran.
5) Daerah Penolakan
Menggunakan rumus
| 0,1440 | < | 0,2540| ; berarti Ho diterima, Ha ditolak
6) Kesimpulan
Populasi tinggi badan mahasiswa berdistribusi normal α = 0,05.

17. 4. Shapiro Wilk
Metode Shapiro Wilk menggunakan data dasar yang belum diolah dalam tabel
distribusi frekuensi. Data diurut, kemudian dibagi dalam dua kelompok untuk
dikonversi dalamShapiro Wilk. Dapat juga dilanjutkan transformasi dalam nilai Z
untuk dapat dihitung luasan kurva normal.
𝑇3 =
1
𝐷
𝑖=1
𝑘
𝑎𝑖 𝑋 𝑛−𝑖+1 − 𝑋𝑖
2
𝐷 =
𝑖=1
𝑛
𝑋𝑖 − 𝑋 2 𝐺 = 𝑏 𝑛 + 𝑐 𝑛 + 𝑙𝑛
𝑇3 − 𝑑 𝑛
1 − 𝑇3
D = Berdasarkan rumus di bawah
ai = Koefisien test Shapiro Wilk
X n-i+1 = Angka ke n – i + 1 pada
data
X i = Angka ke i pada data
Xi = Angka ke i
pada data yang
ke-i
X = Rata-rata data
G = Identik dengan nilai Z
distribusi normal
T3 = Berdasarkan rumus di
atas
𝑏 𝑛, 𝑐 𝑛, 𝑑 𝑛 = Konversi Statistik
Shapiro-Wilk Pendekatan
Distribusi Normal (lampiran

18. Persyaratan
• Data berskala interval atau ratio (kuantitatif)
• Data tunggal / belum dikelompokkan pada tabel distribusi frekuensi
• Data dari sampel random
Signifikansi
Signifikansi dibandingkan dengan tabel Shapiro Wilk. Signifikansi uji nilai T3
dibandingkan dengan nilai tabel ShapiroWilk, untuk dilihat posisi nilai probabilitasnya
(p).
o Jika nilai p < 5%, maka Ho ditolak ; Ha diterima
o Jika nilai p > 5%, maka Ho diterima ; Ha ditolak.
Tabel Harga Quantil Statistik Shapiro-Wilk Distribusi Normal. Jika digunakan rumus
G, maka digunakan tabel 2 distribusi normal.

19. 1) Hipotesis
Ho : Populasi usia balita berdistribusi normal
H1 : Populasi usia balita tidak berdistribusi normal
2) Nilai α
Nilai α = level signifikansi = 5% = 0,05
3) Rumus Statistik Penguji
Langkah pertama dihitung nilai D, yaitu :
No 𝑋𝑖 𝑋𝑖 − 𝑋 𝑋𝑖 − 𝑋 2
1 18 -18.7083 350.0005
2 19 -17.7083 313.5839
3 23 -13.7083 187.9175
4 24 -12.7083 161.5009
5 26 -10.7083 114.6677
6 27 -9.7083 94.25109
7 30 -6.7083 45.00129
8 32 -4.7083 22.16809

20. 6 27 -9.7083 94.25109
7 30 -6.7083 45.00129
8 32 -4.7083 22.16809
9 33 -3.7083 13.75149
10 33 -3.7083 13.75149
11 34 -2.7083 7.334889
12 35 -1.7083 2.918289
13 36 -0.7083 0.501689
14 36 -0.7083 0.501689
15 36 -0.7083 0.501689
16 37 0.2917 0.058089
17 40 3.2917 10.83259
18 41 4.2917 18.41869
19 46 9.2917 86.33569
20 48 11.2917 127.5025
21 55 18.2917 334.5863
22 56 19.2917 372.1697
23 58 21.2917 453.3365
24 58 21.2917 453.3365
Jumlah 3184.958

21. i 𝑎𝑖 𝑋 𝑛−𝑖+1 − 𝑋𝑖 𝑎𝑖 𝑋 𝑛−𝑖+1 − 𝑋𝑖
1 0.4493 58 - 18 = 40 17.972
2 0.3089 58 - 19 = 39 12.0822
3 0.2554 56 - 23 = 33 8.4282
4 0.2145 55 - 24 = 31 6.6495
5 0.1807 48 - 26 = 22 3.9754
6 0.1512 46 - 27 = 19 2.8728
7 0.1245 41 - 30 = 11 1.3695
8 0.0997 40 - 32 = 8 0.7976
9 0.0764 37 - 33 = 4 0.3056
10 0.0539 36 - 33 = 3 0.1617
11 0.0321 36 - 34 = 2 0.0642
12 0.0107 36 - 35 = 1 0.0107
Jumlah
Langkah berikutnya hitung nilai T, yaitu:
𝑇3 =
1
𝐷
𝑖=1
𝑘
𝑎𝑖 𝑋 𝑛−𝑖+1 − 𝑋𝑖
2
=
1
3187.958
54.6894 2
= 0,9391

22. 4) Derajat Bebas
Db = n
5) Nilai Tabel
Pada lampiran dapat dilihat, nilai α (0,10) = 0,930 ; nilai α (0,50) = 0,963
6) Daerah Penolakan
Nilai T3 terletak diantara 0,930 dan 0,963, atau nilai p hitung terletak diantara 0,10 dan 0,50, yang
diatas nilai α (0,05) berarti Ho diterima, Ha ditolak
7) Kesimpulan
Sampel diambil dari populasi normal, pada α = 0,05. Cara lain setelah nilai T3 diketahui dapat
menggunakan rumus G, yaitu :
𝐺 = 𝑏 𝑛 + 𝑐 𝑛 + 𝑙𝑛
𝑇3 − 𝑑 𝑛
1 − 𝑇3
= 𝑏24 + 𝑐24 + 𝑙𝑛
𝑇3 − 𝑑24
1 − 𝑇3
= −5.605 + 1.862 + 𝑙𝑛
0.9391 − 0.2106
1 − 0.9391
= −1.2617

23. UJI HOMOGENITAS
1. Uji Homogenitas Variansi
Adapun langkah-langkah yang perlu kita lakukan dalam uji homogenitas variansi ini adalah sebagai
berikut.
a) Menentukan nilai varians/standar deviasi untuk variabel X dan Y, yaitu dengan rumus:
𝑆 𝑥
2
=
𝑛. 𝑋2 − 𝑋 2
)𝑛(𝑛 − 1
𝑆 𝑦
2
=
𝑛. 𝑌2 − 𝑌 2
)𝑛(𝑛 − 1
dengan: n = banyak data
b) Menentukan nilai 𝐹ℎ𝑖𝑡𝑢𝑛𝑔 dari varians X dan Y, yaitu dengan rumus:
𝐹 =
𝑆 𝑏𝑒𝑠𝑎𝑟
𝑆 𝑘𝑒𝑐𝑖𝑙

24. c) Menentukan hipotesis pengujian: Ho : 𝜎1
2
= 𝜎2
2
(varians data homogen)
Ha: 𝜎1
2
≠ 𝜎2
2
(varians data tidak homogen)
d) Menentukan level signifikan (𝛼)
𝛼 bernilai 0,01 atau bernilai 0,05.
e) Membandingkan 𝐹ℎ𝑖𝑡𝑢𝑛𝑔 dengan 𝐹𝑡𝑎𝑏𝑒𝑙 pada tabel distribusi F
Kriteria pengujian:
 jika: 𝐹ℎ𝑖𝑡𝑢𝑛𝑔 ≥ 𝐹 𝑡𝑎𝑏𝑒𝑙 𝛼;𝑑𝑘1;𝑑𝑘2 , maka Tolak Ho
 jika: 𝐹ℎ𝑖𝑡𝑢𝑛𝑔 < 𝐹 𝑡𝑎𝑏𝑒𝑙 𝛼;𝑑𝑘1;𝑑𝑘2 , maka Terima Ho
dimana: 𝑑𝑘 = (𝑛 − 1)

25. No X Y X2 Y2
1 89 87 7921 7569
2 78 90 6084 8100
3 92 78 8464 6084
4 85 83 7225 6889
5 79 76 6241 5776
6 80 91 6400 8281
7 80 82 6400 6724
8 83 90 6889 8100
9 92 82 8464 6724
10 90 80 8100 6400
JUMLAH 848 839 72188 70647
contoh :
Berikut adalah 10 data tentang hubungan antara nilai siswa ketika belajar
dengan metode pembelajaran ceramah (X) dan nilai siswa ketika belajar dengan metode
pembelajaran diskusi (Y).

26. Jawab:
a) Menentukan nilai varians/standar deviasi untuk variabel X dan Y, yaitu dengan rumus:
𝑆 𝑥
2
=
𝑛. 𝑋2 − 𝑋 2
𝑛 𝑛 − 1
=
10 72188 − 848 2
10 9
= 5,55
𝑆 𝑦
2
=
𝑛. 𝑌2 − 𝑌 2
𝑛(𝑛 − 1)
=
10 70647 − (839)2
10 (9)
= 5,32
b) Menentukan nilai 𝐹ℎ𝑖𝑡𝑢𝑛𝑔 dari varians X dan Y, yaitu dengan rumus:
Dari perhitungan di atas didapat, 𝑆 𝑥 > 𝑆 𝑦
𝐹 =
𝑆 𝑏𝑒𝑠𝑎𝑟
𝑆 𝑘𝑒𝑐𝑖𝑙
=
5,55
5,32
= 1,04
Dari perhitungan diatas, 𝐹ℎ𝑖𝑡𝑢𝑛𝑔 = 1,04 dan grafik daftar distribusi F dengan dk pembilang
= 10 – 1 = 9. dk penyebut = 10 – 1 = 9. Dan 𝛼 = 0,05 dan 𝐹𝑡𝑎𝑏𝑒𝑙 = 3,18
Tampak bahwa 𝐹ℎ𝑖𝑡𝑢𝑛𝑔 < 𝐹𝑡𝑎𝑏𝑒𝑙. Hal ini berarti data variabel X dan Y homogen.

27. 2. Uji Bartlett
Adapun langkah-langkah yang perlu kita lakukan dalam uji barlett ini adalah sebagai berikut.
a) Misalkan sampel berukuran 𝑛1, 𝑛2 , … , 𝑛 𝑘 dengan data 𝑌𝑖𝑗 = (𝐼 = 1, 2, … , 𝑘 dan 𝑗 =
1, 2, … , 𝑛 𝑘) dan hasil pengamatan lebih disusun seperi didalam tabel di bawah ini.
Data Populasi ke
1 2 ... K
Data
hasil
pengamatan
𝑦11 𝑦11 ... 𝑦11
𝑦11 𝑦11 ... 𝑦11
⋮ ⋮ ⋮
𝑦11 𝑦11 ... 𝑦11
b) Selanjutnya sampel-sampel dihitung variansnya masing-masing yaitu 𝑠1
2, 𝑠2
2, ... , 𝑠 𝑘
2 dengan
rumus
𝑆𝑖
2
=
𝑛. 𝑋2
− 𝑋 2
𝑛 𝑛 − 1

28. Sampel
ke
dk 𝟏
𝒅𝒌
𝒔𝒊
𝟐
𝐥𝐨𝐠 𝒔𝒊
𝟐
𝒅𝒌 𝐥𝐨𝐠(𝒔𝒊
𝟐
)
1 𝑛1 − 1 1/(𝑛1 − 1) 𝑠1
2 log 𝑠1
2 (𝑛1−1) log(𝑠1
2)
2 𝑛2 − 1 1/(𝑛2 − 1) 𝑠2
2
log 𝑠2
2
(𝑛2−1) log(𝑠2
2
)
⋮ ⋮ ⋮ ⋮ ⋮
k 𝑛 𝑘 − 1 1/(𝑛 𝑘 − 1) 𝑠 𝑘
2
log 𝑠 𝑘
2
(𝑛 𝑘−1) log(𝑠 𝑘
2
)
c) Untuk mempermudah perhitungan, satuan-satuan yang diperlukan uji barlett lebih baik
disusun dalam sebuah tabel seperti berikut:
d) Menentukan hipotesis
Ho : σ12=σ22=… =σk2
H1 : σ12≠σ22≠… ≠σk2

29. e) Menentukan nilai level signifikan 𝛼
𝛼 bernilai 0,01 atau bernilai 0,05.
f) Menghitung nilai-nilai statistik penguji, sebagai berikut:
 Varians gabungan dari semua sampel
𝑠2 =
𝑛𝑖 − 1)𝑠𝑖
2
𝑛 − 1
 Harga satuan B
𝐵 = log 𝑠2
𝑛𝑖 − 1
 Statistik chi-kuadrat
𝑋2 = (ln 10) 𝐵 − 𝑛 − 1 log 𝑠𝑖
2
dengan ln 10 = 2,3026

30. g) Membandingkan 𝑋2
ℎ𝑖𝑡𝑢𝑛𝑔 dengan 𝑋2
𝑡𝑎𝑏𝑒𝑙 pada tabel distribusi chi-square
Kriteria pengujian: jika: 𝑋2
ℎ𝑖𝑡𝑢𝑛𝑔 ≥ 𝑋2
𝑡𝑎𝑏𝑒𝑙(1−𝛼)(𝑘−1) , maka Tolak Ho
jika: 𝑋2
ℎ𝑖𝑡𝑢𝑛𝑔 < 𝑋2
𝑡𝑎𝑏𝑒𝑙(1−𝛼)(𝑘−1) , maka Terima Ho
dimana jika 𝑋2
𝑡𝑎𝑏𝑒𝑙 1−𝛼 𝑘−1 didapatkan dari tabel distribusi chi-square dengan
peluang 1 − 𝛼 dan 𝑑𝑘 = 𝑘 − 1
Contoh:
Berikut adalah data nilai siswa ketika diajarkan dengan tiga strategi pembelajaran
(ekpositori, inkuiri, dan konstektual) yang berbeda.
Data populasi ke
1 2 3
Data
hasil
pengamatan
92 89 80
84 82 87
87 86 90
79 87 85
83 76 80

31. Data populasi ke
1 2 3 𝑋1
2
𝑋2
2
𝑋3
2
Data
hasil
pengamatan
92 89 80 8464 7921 6400
84 82 87 7056 6724 7569
87 86 90 7569 7396 8100
79 87 85 6241 7569 7225
83 76 80 6889 5776 6400
JUMLAH 425 420 422 36219 35386 35694
Jawab:
a) Variansi setiap sampel
𝑆𝑖
2
=
𝑛. 𝑋2
− 𝑋 2
𝑛 𝑛 − 1
𝑆1
2
=
5 36219 − 425 2
5 4
= 23,5
𝑆2
2
=
5 35386 − 420 2
5 4
= 26,5
𝑆3
2
=
5 35694 − 422 2
5 4
= 19,3

32. Sampel
ke
dk 𝟏
𝒅𝒌
𝒔𝒊
𝟐 𝐥𝐨𝐠 𝒔𝒊
𝟐 𝒅𝒌 𝐥𝐨𝐠(𝒔𝒊
𝟐)
1 4 0,25 23,5 1,37 5,48
2 4 0,25 26,5 1,42 5,68
3 4 0,25 19,3 1,28 5,12
JUMLAH 𝟏𝟐 𝟎, 𝟕𝟓 𝟔𝟗, 𝟑 𝟒, 𝟎𝟕 𝟏𝟔, 𝟐𝟖
b) Menentukan hipotesis
Ho : σ12=σ22=σ32
H1 : σ12≠σ22≠σ32
c) Menentukan nilai level signifikan α
Nilai α=5%=0,05.
d) Untuk mempermudah perhitungan, satuan-satuan yang diperlukan uji barlett lebih
baik disusun dalam sebuah tabel seperti berikut:

33. e) Menghitung nilai-nilai statistik penguji, sebagai berikut:
 Varians gabungan dari semua sampel
𝑠2
=
𝑛𝑖 − 1)𝑠𝑖
2
𝑛 − 1
=
)4 23,5 + 4 26,5 + 4(19,3
4 + 4 + 4
= 23,1
Sehingga log 𝑠2 = log 23,1 = 1,36
 Harga satuan B
𝐵 = log 𝑠2
𝑛𝑖 − 1 = 1,36 12 = 16,32
 Statistik chi-kuadrat
𝑋2 = ln 10 𝐵 − 𝑛 − 1 log 𝑠𝑖
2 = 2,3026 16,32 − 16,28 = 0,0921

34. f) Membandingkan 𝑋2
ℎ𝑖𝑡𝑢𝑛𝑔 dengan 𝑋2
𝑡𝑎𝑏𝑒𝑙 pada tabel distribusi chi-square
Kriteria pengujian:
jika: 𝑋2
ℎ𝑖𝑡𝑢𝑛𝑔 ≥ 𝑋2
𝑡𝑎𝑏𝑒𝑙(1−𝛼)(𝑘−1) , maka Tolak Ho
jika: 𝑋2
ℎ𝑖𝑡𝑢𝑛𝑔 < 𝑋2
𝑡𝑎𝑏𝑒𝑙(1−𝛼)(𝑘−1) , maka Terima Ho
𝑑𝑘 = 4 ;
jika 𝛼 = 5% dari tabel distribusi chi-square dengan 𝑑𝑘 = 4 didapat 𝑋2
𝑡𝑎𝑏𝑒𝑙(0,95)(4) = 9,48
Tampak bahwa 𝑋2
ℎ𝑖𝑡𝑢𝑛𝑔 < 𝑋2
𝑡𝑎𝑏𝑒𝑙. Hal ini berarti data tersebut homogen.