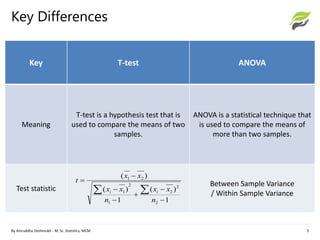
T-test and ANOVA are statistical techniques used to test hypotheses and compare population means. The t-test is used to compare the means of two samples or groups, while ANOVA can compare the means of more than two groups. Specifically, the t-test examines whether two sample means are significantly different and assumes a normal distribution and unknown standard deviation. ANOVA compares three or more population means by assessing variation within and between groups, and assumes samples are from normally distributed populations with equal variances. Researchers should use a t-test when comparing only two means and ANOVA when comparing more than two means to avoid increasing the chances of a Type I error.

1. T-test vs ANOVA
By: Aniruddha Deshmukh – M. Sc. Statistics, MCM

2. Background
By Aniruddha Deshmukh - M. Sc. Statistics, MCM 2
Ref: my earlier post on “Data Types”
• t-test and Analysis of Variance abbreviated as ANOVA, are
two parametric statistical techniques used to test the
hypothesis.
• Both are based on the common assumption like the
population from which sample is drawn should be normally
distributed, people often misinterpret these two.
• There is a very thin line of separation between t-test and
ANOVA, i.e. when the population means of only two groups
is to be compared, the t-test is used, but when means of
more than two groups are to be compared, ANOVA is used.

3. T-test
• t-test examines whether the population means of two samples greatly
differ from one another or not.
• Used when the standard deviation is not known, and the sample size is
small.
• It is a tool to analyse whether the two samples are drawn from the same
population.
• The test is based on t-statistic, which assumes that variable is normally
distributed (symmetric bell-shaped distribution) and mean is known and
population variance is calculated from the sample.
• The null hypothesis takes the form of H0: µ(x) = µ(y) against alternative
hypothesis H1: µ(x) ≠ µ(y), wherein µ(x) and µ(y) represents the
population means. The degree of freedom of t-test is n1 + n2 – 2
By Aniruddha Deshmukh - M. Sc. Statistics, MCM 3

4. Analysis of Variance (ANOVA)
By Aniruddha Deshmukh - M. Sc. Statistics, MCM 4
• ANOVA is used when the comparison is to be made between
more than two population means such as manufacturing defects
from different shifts or from different process or from difference
plants.
• When we use ANOVA, it is assumed that the sample is drawn
from the normally distributed population and the population
variance is equal.
• The basic principle is to test the variances among population
means by assessing the amount of variation within group items,
proportionate to the amount of variation between groups.
• The null hypothesis takes the form of H0: all population means are
the same and alternative hypothesis H1: at least one population
mean is different.

5. Key Differences
By Aniruddha Deshmukh - M. Sc. Statistics, MCM 5
Key T-test ANOVA
Meaning
T-test is a hypothesis test that is
used to compare the means of two
samples.
ANOVA is a statistical technique that
is used to compare the means of
more than two samples.
Test statistic
Between Sample Variance
/ Within Sample Variance
1
)(
1
)(
)(
2
2
2
1
2
1
21








n
xx
n
xx
xx
t
ii

6. Summary
By Aniruddha Deshmukh - M. Sc. Statistics, MCM 6
• When we have only two samples to be compared for their
means – use t-test
• Two-sample t-tests are problematic, if we need to compare
more than two samples?
– Increasing chance of committing a statistical type I error.
– As the number of t-tests increases, the number of two sample t-tests
also increases.
– So more the t-tests you run, the greater the risk of a type I error
(rejecting the null when there is no difference)
• When we have more than two samples to be compared for
their means – use ANOVA

7. Aniruddha Deshmukh – M. Sc. Statistics, MCM
email: annied23@gmail.com
For more information please contact: