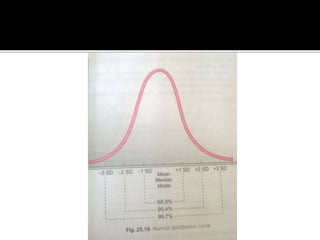
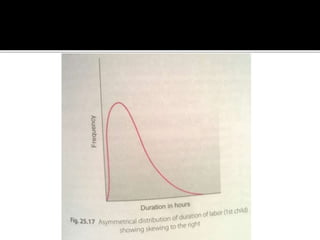
The document explains the null hypothesis, which posits no difference or effect, and details the process for testing it using statistical significance, including the role of p-values. It also describes normal distribution and skewed distributions, elaborating on the calculation of probabilities using addition and multiplication rules, especially in the context of independent and mutually exclusive events. Additionally, examples are provided to illustrate the calculation of probabilities in various scenarios.

2.  NULL HYPOTHESIS simply means “ NO
DIFFERENCE”
 The hypothesis says that OBSERVED
DIFFERENCE IS ENTIRELY DUETO
SAMPLING ERROR i.e. it occurred purely by
chance.
 It is denoted by Ho.

3. In the test of significance ,null hypothesis is
postulated to establish the basis for
calculating the probability that the difference
occurred purely of chance.

4. i. A NULL HYPOTHESIS ,suitable to problem
is set up
ii. An alternate hypothesis is defined, if
necessary.
iii. A suitable statistical test, using a relevant
formula is calculated.
iv. The DEGREE OF FREEDOM is determined.

5. v.Then the probability value (p value) is found
out, corresponding to the calculated value of
test and its degree of freedom
vi. If ‘p value’ is less than 0.05 - test is NOT
SIGNIFICANT.
vii. If ‘p value’ is more than 0.05- test is
SIGNIFICANT

6. TEST OF SIGNIFICANCE:
 When the difference is significant-Null
hypothesis is REJECTED
 When the difference is not significant-Null
hypothesis is NOT REJECTED i.e. approved.

7.  The null hypothesis is never proved to be
completely right or wrong, or true or false.
 But it is only REJECTED or NOT REJECTED at
the probability level of significance
concerned.

8.  Technical null hypotheses are used to verify statistical
assumptions.
 Scientific null assumptions are used to directly advance
a theory. i.e. to approve it.
 Null hypotheses of homogeneity are used to verify that
multiple experiments are producing consistent result
.
 It asserts the equality of effect of two or more
alternative treatments, for example, a drug and a
placebo, are used to reduce scientific claims based on
statistical noise.This is the most popular null
hypothesis; It is so popular that many statements about
significant testing assume such null hypotheses.

9. It is defined as the prediction that there is a
measurable interaction between variables
It is also called as “MANTAINED
hypothesis” or “RESEARCH hypothesis”
It is denoted by H(a)
Null hypothesis is opposed by alternative
hypothesis.
When null hypothesis is rejected,
ALTERNATIVE HYPOTHESIS is not rejected
and vice versa.

10. NORMAL
DISTRIBUTION
CURVE

11.  Normal distribution is an arrangement of a
data set in which most values cluster in the
middle of the range and the rest taper off
symmetrically toward either extreme.

13.  Area under the curve can be represented in
terms of relationship between and the
standard deviation .The relationship is
expressed as follows:
a) Mean +or- 1SD includes 68.3% of all
observations.
b) Mean + or -2SD includes 94.4% of all
observations.
c) Mean + or – 3 SD includes 99.7% of all
observations.

14. i. NDC has a peak in the centre with two tails
on either side.
ii. The mean, median and mode of the
distribution coincide and correspond to the
peak of the distribution
iii. The curve is bell shaped and bilaterally
symmetrical around the mean of the
distribution

15. iv.The proportion of frequencies lying on either
side of mean follows a specific type of
pattern.
v.The area under normal curve is unity or one.
vi. Standard deviation is one.

16.  When the frequency distribution or a
frequency curve is not symmetrical about the
peak , it is said to be SKEWED
DISTRIBUTION.
 In this one tail of the curve will be longer then
the other.
 This skewness can be either to the left or to
thev right of the peak.

18. THE average relative frequency with which an
event is expected to occur in the given
population or universe.
 It is denoted by “P”

19. It ranges from 0 to 1.
Zero is the minimum value –It represent
absolute impossibility of occurrence of an
event.
One is the maximum value - It represents
absolute certainty of occurrence all the times.

20.  IT CAN BE CALCULATEDAS
P=n(p)/N
WHERE , n(p) =no. of times
the event occurred.
N= total no. of trials

21.  Eg : probability of getting kings in a set of
playing cards – 4/52 = 1/13

22. To find out probabilities in complex situation
where the same event is happening in more
than one ways and events concerned or
independent, 2 rules are present-
i) ADDITION RULE
ii) MULTIPLICATION RULE

23.  If an event is occuring in mutually exclusive
way in trial then the total probability of
occurrence of that event in any way of trial is
the sum of probabilities of the occurrence of
that event in individual trial .
 Mutual exclusive events –events that cannot
occur simultaneously or present at same
time.They follow this rule.

24. FORMULA :
P ( A or B)=P (A) + P(B)
where A and B are
mutualy exclusive

25.  Eg : what is the Probability of getting red or
green colour balls from a set of 20 balls?
 5 balls of each colour – red ,green ,blue and
yellow respectively
 Probability of getting red balls - 5/20 = 1/4
 Probability of getting green balls - 5/20 = 1/4
 Then total probability = sum of individual
probabilities= ¼ + 1/4 = 2/4 = 1/2

26.  Independent events follow the multiplication
rule of probability.
 INDEPENDENT EVENTS :Two events are
said to be independent ,if the absence or
presence of one does not alter the chances of
other being present, or if the occurrence of
one does not alter the chance of occurrence
of other.

27. MULTIPLICATION RULE:
P(A & B)=P(A)*P(B)
ifA and B are independent events.

28.  Eg : what will be the probability of child being
male and Rh negative?
 Probability of a child born being male =P(1) =
1/2
 Probability of child born being Rh negative =
P(2) = 1/10 {10% children at birth may be
Rh negative}

29.  Probability of child being male and Rh
negative
= P(1) * P(2)
= 1/2 * 1/10
= 1/20 = 0.05

30. THANK YOU