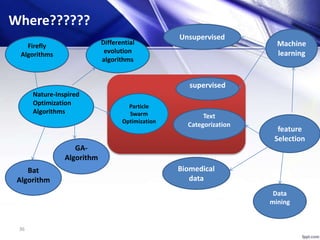
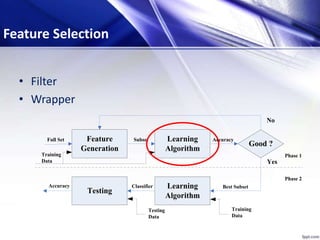
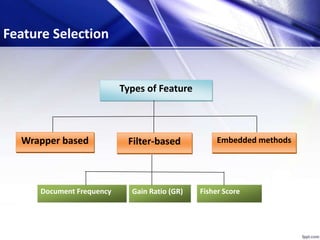
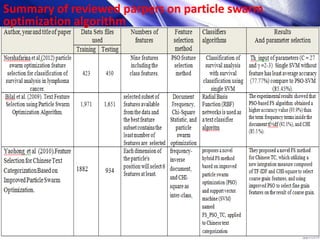
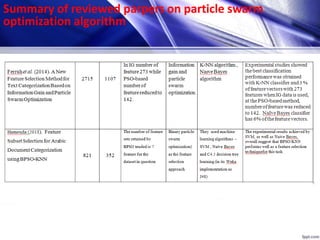
This document discusses using particle swarm optimization (PSO) for feature selection in text categorization. It provides an introduction to PSO, explaining how it was inspired by bird flocking behavior. The document outlines the PSO algorithm, parameters, and concepts like particle velocity and position updating. It also discusses feature selection techniques like filter and wrapper methods and compares different feature utility measures that can be used.

1. YAHYE ABUKAR AHMED
Supervisor: Yrd. Doç.Dr. MUSTAFA SERVET KIRAN
FEUTURE SELECTION
USING PARTICLE SWARM
OPTIMIZATION (PSO)
Date: 16 /12/ 2015

2. Presentation outline
1.0 • Introduction
2.0 • Concept of PSO
3.0 • Literature Review
4.0
• PSO Algorithm-Parameter Selection
5.0
• DWC’s application
6.0
• Summary of reviewed paper7.0
• Implementing PSO on the Text

3.  A group of birds are randomly
searching food in an area. There is only
one piece of food in the area being
searched.
 All the birds do not know where the
food is. But they know how far the
food is in each iteration.
 So what's the best strategy to find the
food?????????????????????
 The effective one is to follow the bird
which is nearest to the food.
Problem Definition
Suppose the following scenario:

4. optimization of continuous nonlinear functions
↓
finding the best solution in problem space
Problem Definition

5. 5
 Developed by James
Kennedy((social-psychologist),
Bureau of Labor Statistics, U.S.
Department of Labor.
 and Russ Eberhart (electrical
engineer), Purdue University at
1995.
Origins and Inspiration from Natural Systems
INTRODCUTION

6. • PSO is a robust stochastic optimization technique based
on the movement and intelligence of swarms.
• PSO applies the concept of social interaction to problem
solving.
• It uses a number of agents (particles) that constitute a
swarm moving around in the search space looking for the
best solution.
• Each particle is treated as a point in a N-dimensional space
which adjusts its “flying” according to its own flying
experience as well as the flying experience of other
particles.
What is Particle Swarm Optimization (PSO)?
INTRODCUTION

7. • Each solution is considered as bird, called particle
All the particles have a fitness value.
• The fitness values can be calculated using objective
function.
• All the particles preserve their individual best performance
They also know the best performance of their group
They adjust their velocity considering their best
performance and also considering the best performance of
the best particle
What is Particle Swarm Optimization (PSO)?
INTRODCUTION

8. • Each particle keeps track of its coordinates in the
solution space which are associated with the best
solution (fitness) that has achieved so far by that
particle. This value is called personal best , pbest.
• Another best value that is tracked by the PSO is the
best value obtained so far by any particle in the
neighborhood of that particle. This value is called
gbest.
• The basic concept of PSO lies in accelerating each
particle toward its pbest and the gbest locations, with
a random weighted accelaration at each time step as
shown in Fig.1
INTRODCUTION
What is Particle Swarm Optimization (PSO)?

9. Fig.1 Concept of modification of a searching point by PSO
sk : current searching point.
sk+1: modified searching point.
vk: current velocity.
vk+1: modified velocity.
vpbest : velocity based on pbest.
vgbest : velocity based on gbest
sk
vk
vpbest
vgbest
sk+1
vk+1
sk
vk
vpbest
vgbest
sk+1
vk+1
x
y
CONCEPT OF PSO

10. • Each particle tries to modify its position
using the following
information:
 the current positions,
 the current velocities,
 the distance between the current position and pbest,
 the distance between the current position and the gbest.
CONCEPT OF PSO

11. • The modification of the particle’s position can be
mathematically
• modeled according the following equation :
• Vi
k+1 = wVi
k +c1 rand1(…) x (pbesti-si
k) + c2 rand2(…) x
(gbest-si
k) ….. (1)
• where, vi
k : velocity of agent i at iteration k,
w: weighting function,
cj : weighting factor,
rand : uniformly distributed random number between 0 and 1,
si
k : current position of agent i at iteration k,
pbesti : pbest of agent i,
gbest: gbest of the group.
CONCEPT OF PSO

12. The following weighting function is usually utilized in (1)
w = wMax-[(wMax-wMin) x iter]/maxIter (2)
where wMax= initial weight,
wMin = final weight,
maxIter = maximum iteration number,
iter = current iteration number.
si
k+1 = si
k + Vi
k+1 (3)
CONCEPT OF PSO

13. A large inertia weight (w) facilitates a global search while
a small inertia weight facilitates a local search.
By linearly decreasing the inertia weight from a relatively
large value to a small value through the course of the
PSO run gives the best PSO performance compared
with fixed inertia weight settings.
Larger w ----------- greater global search ability
Smaller w ------------ greater local search ability.
Inertial weight factor

14. Flow chart depicting
the General PSO Algorithm:
Start
Initialize particles with random position
and velocity vectors.
For each particle’s position (p)
evaluate fitness
If fitness(p) better than
fitness(pbest) then pbest= p
Loopuntilall
particlesexhaust
Set best of pBests as gBest
Update particles velocity (eq. 1) and
position (eq. 3)
Loopuntilmaxiter
Stop: giving gBest, optimal solution.

15. Particles Adjust their positions according to a ``Psychosocial
compromise’’ between what an individual is comfortable with, and
what society reckons
Here I
am!
The best
perf. of my
neighbours
My best
performance
x
pg
pi
v
How It Works

16. Example

17. Example

18. Example

19. Example

20. Example

21. Example

22. Example

23. Example

24.  Algorithm parameters
– A : Population of agentspi : Position of agent ai in the solution space
– pi : Position of agent ai in the solution space
– f : Objective function
– vi : Velocity of agent’s ai
– V(ai) : Neighborhood of agent ai (fixed)
 The neighborhood concept in PSO is not the same as the one
used in other meta-heuristics search, since in PSO each
particle’s neighborhood never changes (is fixed)
Algorithm - Parameters

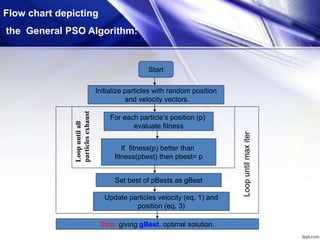
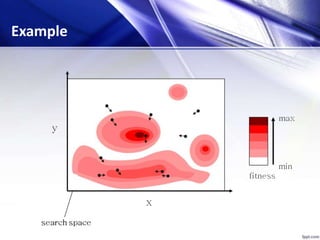
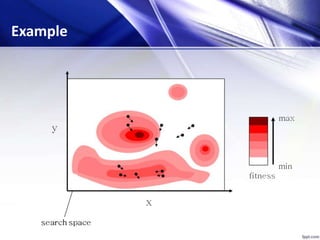
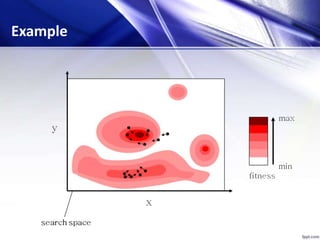
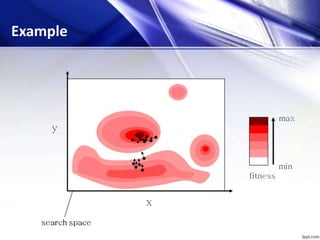
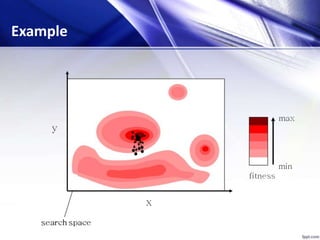
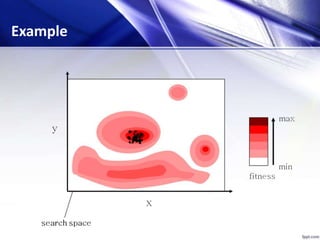
25. [x*] = PSO()
P = Particle_Initialization();
For i=1 to it_max
For each particle p in P do
fp = f(p);
If fp is better than f(pBest)
pBest = p;
end
end
gBest = best p in P;
For each particle p in P do
v = v + c1*rand*(pBest – p) + c2*rand*(gBest – p);
p = p + v;
end
end
Algorithm - Parameters

26.  Particle update rule
p = p + v
 with
v = v + c1 * rand * (pBest – p) + c2 * rand * (gBest – p)
 where
• p: particle’s position
• v: path direction
• c1: weight of local information
• c2: weight of global information
• pBest: best position of the particle
• gBest: best position of the swarm
• rand: random variable
Algorithm - Parameters

27. Nebojša Trpković
trx.lists@gmail.com
Slide 27 of 18
Single Particle

28.  Number of particles usually between 10 and 50
 C1 is the importance of personal best value
 C2 is the importance of neighborhood best value
 Usually C1 + C2 = 4 (empirically chosen value)
 If velocity is too low → algorithm too slow
 If velocity is too high → algorithm too unstable
 Cognitive coefficient c1 and social coefficient c2 are constants
known as acceleration coefficients,
Algorithm - Parameters

29. 1. Create a ‘population’ of agents (particles) uniformly distributed
over X
2. Evaluate each particle’s position according to the objective
function
3. If a particle’s current position is better than its previous best
position, update it
4. Determine the best particle (according to the particle’s previous
best positions)
Algorithm - Parameters

30. 5. Update particles’ velocities:
6. Move particles to their new positions:
7. Go to step 2 until stopping criteria are satisfied
Algorithm - Parameters

31. Particle’s velocity:
• Makes the particle move in the same
direction and with the same velocity
1. Inertia
2. Personal
Influence
3. Social
Influence
• Improves the individual
• Makes the particle return to a previous
position, better than the current
• Conservative
• Makes the particle follow the best
neighbors direction
Algorithm - Parameters

32.  Intensification: explores the previous solutions, finds the best
solution of a given region
 Diversification: searches new solutions, finds the regions with
potentially the best solutions
 In PSO:
Algorithm - Parameters

33. • Number of particles (swarmsize)
• C1 (importance of personal best)
• C2 (importance of neighbourhood best)
• Vmax: limit on velocity
• c1, c2 are learning factors
DWC’s Parameters

34. Play with DWC’s app for a while

35. TEXT FEATURE SELECTION
USING
PARTICLE SWARM OPTIMIZATION

36. 36
Machine
learning
Unsupervised
supervised
Nature-Inspired
Optimization
Algorithms
GA-
Algorithm
Differential
evolution
algorithms
Particle
Swarm
Optimization
Firefly
Algorithms
Bat
Algorithm
feature
Selection
Biomedical
data
Data
mining
Text
Categorization
Where??????

37. • Feature selection is used to identify a powerfully
predictive subset of fields within the database and to
reduce the number of fields presented to the mining
process.
• Affects several aspects of pattern classification:
1.The accuracy of classification algorithm learned
2.The time needed for learning a classification
function
3.The number of examples needed for learning
4.The cost associated with feature
Feature Selection

38. • Filter
• Wrapper
Feature
Generation
Learning
Algorithm
Testing
Learning
Algorithm
Good ?
Phase 1
Phase 2
Subset
Classifier Best Subset
Training
Data
Training
Data
Testing
Data
Accuracy
Yes
No
AccuracyFull Set
Feature Selection

39. 39
In text classification, we usually represent documents in a
high-dimensional space, with each dimension corresponding to
a term.
In this lecture: axis = dimension = word = term = feature
Many dimensions correspond to rare words.
Rare words can mislead the classifier.
Rare misleading features are called noise features.
Eliminating noise features from the representation increases
efficiency and effectiveness of text classification.
Eliminating features is called feature selection.
Feature Selection

40. Types of Feature
Document Frequency Gain Ratio (GR) Fisher Score
Filter-basedWrapper based Embedded methods
Feature Selection

41. 41
 A feature selection method is mainly defined by the
feature utility measure it employs
Feature utility measures:
Frequency – select the most frequent terms
Mutual information – select the terms with the highest
mutual information
Mutual information is also called information gain in
this context.
Chi-square
Document Frequency (DF)
Different feature selection
methods

42. Methods used in the reviewed
papers
The paper of Ferruh which about A New Feature Selection Method For Text
Categorization Based On Information Gain And Particle Swarm
Optimization

43. Summary of reviewed parpers on particle swarm
optimization algorithm

44. Summary of reviewed parpers on particle swarm
optimization algorithm

45. THANKS