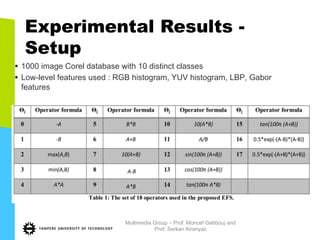
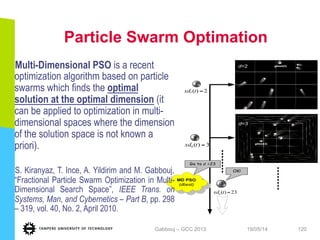
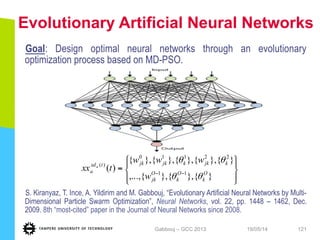
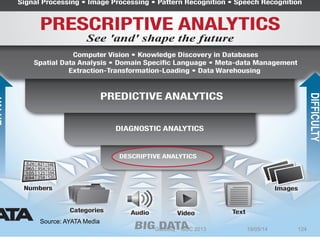
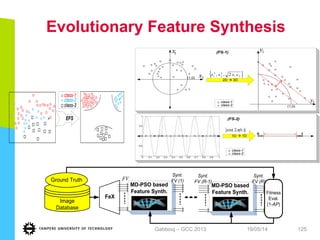
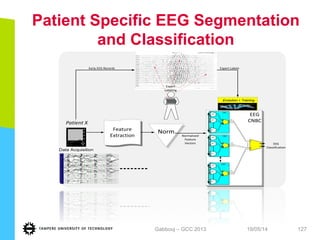
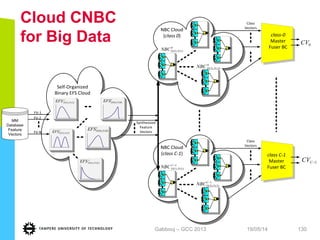
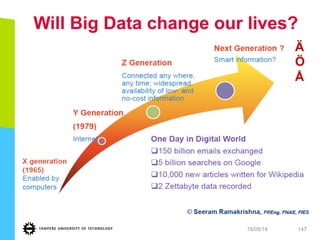
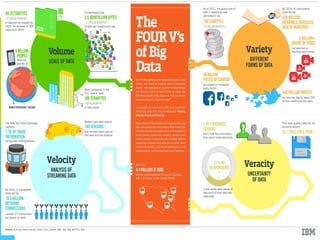
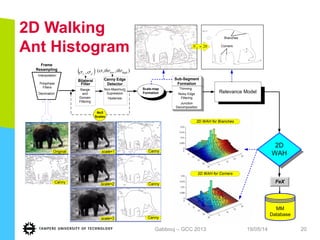
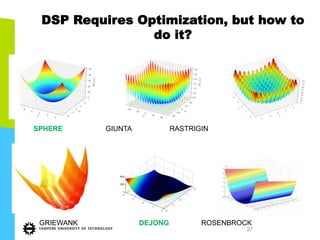
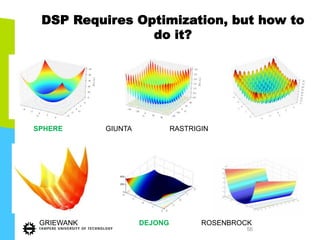
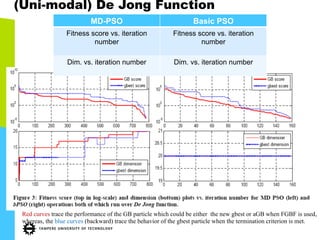
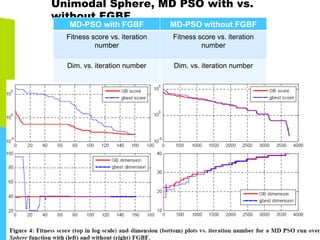
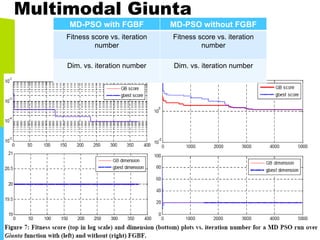
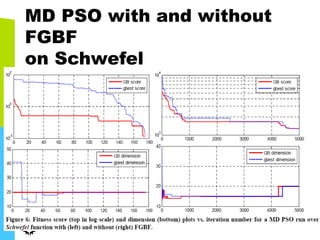
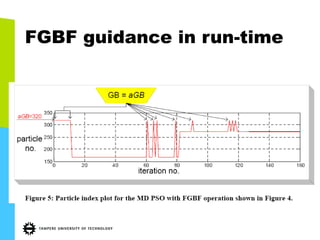
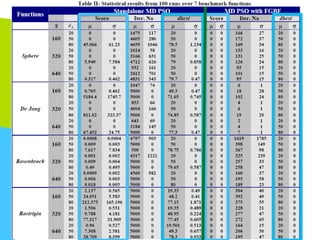
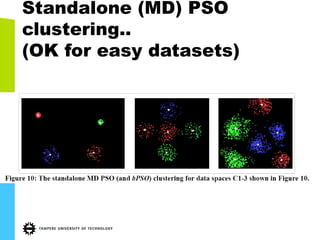
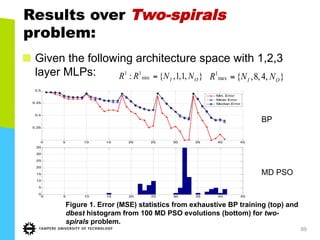
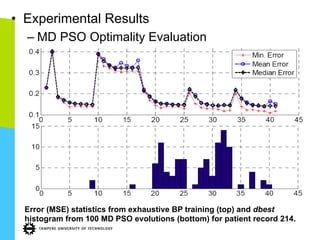
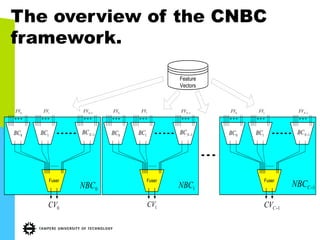
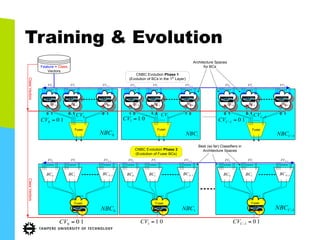
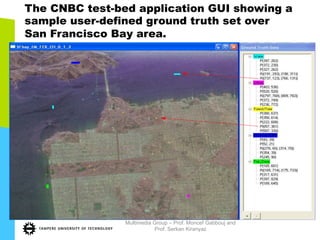
Machine Learning Tools and Particle Swarm Optimization for Content-Based Search in Big Multimedia Databases

Machine Learning Tools and
Particle Swarm Optimization for
Content-Based Search in Big
Multimedia Databases
Moncef Gabbouj
Academy of Finland Professor
Tampere University of Technology
Tampere, Finland

OUTLINE
v Big Data
v How to explore Big Data
v Prescriptive Analytics
v Future Trends and Policies
v Conclusions and Recommendations
19/05/14Gabbouj – GCC 2013 2

OUTLINE
v Big Data
v Conclusions and Recommendationsand
Recommendations
19/05/14Gabbouj – GCC 2013 3

Big Data Sources
19/05/14Gabbouj – GCC 2013 4
Source: King et. al., IEEE BD 2013

What is Big Data?
•  File/Object Size,
19/05/14Gabbouj – GCC 2013 5
Big Data refers to datasets which grow so large and
complex that it is no longer possible to capture, store,
manage, share, analyze and visualize within the current
computational architecture, display and storage capacity.
Source: King et. al., IEEE BD 2013

The 4V of Big Data
19/05/14Gabbouj – GCC 2013 6

Big Data in Science (1/2)
•  10 PB/year at start, 1000 PB in 10 years!
19/05/14Gabbouj – GCC 2013 7

Big Data in Science (2/2)
19/05/14Gabbouj – GCC 2013 8
Large Synoptic Survey Telescope (Chili)
~5-10 PB/year at start in 2012
~100 PB by 2025
Pan-STARRS (Hawaii)
– now: 800 TB/year
– soon: 4 PB/year

Big Data in Business Sectors
19/05/14Gabbouj – GCC 2013 9

Big Data Generated from Smart Grids
19/05/14Gabbouj – GCC 2013 10

19/05/14Gabbouj – GCC 2013 11

OUTLINE
v Big Data
v How to explore Big Data?
Recommendations
19/05/14Gabbouj – GCC 2013 12

How to Explore Big Data?
19/05/14Gabbouj – GCC 2013 13
Source: AYATA Media

OUTLINE
v Big Data
Recommendations
19/05/14Gabbouj – GCC 2013 14

Descriptive Analytics
§  Classic descriptors
§  Advanced representations and tools
§  Optimization: PSO
§  Evolutionary Neural Networks
§  Advanced Clustering: CNBC
§  Feature synthesis
§  Big tools for Big Data
19/05/14Gabbouj – GCC 2013 15

16
Content-Based Image Retrieval
Scenario

An Automatic Object Extraction Method
Based on Multi-scale Sub-segment
Analysis over Edge Field
19/05/14Gabbouj – GCC 2013 17
Original scale = 1 scale = 3scale = 2
Canny Edge Field
Segmentation
Scale-Map CL SegmentSub-Segments

Object Extraction Examples
19/05/14Gabbouj – GCC 2013 18
(a)
2=CLN
(g)
2=CLN
(d)
3=CLN
(e)
2=CLN
(c)
1=CLN
(b)
2=CLN
(h)
1=CLN
(f)
1=CLN

Quantum Mechanics Principles for
Automatic Object Extraction
19/05/14Gabbouj – GCC 2013 19

1
2

3
Goal: Apply principles of Quantum Mechanics through solving the time-
independent Schrödinger’s equation:
to extract objects through an innovative and multi-disciplinary research track.
Object segmentation examples with tunneling effect. Red arrows indicate the
regions where tunneling occurs

2D Walking
Ant Histogram
19/05/14Gabbouj – GCC 2013 20
Thinning
Noisy Edge
Filtering
Junction
Decomposition
Sub-Segment
Formation
Relevance Model
FeX
Bilateral
Filter
Range
and
Domain
Filtering
( )dr σσ ,,
Canny Edge
Detector
Non-Maximum
Supression
Hysterisis
Polyphase
Filters
Interpolation
Decimation
Frame
Resampling
NoS
Scales
Scale-map
Formation
),,( highlow thrthrσ
MM
Database
scale=1
scale=3
scale=2
Canny
Canny
CannyOriginal
Canny
2D
WAH
2D WAH for Branches
2D WAH for Corners
Corners
Branches
20=SN

2D WAH Corner Detection
Original Image
Proposed
Corner Detector
19/05/14Gabbouj – GCC 2013 21

2D WAH Image Retrieval
19/05/14Gabbouj – GCC 2013 22
Stamps
Stop SignTower
Pyramid

M-MUVIS
Retrieval on Nokia 9500
19/05/14Gabbouj – GCC 2013 23
Query Image
11 best matched
retrieved images

Lessons Learned (the hard way)
Clustering
helps!
Gabbouj – GCC 2013 24
Special type of classifiers
– media content
– Efficient (optimized)
– Scalable
– Dynamic (incremental)

Prescriptive Analytics
§  Classic signal and imge processing and
analysis tools
§  Improved Features: EFS
19/05/14Gabbouj – GCC 2013 25

Optimization..
•  Weak Definition: Search for a minimum or
maximum of a function, system or surface.
•  Deterministic Greedy Descent Methods
–  Function Minimization: Gradient Descent Methods
–  Feed-Forward ANN Training: Back-Propagation (BP)
–  GMM Training: Expectation-Maximization (EM)
–  Data Clustering: K-means (K-medians, FCM, etc.)
–  ...
•  They are very efficient for uni-modal functions or
surfaces, i.e. Fast, guaranteed convergence,
simple..
•  What about multi-modal functions or surfaces?

27

GRIEWANK DEJONG ROSENBROCK
SPHERE GIUNTA RASTRIGIN
DSP Requires Optimization, but how to
do it?

Greedy Descent Methods:
Problems..
•  They converge to the
nearest local optimum.
•  Random Initialization
à Random
Convergence..
•  Results are unreliable,
unrepeatable and sub-
optimum.
•  Only “works” for simple
problems..
•  Take e.g. K-means
clustering
•  K?

How does Nature Optimize?
•  We wish to design something – we want the best
possible (or, at least a very good) design.
•  The set S is the set of all possible designs. It is
always much too large to search through this set
one by one, however we want to find good
examples in S.
•  In nature, this problem seems to be solved
wonderfully well, again and again and again, by
evolution.
•  Nature has designed millions of extremely complex
machines, each almost ideal for their tasks using
the evolution as the only mechanism.

Swarm Intelligence
•  How do swarms of birds, fish, etc. manage to
move so well as a unit? How do ants manage to
find the best sources of food in their environment.
Answers to these questions have led to some very
powerful new optimisation methods, that are
different to EAs. These include Ant Colony
Optimisation (ACO), and Particle Swarm
Optimisation (PSO).
•  Also, only by studying how real swarms work are
we able to simulate realistic swarming behaviour

Evolutionary Computation
Algorithms
1. Initialize the population
2. Calculate the fitness of each individual in the
Population.
3. Reproduce selected individuals to form a new
generation, e.g. in GA: Perform evolutionary
operations such as crossover and mutation
4. Loop to step 2 until some condition is met
ü The Rule: The survival of the fittest..

Evolutionary Computation
Paradigms
•  Genetic algorithms (GAs) - John Holland
•  Evolutionary programming (EP) - Larry Fogel
•  Evolution strategies (ES) - I. Rechenberg
•  Genetic programming (GP) - John Koza
•  Particle swarm optimization (PSO) - Kennedy
& Eberhart (1995)

SWARMS
•  Coherence without
choreography
•  Particle swarms;
“.. behavior of a single
organism in a swarm is
often insignificant but
their collective and
social behavior is of
paramount importance”

Intelligent Swarm
•  A population of interacting individuals that
optimizes a function or goal by collectively adapting
to the local and/or global environment
•  Swarm intelligence ≅ collective adaptation
•  A “swarm” is an apparently disorganized collection
(population) of moving individuals that tend to
cluster together while each individual seems to be
moving in a random direction
•  We also use “swarm” to describe a certain family of
social processes

Introduction to Particle
Swarm Optimization (PSO)
A concept for optimizing nonlinear
functions
•  Has roots in artificial life and evolutionary
computation
•  Developed by Kennedy and Eberhart (1995)
•  Simple in concept
•  Easy to implement
•  Computationally efficient
•  Effective on a variety of problems

Features of Particle Swarm
Optimization
•  Population initialized by assigning random
positions and velocities; potential solutions are
then flown through hyperspace.
•  Each particle keeps track of its “best” (highest
fitness) position in hyperspace.
•  This is called pbest for an individual particle
•  It is called gbest for the best in the population
•  At each time step, each particle stochastically
accelerates toward its pbest and gbest (or
lbest).

Particle Swarm Optimization
Process
1. Initialize population in hyperspace.
2. Evaluate fitness of individual particles.
3. Modify velocities based on previous best and
global (or neighborhood) best.
4. Terminate on some condition.
5. Go to step 2.

19
/0
5/
14
39
Velocity Update Equation for a PSO
particle
•  Basic version:
where d is the dimension, c1 and c2 are positive
constants, rand and Rand are random functions,
and w is the inertia weight.
New v = (particle Inertia) + (Cognitive term) +
(Social term)

Shortcomings of PSO
•  The dimensionality of the solution space must
be fixed
•  Premature convergence to local minima
•  Degeneracy of the search space in case of
high dimensionality (particle velocities lapse into
degeneracy in such a way that successive range is
restricted in a sub-plane of the full search hyper-plane)
44

Extending PSO to Work on Varying
Dimensionality: MD PSO Algorithm
•  Instead of operating at a fixed dimensionality N,
the MD PSO algorithm is designed to seek both
positional and dimensional optima within a
dimensionality range, (Dmin<N<Dmax).
•  To do this, each particle is iterated through two
interleaved PSO processes:
–  a regular positional PSO, i.e. the traditional velocity
update and due positional shift in N dimensional
search (solution) space,
–  a dimensionality PSO, which allows the particle to
navigate through different dimensionalities.

MD PSO Algorithm (1)
•  Each particle keeps track of its last position,
velocity and personal best position (pbest) in a
particular dimension so that when it re-visits
that the same dimension at a later time, it can
perform its regular “positional” fly using this
information.
•  The dimensional PSO process of each particle
may then move the particle to another
dimension where it will remember its positional
status and keep “flying” within the positional
PSO process in this dimension, and so on.

MD PSO Algorithm (2)
•  The swarm keeps track of the gbest particles in
each dimensionality, indicating the best (global)
position so far achieved (and will be used in the
regular velocity update equation for that
dimensionality).
•  Similarly the dimensionality PSO process of each
particle uses its personal best dimensionality in
which the personal best fitness score has so far
been achieved.
•  Finally, the swarm keeps track of the global best
dimension, dbest, among all the personal best
dimensionalities.
•  The gbest particle in dbest dimensionality

MD PSO illustration..
Multimedia Group – Profs. Moncef Gabbouj
and Serkan Kiranyaz
Go to d
=23
gbest(3)
9
7
3)(9 =txd
gbest(2)d=2
d=3
2)(7 =txd
MD PSO
(dbest) a
23)( =txda
OK!

A Second Extension of PSO: Fractional
Global Best formation (FGBF)
•  Motivation: Both PSO and MD PSO may suffer
from premature convergence (i.e. convergence to a
local optimum)
•  Idea: Can we provide a better “guide”
than the Swarm’s Global Best?
•  Proposal: Introduce a new particle to the swarm
whose j’th component is the corresponding
swarm’s best component (i.e. component-wise best
particle). This new particle is called an artificial GB
particle (aGB) and the process is called Fractional
GB formation (FGBF).

FGBF (2)
X
1
3
8 +
gbest
x
y
bestxΔ
bestyΔ
),( 11 yx
),( 88 yx
),( 33 yx
),(: 83 yxaGB
0
),( TT yxTarget:
FGBF
FGBF

FGBF (3)
•  aGB can and usually is better than gbest, especially at the beginning of the
iteration
•  aGB has the advantage of assessing each dimension of every particle in
the swarm individually, and uses the most promising (or simply the best)
components among them.
•  Using the available diversity among individual dimensional components,
FGBF can prevent the swarm from being trapped in a local optimum due to
its ongoing and varying FGBF operations.
•  At each iteration, FGBF is performed after the assignment of the swarm’s
gbest particle and the best one between the two will be the GB particle,
which is used in the swarm’s velocity updates, i.e., the swarm will be
guided always by the best (winner) GB particle at any time.
•  What are the limitations of FGBF? (requires the component-wise
evaluation of the fitness function, i.e. it’s a problem-dependent)

Experimental Results
1- Function Minimization

56

GRIEWANK DEJONG ROSENBROCK
SPHERE GIUNTA RASTRIGIN
DSP Requires Optimization, but how to
do it?

(Uni-modal) De Jong Function
MD-PSO Basic PSO
Fitness score vs. iteration
number
number
Dim. vs. iteration number Dim. vs. iteration number
Red curves trace the performance of the GB particle which could be either the new gbest or aGB when FGBF is used,
whereas, the blue curves (backward) trace the behavior of the gbest particle when the termination criterion is met.

Unimodal Sphere, MD PSO with vs.
without FGBF
MD-PSO with FGBF MD-PSO without FGBF
number
number

Multimodal Giunta
MD-PSO with FGBF MD-PSO without FGBF
number
number

MD PSO with and without
FGBF
on Schwefel

Effects of dimension and
swarm size
GriewankRastring
S = 80 S = 320
d0 = 20, d0 = 80

65
2. Application to Data
Clustering
•  In clustering, similar to other PSO applications,
each particle represents a potential solution at
a particular time t, i.e. the particle a in the
swarm, is formed as,
•  where is the jth (potential) cluster centroid
in N dimensional data space and K is the
number of clusters fixed in advance.
},..,,..,{ 1 Sa xxx=ξ
jajaKajaaa ctxccctx ,,,,1, )(},..,,..,{)( =⇒=
jac ,

Application to Data
Clustering
•  Note that contrary to nonlinear function minimization in the
earlier section, the data space dimension, N, is now
different than the solution space dimension, K.
Furthermore, the fitness function, f that is to be optimized,
is formed with respect to two widely used criteria in
clustering:
•  Compactness: Data items in one cluster should be similar
or close to each other in N dimensional space and different
or far away from the others when belonging to different
clusters.
•  Separation: Clusters and their respective centroids should
be distinct and well-separated from each other.
∑ ∑= ∈
−=Δ
K
k cx
pkKmeans
kp
xc
1
2
∑
∑
=
∈∀
−
=
+−+=
K
j ja
xz
pja
ae
aeaaa
x
zx
K
xQwhere
xQwxdZwZxdwZxf
jap
1 ,
,
3minmax2max1
,1
)(
)())((),(),(

67
MD PSO & FGBF for
Data Clustering
•  Particle a in the swarm has the following form:
and represents a potential solution (i.e. the
cluster centroids) for number of clusters
where the jth component is the jth cluster
centroid.
ja
txd
jatxdajaa
txd
a ctxxccctxx a
a
a
,
)(
,)(,,1,
)(
)(},..,,..,{)( =⇒=
)(txda

Data Clustering in 2D:
Some Synthetic Examples

Standalone (MD) PSO
clustering..
(OK for easy datasets)

S. Kiranyaz, T. Ince, A. Yildirim and M. Gabbouj, “Fractional Particle Swarm
Optimization in Multi-Dimensional Search Space”, IEEE Transactions on
Systems, Man, and Cybernetics – Part B, pp. 298 – 319, vol. 40, No. 2, April
2010.
S. Kiranyaz, T. Ince, and M. Gabbouj, “Stochastic Approximation Driven
Particle Swarm Optimization with Simultaneous Perturbation (Who will
guide the guide?)”, Applied Soft Computing Journal, 11(2), pp. 2334-2347,
2011.

Dominant Color Extraction
based on Dynamic
Clustering by Multi-
Dimensional Particle Swarm
Optimization
Median-Cut
(Original)
MPEG-7
DCD
Proposed
Serkan Kiranyaz, Stefan Uhlmann, Turker Ince and
Moncef Gabbouj, "Perceptual Dominant Color
Extraction by Multi-Dimensional Particle Swarm
Optimization, “EURASIP Journal on Advances in
Signal Processing, vol. 2009 (2009), Article
451638, 13 pages, doi:10.1155/2009/451638

Experimental Results
•  We have made comparative evaluations against MPEG-7 DCD over a
sample database with 110 images, which are selected from Corel
database in such a way that the prominent colors (DCs) can be
selected by ground-truth:
0 20 40 60 80 100 120
0
5
10
15
20
25
image number
DC Number Ts=15, Ta=1%
Ts=25, Ta=1%
Ts=25, Ta=5%
Figure 4: Number of DC plot from three different MPEG-7 DCDs over the
sample database.
Note how the number of DCs is strictly dependent to the parameters used
and can vary significantly, e.g. between 2 to 25 even for a particular image.

Median-Cut
(Original)
MPEG-7
DCD
Proposed
Median-Cut
algorithm
produces 256
(maximum)
colors, which is
almost identical
to the original
image.

Median-Cut
(Original)
MPEG-7
DCD Proposed

•  S. Kiranyaz, S. Uhlmann, T. Ince, and M. Gabbouj,
“Perceptual Dominant Color Extraction by Multi-
Dimensional Particle Swarm Optimization”, EURASIP
Journal on Advances in Signal Processing, vol. 2009,
Article ID 451638, 13 pages, 2009. doi:
10.1155/2009/451638.
Median-Cut
(Original)
MPEG-7
DCD Proposed
Median-Cut
(Original)
MPEG-7
DCD
Proposed

OUTLINE
•  Optimization Tools (PSO and extensions)
•  Applications in function minimization, data
clustering and image retrieval
•  Machine Learning tools
– Evolving NNs with MD PSO
– Novel Classifiers (CNBC)
– Evolutionary feature synthesis
•  Applications in CBIR
•  Conclusions Multimedia Group – Prof. Moncef Gabbouj and
Prof. Serkan Kiranyaz

Unsupervised Design of Artificial Neural
Networks via Multi-Dimensional Particle
Swarm Optimization
S. Kiranyaz, T. Ince, A. Yildirim and M. Gabbouj, “Evolutionary Artificial Neural
Networks by Multi-Dimensional Particle Swarm Optimization”, Neural Networks,
vol. 22, pp. 1448 – 1462, Dec. 2009. (top 5th downloaded paper from Elsevier
Journal since 2009)

Artificial Neural Networks
(ANNs)
•  Neural Networks are computer programs designed to recognize patterns
and learn like the human brain.
•  Used for prediction and classification. Iteratively determine best weights.
(input/hidden/output layers)
•  After introduction of simplified neurons by McCulloch and Pitts in 1943,
ANNs have been applied widely to many application areas, most of which
used feed-forward ANNs , or the so-called multi-layer perceptrons (MLPs)
with Back Propagation (BP) training algorithm.
•  For training ANNs, many researchers reported that Evolutionary Algorithms
(EAs), such as genetic algorithm, evolutionary programming, and PSO, can
outperform BP specially for large networks. In addition, EAs are population
based stochastic processes and they can avoid being trapped in a local
optimum.
•  Evolutionary ANNs can be automatically designed (internal structure and
parameters) according to the problem.

Introduction
"   A novel technique for automatic design of Artificial Neural
Networks (ANNs) by evolving to the optimal network
configuration(s) within an architecture space.
•  With the proper encoding of the network configurations and
parameters into particles, MD PSO can then seek for
positional optimum in the error space and dimensional
optimum in the architecture space.
•  The efficiency and performance of the proposed technique
is demonstrated over one of the hardest synthetic
problems. The experimental results show that MD PSO
evolves to optimum or near-optimum networks in general.

MD PSO for evolving ANNs
•  MD PSO negates the need of fixing the
dimension of the solution space in advance.
We then adapt MD PSO technique for
designing (near-) optimal ANNs.
•  The focus is particularly drawn on automatic
design of the feed-forward ANNs and the
search is carried out over all possible
network configurations within the specified
architecture space.

Main Idea:
•  All potential network configurations are
transformed into a hash (dimension) table with a
proper hash function where indices represent the
solution space dimensions of the particles, MD
PSO can then seek both positional and
dimensional optima in an interleaved PSO
process.
•  The optimum dimension found naturally
corresponds to a distinct ANN architecture where
the network parameters (connections, weights
and biases) can be resolved from the positional
optimum reached on that dimension.

19/05/14 85
Architecture Space Definition
over MLPs:
•  Layers:
•  Neurons: for
à
•  MLPs:Let F be the activation function applied
over the weighted inputs plus a bias, as
follows:
•  The training MSE, is formulated as,
},{ maxmin LL
},{ maxmin
ll
NN maxmin LlL ≤≤
},,...,,{ 1
min
1
minmin
max
O
L
I NNNNR −
= },,...,,{ 1
max
1
maxmax
max
O
L
I NNNNR −
=
l
k
lp
j
j
l
jk
lp
k
lp
k
lp
k ywswheresFy θ+== −−
∑ 1,1,,,
)(
( )∑∑∈ =
−=
Tp
N
k
Op
k
p
k
O
O
yt
PN
MSE
1
2,
2
1

19/05/14 86
Dim. Configuration Dim. Configuration
1 9 x 2 22 9 x 5 x 2 x 2
2 9 x 1 x 2 23 9 x 6 x 2 x 2
3 9 x 2 x 2 24 9 x 7 x 2 x 2
4 9 x 3 x 2 25 9 x 8 x 2 x 2
5 9 x 4 x 2 26 9 x 1 x 3 x 2
6 9 x 5 x 2 27 9 x 2 x 3 x 2
7 9 x 6 x 2 28 9 x 3 x 3 x 2
8 9 x 7 x 2 29 9 x 4 x 3 x 2
9 9 x 8 x 2 30 9 x 5 x 3 x 2
10 9 x 1 x 1 x 2 31 9 x 6 x 3 x 2
11 9 x 2 x 1 x 2 32 9 x 7 x 3 x 2
12 9 x 3 x 1 x 2 33 9 x 8 x 3 x 2
13 9 x 4 x 1 x 2 34 9 x 1 x 4 x 2
14 9 x 5 x 1 x 2 35 9 x 2 x 4 x 2
15 9 x 6 x 1 x 2 36 9 x 3 x 4 x 2
16 9 x 7 x 1 x 2 37 9 x 4 x 4 x 2
17 9 x 8 x 1 x 2 38 9 x 5 x 4 x 2
18 9 x 1 x 2 x 2 39 9 x 6 x 4 x 2
19 9 x 2 x 2 x 2 40 9 x 7 x 4 x 2
20 9 x 3 x 2 x 2 41 9 x 8 x 4 x 2
21 9 x 4 x 2 x 2

19/05/14 87
MD PSO for Evolving MLPs
•  At a time t, suppose that the particle a in the swarm,
has the positional component formed as,
•  Where and represent the sets of weights and
biases of the layer l. Note that the input layer (l=0) contains only
weights whereas the output layer (l=O) has only biases. By
means of such a direct encoding scheme, the particle a
represents all potential network parameters of the MLP
architecture at the dimension (hash index)
},..,,..,{ 1 Sa xxx=ξ
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
= −−
}{},{},{,...,
}{},{},{},{},{
)( 11
22110
)(
O
k
O
k
O
jk
kjkkjkjktxd
a
w
www
txx a
θθ
θθ
}{ l
jkw }{ l
kθ

The Two-spiral Problem
Many attempts, e.g.
Jia and Chua, IEEE International
Conference on Neural Networks,
1995.
The authors studied the effect of
input data representation on the
performance of back-propagation
neural network in solving a highly
nonlinear two-spiral problem.
Gabbouj - 2014

89
Results over Two-spirals
problem:
"   Given the following architecture space with 1,2,3
layer MLPs: },1,1,{: min
11
OI NNRR = },4,8,{max
1
OI NNR =
0 5 10 15 20 25 30 35 40 45
0.35
0.4
0.45
0.5
Min. Error
Mean Error
Median Error
0 5 10 15 20 25 30 35 40 45
0
5
10
15
20
25
30
35
Figure 1. Error (MSE) statistics from exhaustive BP training (top) and
dbest histogram from 100 MD PSO evolutions (bottom) for two-
spirals problem.
BP
MD PSO

Automated Patient-
specific Classification
of ECG Data
T. Ince, S. Kiranyaz, and M. Gabbouj, “A Generic and Robust System for Automated
Patient-specific Classification of Electrocardiogram Signals”, IEEE Transactions on
Biomedical Engineering, vol. 56, issue 5, pp. 1415-1426, May 2009.

91
System Overview
Dimension
Reduction
(PCA)
Expert
Labeling
Beat
Detection
Data Acquisition
Morph.
Feature
Extraction
(TI-DWT)
Patient-specific data:
first 5 min. beats
MD PSO:
Evolution + Training
Common data: 200 beats
Training Labels per beat
BeatClassType
Patient X
Temporal Features
ANN
Space

•  Experimental Results
– MD PSO Optimality Evaluation
Figure: Error (MSE) statistics from exhaustive BP training (top) and
dbest histogram from 100 MD PSO evolutions (bottom) for patient
record 222.

•  Experimental Results
– MD PSO Optimality Evaluation
Error (MSE) statistics from exhaustive BP training (top) and dbest
histogram from 100 MD PSO evolutions (bottom) for patient record 214.

19/05/14 94
Performance
Evaluation
% Normal PVC Other
Method Acc Sen Pp Sen Pp Sen Pp
DWT /
ANN (Inan et al.) 95.2 98.1 97 85.2 92.4 87.4 94.5
(DWT+PCA) /
MD PSO - ENN (Proposed) 97.0 99.4 98.9 93.4 93.3 87.5 97.8
For PVC detection, the following beat types are considered: Normal, PVC,
LBBB, RBBB, aberrated atrial premature, atrial premature contraction,
and supraventricular premature beats.

A “Divide & Conquer” Classifier Topology:
Collective Network of (Evolutionary) Binary
Classifiers

For CBIR, the key questions..
1) How to select certain features so as to achieve
highest discrimination over certain classes?
2) How to combine them in the most effective way?
3) Which distance metric to apply?
4) How to find the optimal classifier configuration for
the classification problem in hand?
5) How to scale/adapt the classifier if large number
of classes/features are incrementally introduced?
6) How to train the classifier efficiently to maximize
the classification accuracy?

Objectives:
•  Evolutionary Search: Seeking for the optimum network
architecture among a collection of configurations (the so-called
Architecture Space, AS).
•  Feature/Class Scalability: Support for varying number of
features and classes. A new feature/class can be dynamically
integrated into the framework without requiring a full-scale
initialization and re-evolution.
•  High efficiency for the evolution (or training) process: Using as
compact and simple classifiers as possible in the AS.
•  Online (incremental) Evolution: Continuous online/incremental
training (or evolution) sessions can be performed to improve the
classification accuracy.
•  Parallel processing: Classifiers can be evolved using several
processors working in parallel.

The CNBC framework..
•  Each NBC corresponds to a unique semantic class and
shall contain indefinite number of evolutionary binary
classifiers (BCs) in the input layer where each BC performs
binary classification over an individual feature.
•  Each BC in an NBC shall in time learn the significance of
individual dimensions of the corresponding feature vector
for the discrimination of its class.
•  Finally, a “fuser” BC in the output layer shall fuse the binary
outputs of all BCs in the input layer and outputs a single
binary output, indicating the relevance of each media item
to its class.

The overview of the CNBC
framework.
Feature
Vectors
0CV
1−NBC0BC 1BC
0FV 1FV 1−NFV
0NBC
Fuser
1−CCV
1−NBC0BC 1BC
0FV 1FV 1−NFV
1−CNBCFuser
1CV
1−NBC0BC 1BC
0FV 1FV 1−NFV
1NBC
Fuser

Class/Feature Scalability
•  The proposed CNBC framework makes the system
scalable to any number of classes since whenever
a new semantic class becomes available (user
defined), the system simply creates and trains a
new NBC for this class and thus the overall system
dynamically adapts to user demands of semantic
classes
•  CNBC is also scalable wrt features, i.e., whenever
a new feature is extracted, a new BC will be
created, trained and inserted into each NBC of the
system using the available Relevance Feedback,
while keeping the other BCs unchanged.

Training & Evolution
•  We shall be applying a “long term” learning strategy
where the previous RF logs shall be stored and used for
continuous, offline (“idle-time”) training of the entire
system, in order to improve the overall classification
performance.
•  The evolution will be applied over an architecture space –
not training of a single configuration. The architecture
space containing the best possible BCs (with respect to a
given criteria) shall always be kept intact and with each
ongoing RF session, each BC configuration will therefore,
“evolve” through a better state, whilst the best among all
at a given time shall be used for classification and
retrieval.

Training & Evolution
Feature + Class
Vectors
ClassVectors
1−NBC0BC 1BC
0FV 1FV 1−NFV
0NBC
1−NBC0BC 1BC
0FV 1FV 1−NFV
1NBC
1−NBC0BC 1BC
0FV 1FV 1−NFV
1−CNBC
Architecture Spaces
for BCs
0 1 0 1 0 1 0 1 0 1 0 11 0 1 0 1 0
0CV
Fuser
1CV
Fuser
1−CCV
Fuser
100 =CV 011 =CV 101 =−CCV
CNBC Evolution Phase 1
(Evolution of BCs in the 1st
Layer)
CNBC Evolution Phase 2
(Evolution of Fuser BCs)
1−NBC0BC 1BC
0FV 1FV 1−NFV
0NBC
1−NBC0BC 1BC
0FV 1FV 1−NFV
1−CNBC
1−NBC0BC 1BC
0FV 1FV 1−NFV
1NBC
100 =CV
Fuser
011 =CV
Fuser
101 =−CCV
Fuser
Best (so far) Classifiers in
Architecture Spaces
ClassVectors

CNBC for Polarimetric SAR
Image Classification
S. Kiranyaz, T. Ince, S. Uhlmann, and M. Gabbouj, “Collective Network of Binary
Classifier Framework for Polarimetric SAR Image Classification: An Evolutionary
Approach”, IEEE Transactions on Systems, Man, and Cybernetics – Part B, (in
Press).

The CNBC test-bed application GUI showing a
sample user-defined ground truth set over
San Francisco Bay area.
Multimedia Group – Prof. Moncef Gabbouj and

CET-1
CET-2 CET-3
Water Urban Forest FlatZones Mountain/Rock
Multimedia Group – Prof. Moncef Gabbouj and Prof. Serkan
Kiranyaz

Retrieval Results: With and
Without CNBC
4x2 sample queries in Corel_10 (qA and qB), and Corel_Caltech_30 (qC and qD)
databases Top-left is the query image.
Traditional With CNBCqA
Traditional With CNBCqB
Traditional With CNBCqC
Traditional With CNBCqD

Without CNBC
Traditional With CNBCqC

Without CNBC
Traditional With CNBCqD

Evolutionary Feature
Synthesis
Multimedia Group – Prof. Moncef Gabbouj
EFS
class-1
class-2
class-3

Evolutionary Feature Synthesis
Why do we Need it?
•  Discriminative features are essential
for classification, retrieval etc.
•  Semantic gap
–  Low level features cannot fully match
with the human perception of similarity
–  Higher level of understanding is
necessary
•  Using the experience/knowledge of
human similarity perception, highly
discriminative features can be
synthesized from low-level features.
Multimedia Group – Prof. Moncef Gabbouj

by MD PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-1
-0.5
0
0.5
1
(1,0)
1x
2x { }21
2
2
2
1 2,, xxxx
2D à 3D
(1,0)
2y
1y
class-1
class-2
)2sin( fxπ
1D à 1D
0 1
(FS-1)
class-1
class-2
(FS-2)
FV
Image
Database
FeX
MD-PSO based
Feature Synth. Fitness
Eval.
(1-AP)
Synt.
FV (1)Ground Truth
MD-PSO based
Feature Synth.
Synt.
FV (R)
Synt.
FV (R-1)

0x
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
Β
Β
Β
Α
=
K
K
d
jaxx
θ
θ
θ
...
...
2
2
1
1
1
,
where,
[ ] [ ) [ ] [ ]KiFNdj ii ,1,,1,,0,,1,0 1 ∈∈ℜ∈ΒΑ−∈ θ
⎣ ⎦ [ ] ⎣ ⎦ [ ]
)(
1,0,1
1,0,1,01
111
1
ii
iii
i
Operator
wwiwandw
NBiN
θ
βα
βα
βαβα
≡Θ
<≤−Β=−Α=
−∈=−∈Α=
Let:
1x
1αx
1βx
2βx
Kxβ
1−Nx
1αw
1βw
2βw
Kwβ
1Θ 2Θ KΘ
0y
1y
jy
1−dy
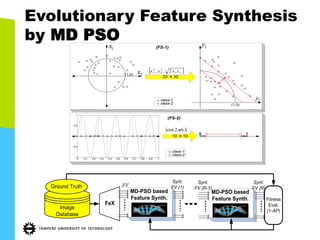
Original FV
(N-dimensional)
Synthesized FV
(d-dimensional)

Overview of the Evolutionary
Feature Synthesizer
§  We perform an evolutionary search technique, which for each new
feature:
•  selects K+1 original (or synthesized ) features, f0,…, fK
•  scales the selected features using proper weights, w0,…, wK
•  selects K operators, Θ1,…, ΘK, to be performed over the (selected
and scaled) features
•  bounds the results using a non-linear operator (i.e. tangent
hyperbolic, tanh).
§  If the application of a specific operator, Θi, on features, fa and fb, is
denoted as Θi (fa, fb ) the synthesis formula used to form each new
feature may be given as follows:
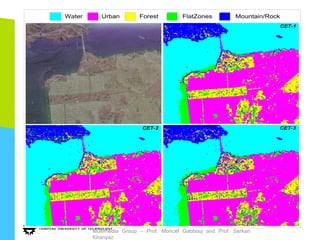
Multimedia Group – Prof. Moncef Gabbouj and Prof. Serkan Kiranyaz
( )( )( )( )( )1 2 1 0 0 1 1 2 2tanh ... , , ,... ,j K K K Ky w f w f w f w f−= Θ Θ Θ Θ

Some Fitness Functions
Ø It is practically not possible to use any direct retrieval
measure (e.g. ANMRR)
Ø We originally used clustering validity index (CVI)
combined with the number of false positives
Ø The retrieval results were not always improving even
though the fitness measure was greatly improved
Ø We adopted an approach similar to ANNs, but instead of
1-of-c coding we used output codes inspired by ECOC
Ø The fitness measure is the MSE to the target output
vector (divided by the output dimensionality)
( ) ( ) ( ) ( )mean, min,/ ,j j j j j i j i jf Z FP Z d c d c c= +

Experimental Results -
Setup
§  1000 image Corel database with 10 distinct classes
§  Low-level features used : RGB histogram, YUV histogram, LBP, Gabor
features

EFS RETRIEVAL
RESULTS
RGB color histogram
(4x4x4)Original Features EFS Run-2 & 3EFS Run-1

Multimedia Group – Prof. S. Kiranyaz

Conclusions
Ø  MD PSO is a poweful optimization tool which can be used
in several fields, including function minimization, clustering
and CBIR
Ø  CNBC represents the core clustering mechanism used in
MUVIS CBIR search engine
Ø  EFS framework presents a promising performance
Ø  MUVIS (with MD PSO, CNBC and EFS) is a step forward
towards accomplishing the Descriptive Analytics in ”BIG”
data

Particle Swarm Optimation
19/05/14Gabbouj – GCC 2013 120
Go to d
=23
gbest(3)
9
7
3)(9 =txd
gbest(2)d=2
d=3
2)(7 =txd
MD PSO
(dbest) a
23)( =txda
OK!
Multi-Dimensional PSO is a recent
optimization algorithm based on particle
swarms which finds the optimal
solution at the optimal dimension (it
can be applied to optimization in multi-
dimensional spaces where the dimension
of the solution space is not known a
priori).
S. Kiranyaz, T. Ince, A. Yildirim and M. Gabbouj,
“Fractional Particle Swarm Optimization in Multi-
Dimensional Search Space”, IEEE Trans. on
Systems, Man, and Cybernetics – Part B, pp. 298
– 319, vol. 40, No. 2, April 2010.

Evolutionary Artificial Neural Networks
Goal: Design optimal neural networks through an evolutionary
optimization process based on MD-PSO.
S. Kiranyaz, T. Ince, A. Yildirim and M. Gabbouj, “Evolutionary Artificial Neural Networks by Multi-
Dimensional Particle Swarm Optimization”, Neural Networks, vol. 22, pp. 1448 – 1462, Dec.
2009. 8th “most-cited” paper in the Journal of Neural Networks since 2008.
19/05/14Gabbouj – GCC 2013 121
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
= −−
}{},{},{,...,
}{},{},{},{},{
)( 11
22110
)(
O
k
O
k
O
jk
kjkkjkjktxd
a
w
www
txx a
θθ
θθ

Divide And Conquer
Collective Network of Binary Classifier (CNBC)
Framework
19/05/14Gabbouj – GCC 2013 122
Feature
Vectors
0CV
1−NBC0BC 1BC
0FV 1FV 1−NFV
0NBC
Fuser
1−CCV
1−NBC0BC 1BC
0FV 1FV 1−NFV
1−CNBCFuser
1CV
1−NBC0BC 1BC
0FV 1FV 1−NFV
1NBC
Fuser
Goal: Design an efficient classifier for multimedia databases which is highly scalable and its
kernel is continuously updated with the aid of the evolutionary MD-PSO technique.
S. Kiranyaz, T. Ince, S. Uhlmann, and M. Gabbouj, “Collective Network of Binary Classifier Framework for Polarimetric
SAR Image Classification: An Evolutionary Approach”, IEEE Trans. on Systems, Man, and Cybernetics – Part B, pp.
1169-1186, August 2012.

Retrieval Examples
19/05/14Gabbouj – GCC 2013 123

How to Explore Big Data?
19/05/14Gabbouj – GCC 2013 124
Source: AYATA Media

19/05/14Gabbouj – GCC 2013 125
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-1
-0.5
0
0.5
1
(1,0)
1x
2x { }21
2
2
2
1 2,, xxxx
2D à 3D
(1,0)
2y
1y
class-1
class-2
)2sin( fxπ
1D à 1D
0 1
(FS-1)
class-1
class-2
(FS-2)EFS
class-1
class-2
class-3
FV
Image
Database
FeX
MD-PSO based
Feature Synth. Fitness
Eval.
(1-AP)
Synt.
FV (1)Ground Truth
MD-PSO based
Feature Synth.
Synt.
FV (R)
Synt.
FV (R-1)

EFS Retrieval Results
19/05/14Gabbouj – GCC 2013 126
Original Features EFS Run-2 & 3EFS Run-1

Patient Specific EEG Segmentation
and Classification
19/05/14Gabbouj – GCC 2013 127
Data Acquisition
Patient
X
Feature
Extraction
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
Normalized
Feature

Vectors
Norm.
EEG
CNBC
EEG
Classification
Expert
Labels
Expert
Labeling
Early
EEG
Records

Patient Specific ECG Segmentation
and Classification
19/05/14Gabbouj – GCC 2013 128
Dimension
Reduction
(PCA)
Expert
Labeling
Beat
Detection
Data Acquisition
Morph.
Feature
Extraction
(TI-DWT)
Patient-specific data:
first 5 min. beats
MD PSO:
Common data: 200 beats
Training Labels per beat
BeatClassType
Patient X
Temporal Features
ANN
Space

Prescriptive Analytics
§  Classic signal and imge processing and
analysis tools
§  Improved Features: EFS
19/05/14Gabbouj – GCC 2013 129

Cloud CNBC
for Big Data
19/05/14Gabbouj – GCC 2013 130
Self-‐Organized
Binary
EFS
Cloud
c
NDEFS )5(),5(
Synthesized
Feature

Vectors
FV-‐1
FV-‐N
MM
Database
Feature
Vectors
FV-‐2
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
NBC
Cloud
(class
C-‐1)
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
Class
Vectors
1
)1(),1(
−C
NDNBC
1
)3(),3(
−C
NDNBC
1−CCV
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
NBC
Cloud
(class
0)
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
0CV
1−NBC
0BC
1BC
0NBC
1CV
1−NBC
0BC
1BC
1NBC
17CV
1−NBC
0BC
1BC
17NBC
class-‐0

Master
Fuser
BC
Class
Vectors
0CV
0
)1(),1( NDNBC
0
)3(),3( NDNBC
c
NDEFS )0(),0(
c
NDEFS )1(),1(
c
NDEFS )1(),1(
c
NDEFS )0(),0(
class
C-‐1

Master
Fuser
BC

19/05/14Gabbouj – GCC 2013 137

OUTLINE
v Big Data
Recommendations
19/05/14Gabbouj – GCC 2013 138

Future Trends
19/05/14Gabbouj – GCC 2013 139

IP Traffic Growth
19/05/14Gabbouj – GCC 2013 140

19/05/14Gabbouj – GCC 2013 141

EU Big Data Policies
The European Data Forum 2013 of EC projects
• BIG: Build a self-sustainable Industrial community around Big Data in Europe
• LOD2: Linked open data Web
• PlanetData: Large‐scale open-data sets management
• Optique: Efficient Big Data access
• Envision: Environmental services
• TELEIOS: Earth observation Big Data
• EUCLID: Professional training for Big Data practitioners
19/05/14Gabbouj – GCC 2013 142

Cloud Computing and Cloud
Enterprise
19/05/14Gabbouj – GCC 2013 143

OUTLINE
v Big Data
v Conclusions and Recommendations
19/05/14Gabbouj – GCC 2013 144

Conclusions and
Recommendations
o  Big Data is everywhere
o  Requires Big Tools and
proper training
o  Engineering education
landscape is changing
o  Big Data will transform
our lives - A new
generation
19/05/14Gabbouj – GCC 2013 145

Will Big Data change our lives?
19/05/14 147
Ä
Ö
Å

Machine Learning Tools and Particle Swarm Optimization for Content-Based Search in Big Multimedia Databases

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Machine Learning Tools and Particle Swarm Optimization for Content-Based Search in Big Multimedia Databases

Similar to Machine Learning Tools and Particle Swarm Optimization for Content-Based Search in Big Multimedia Databases (20)

More from Distinguished Lecturer Series - Leon The Mathematician

More from Distinguished Lecturer Series - Leon The Mathematician (20)

Recently uploaded

Recently uploaded (20)

Machine Learning Tools and Particle Swarm Optimization for Content-Based Search in Big Multimedia Databases