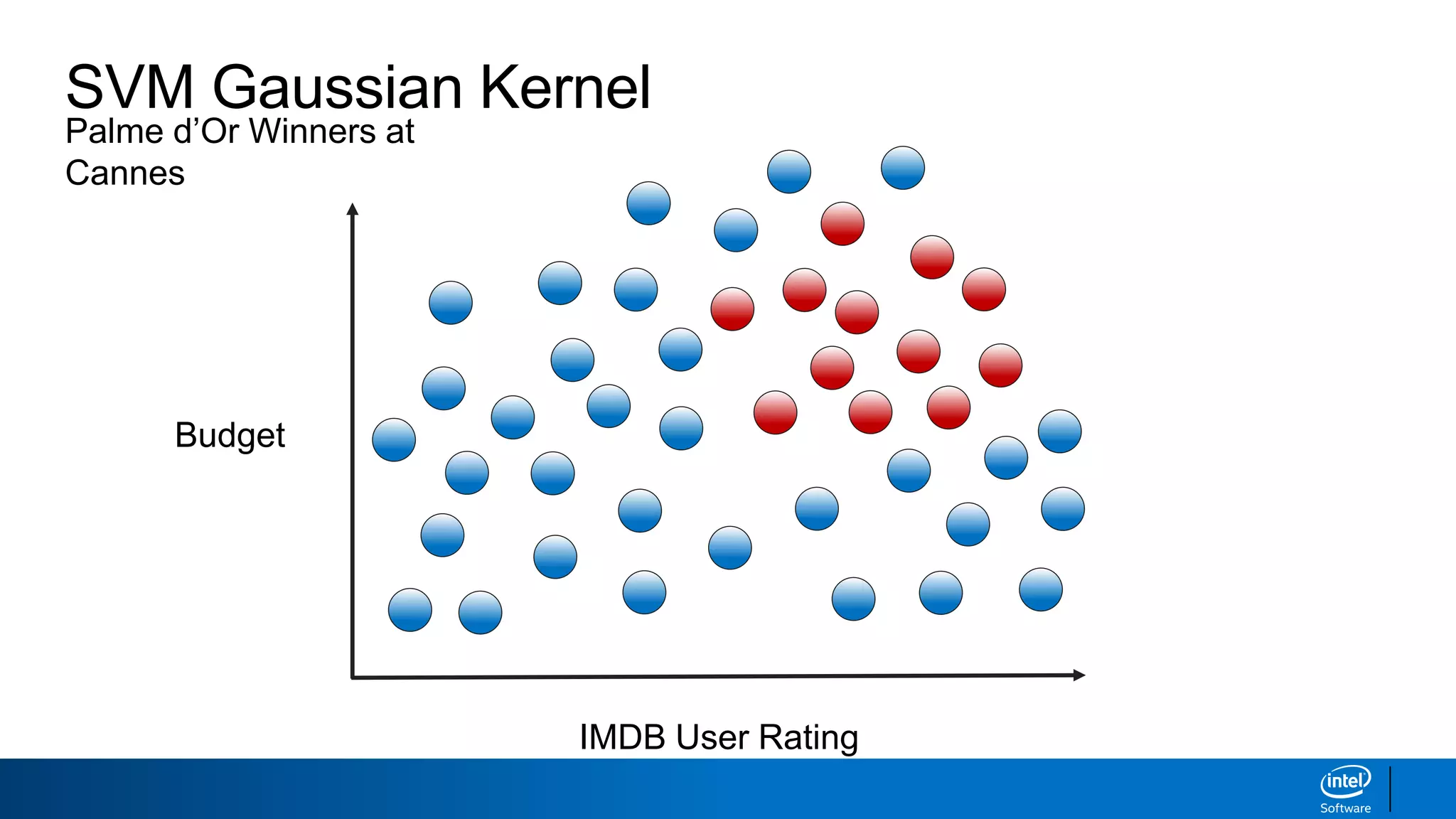
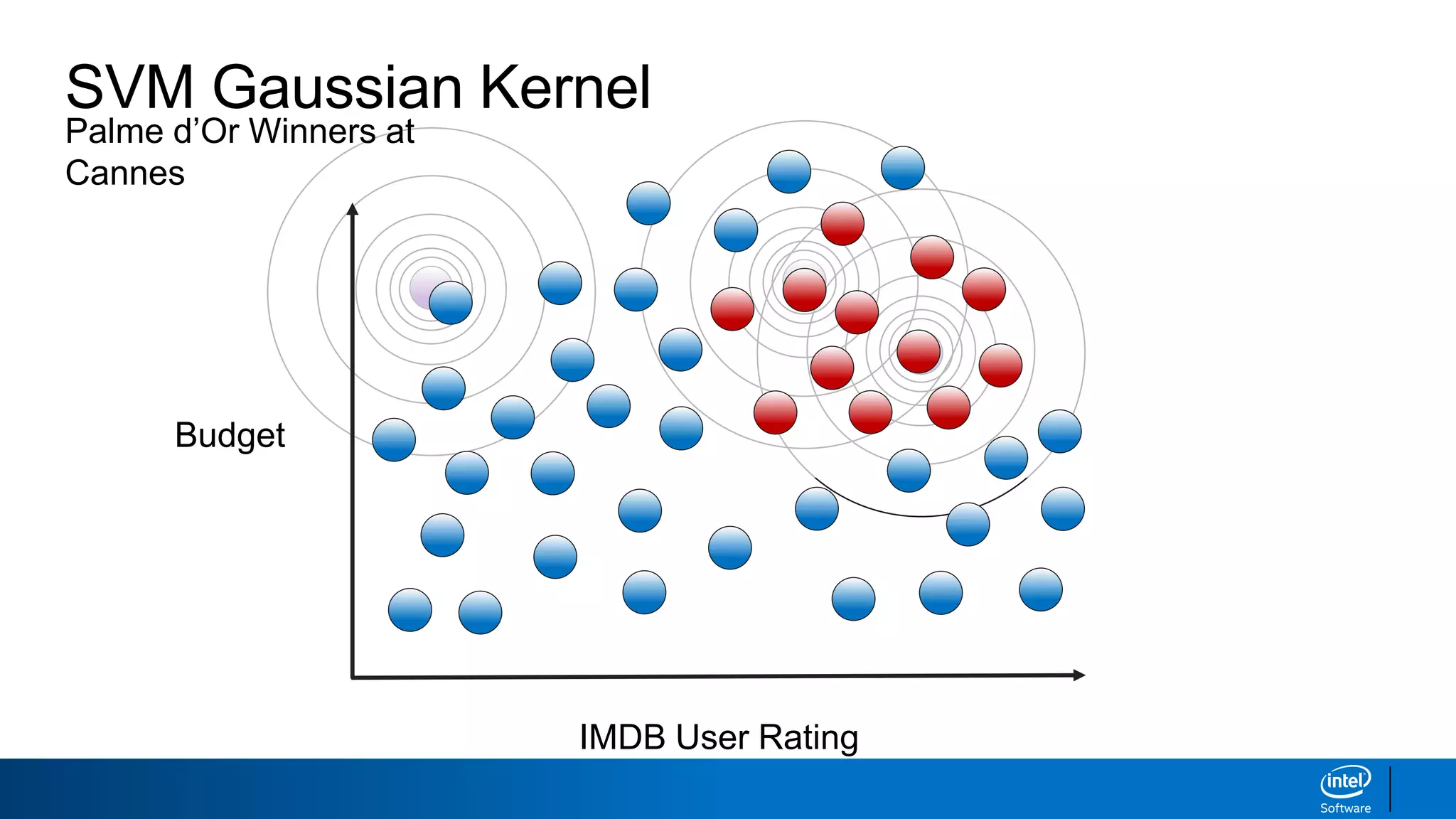
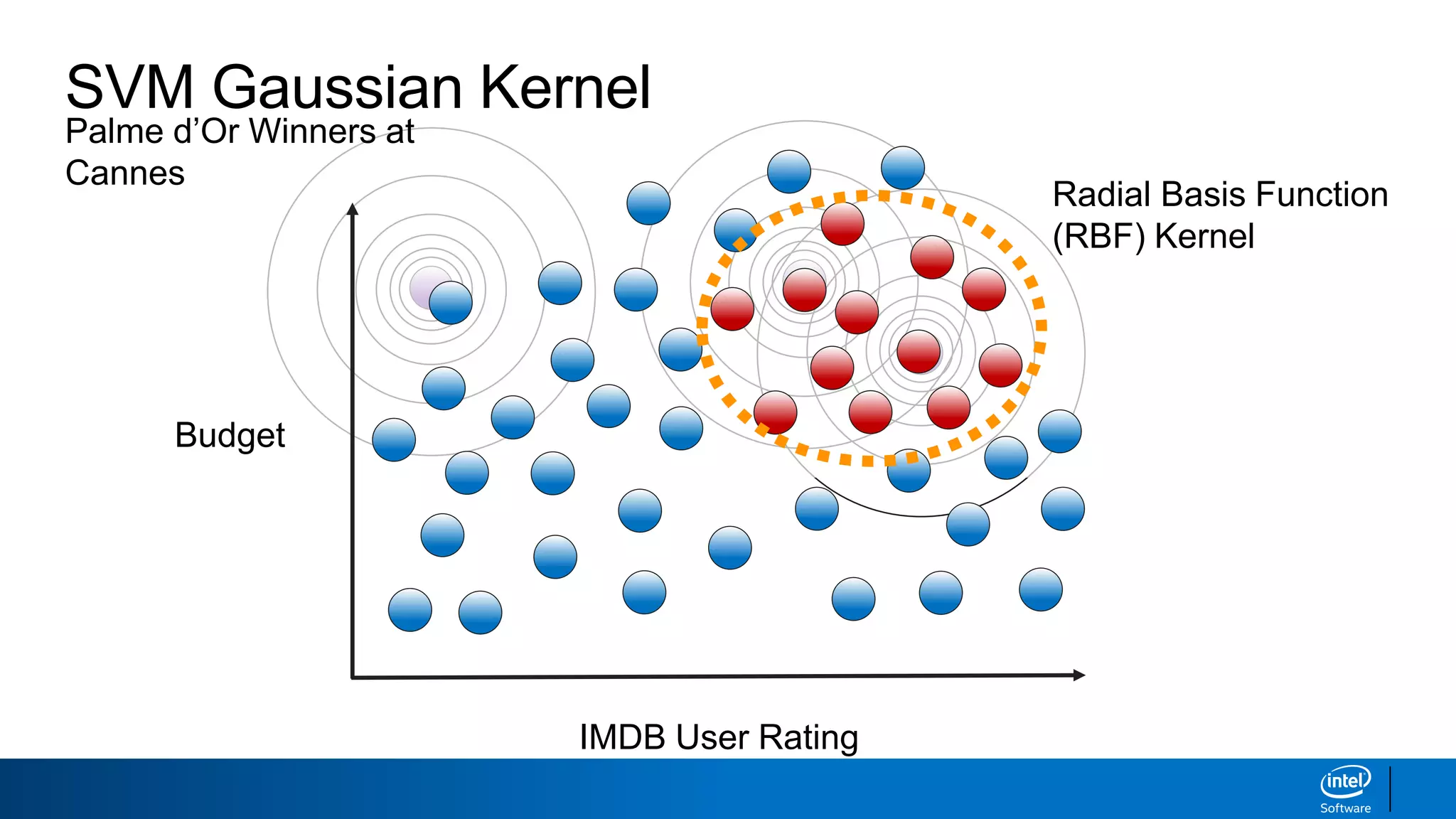
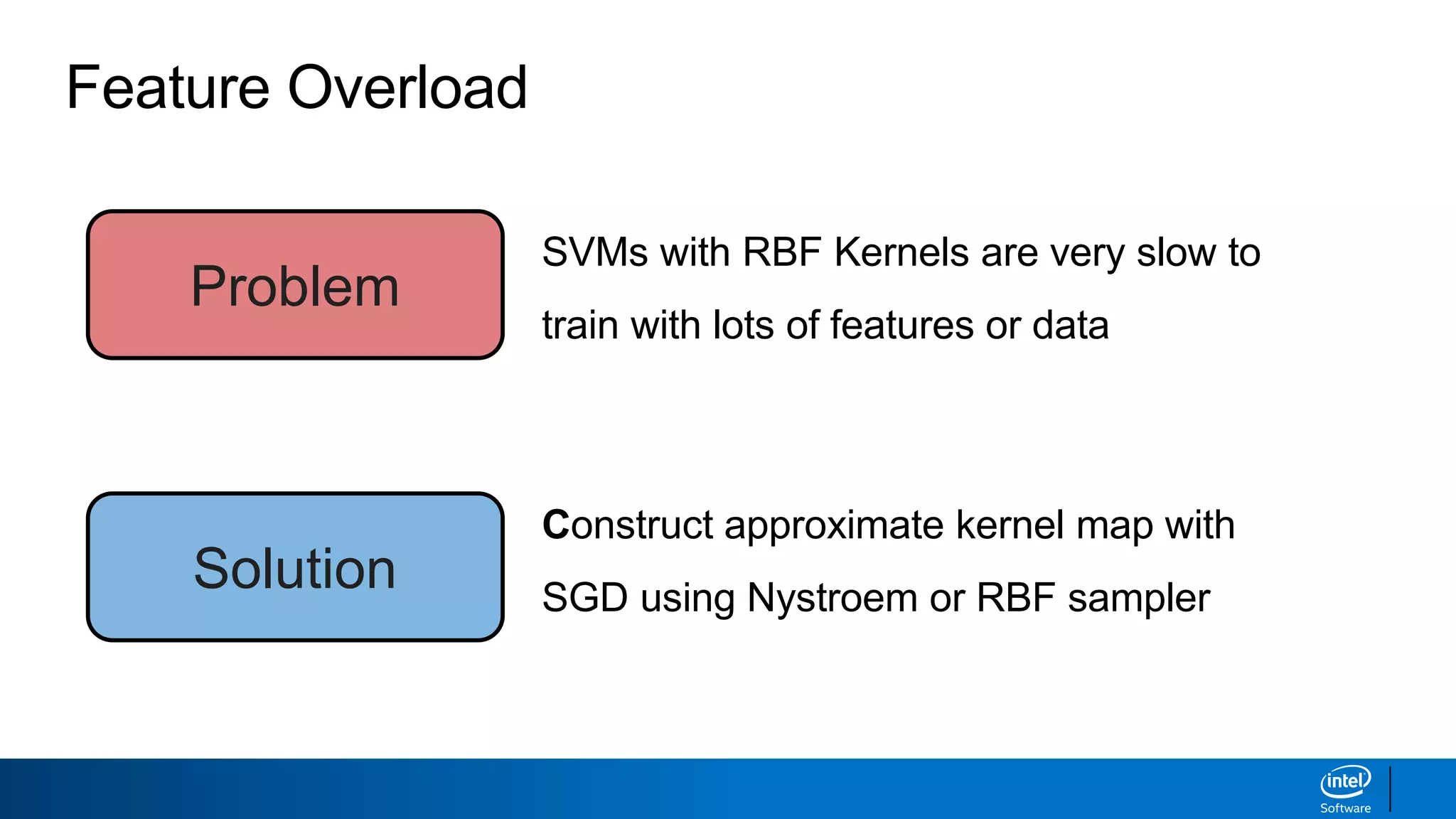
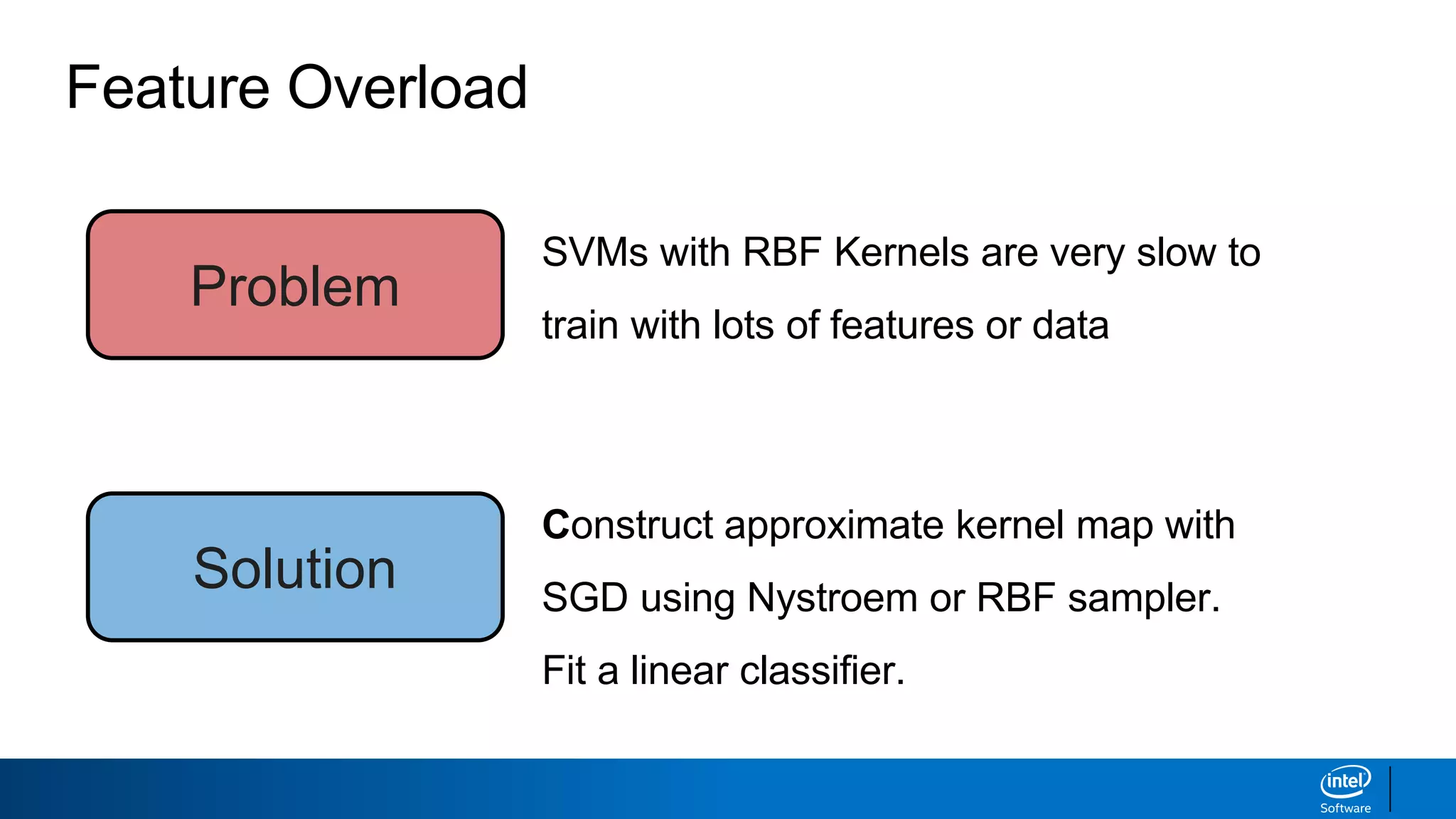
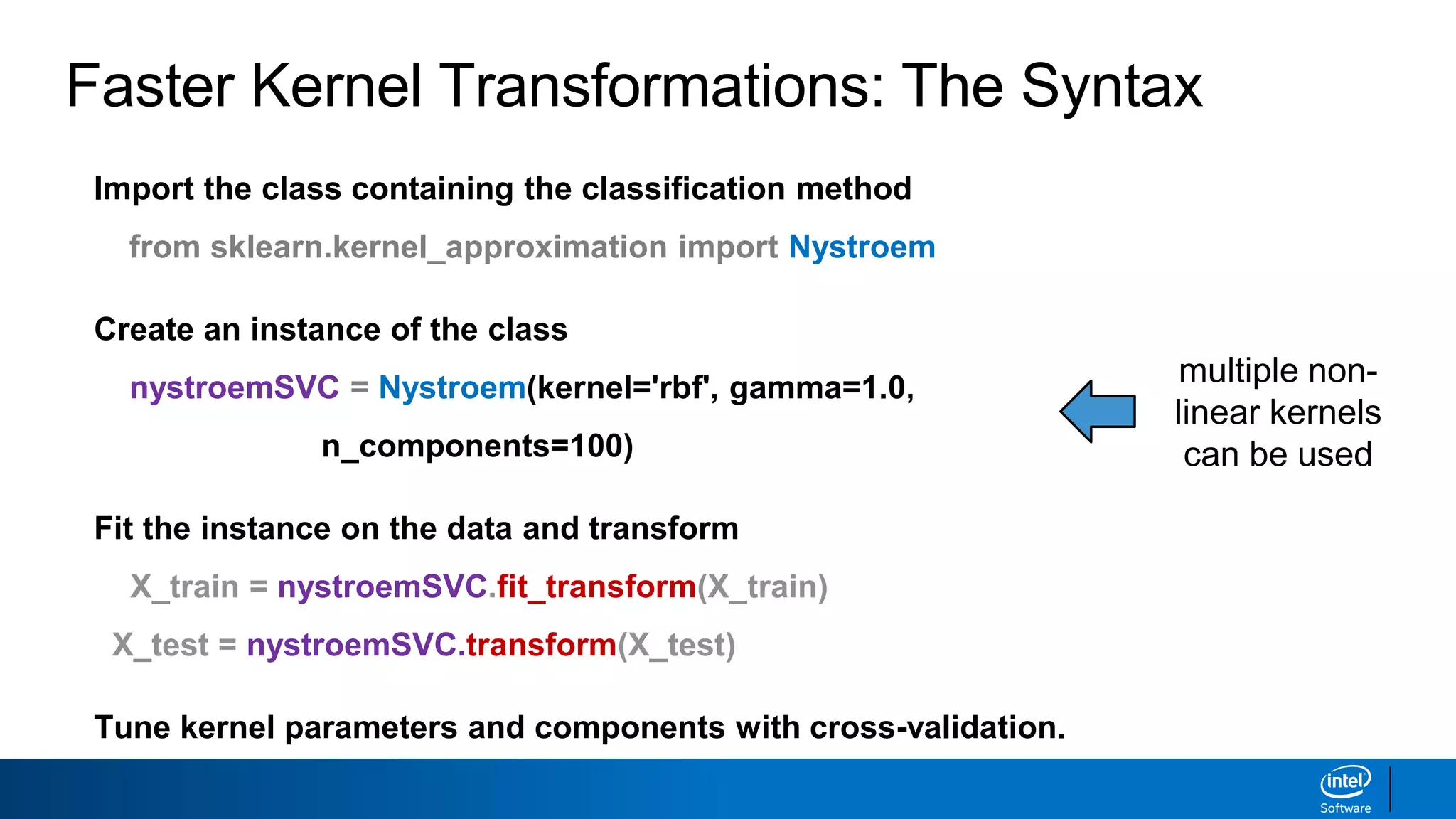
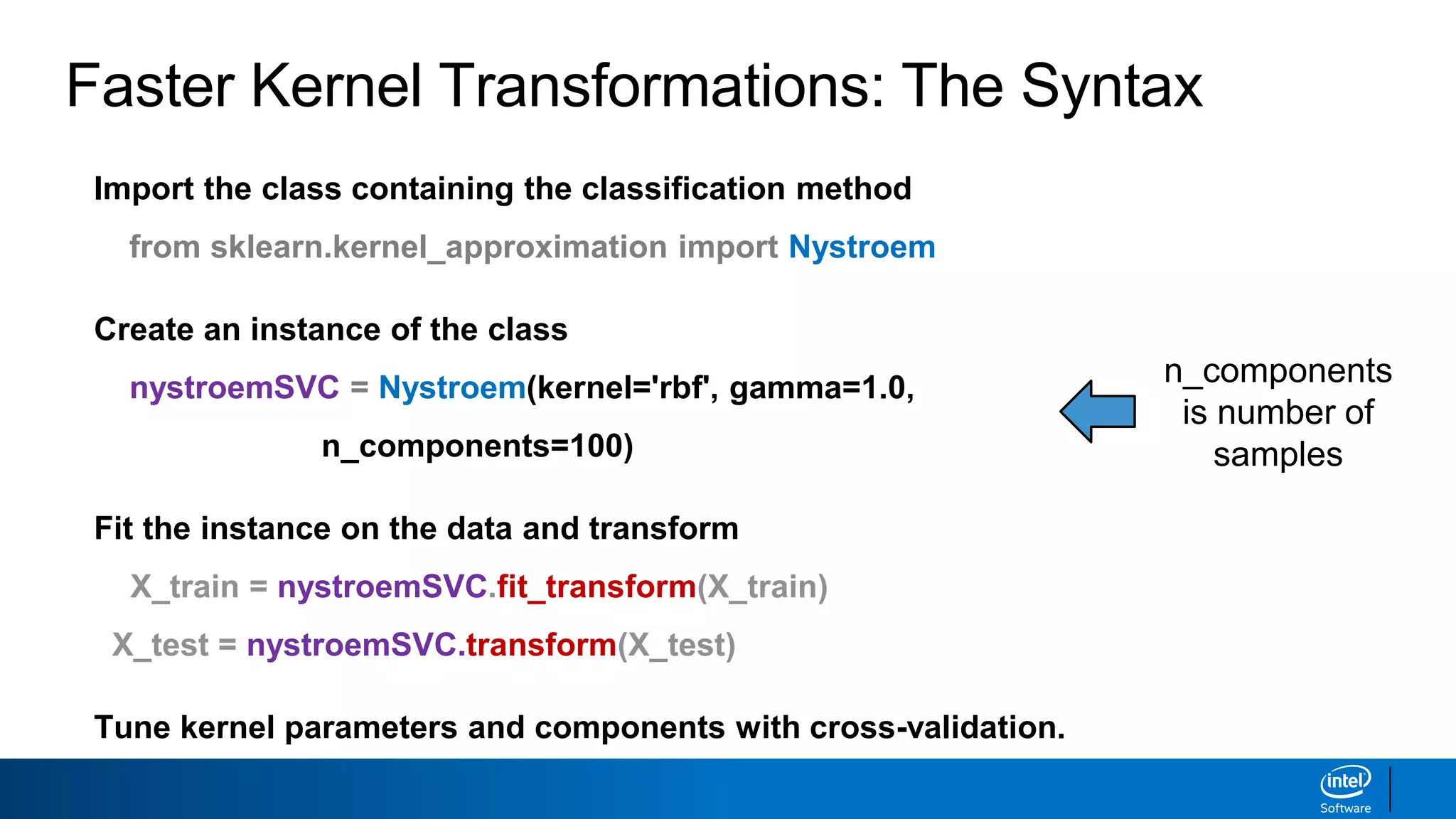
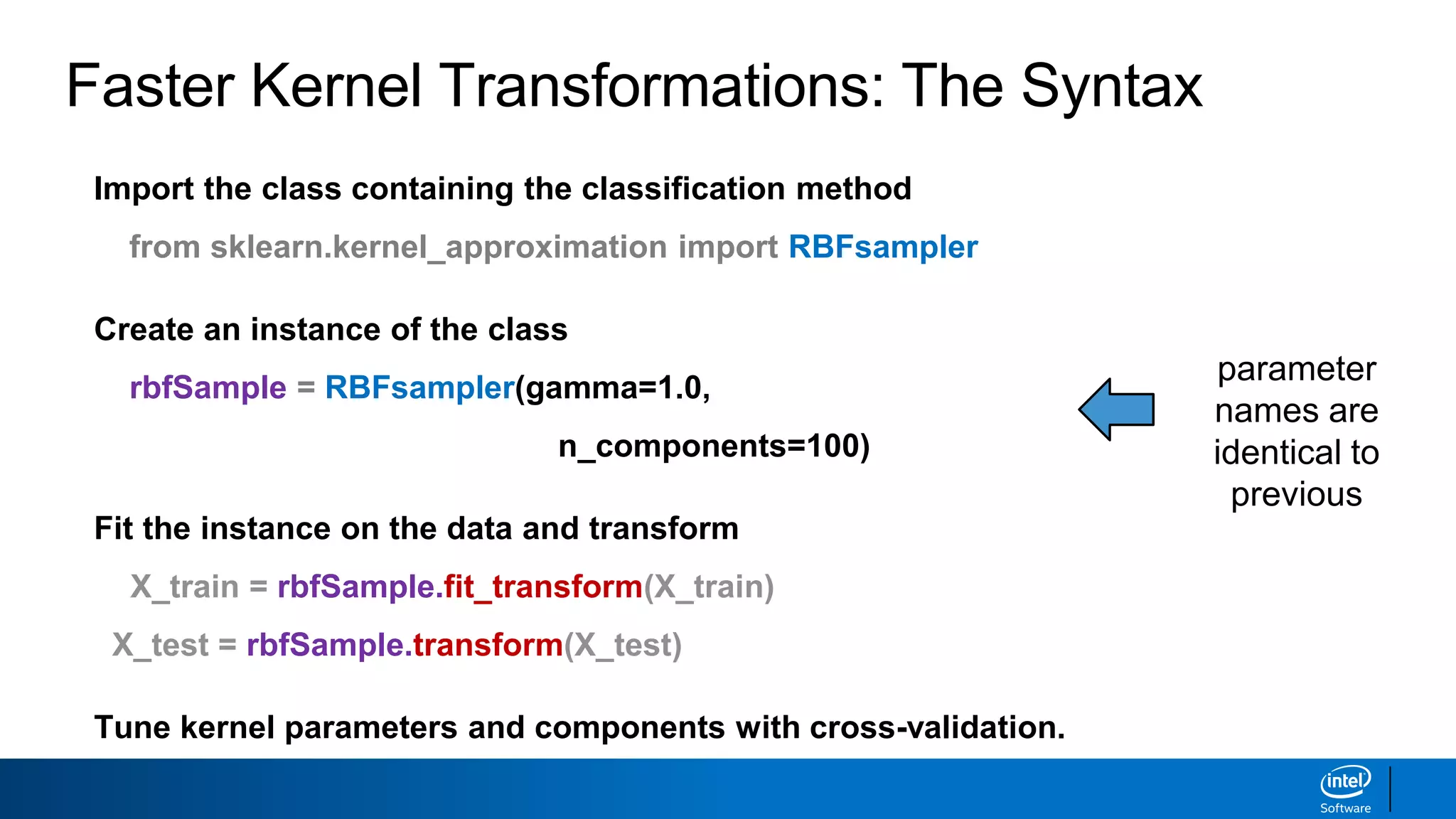
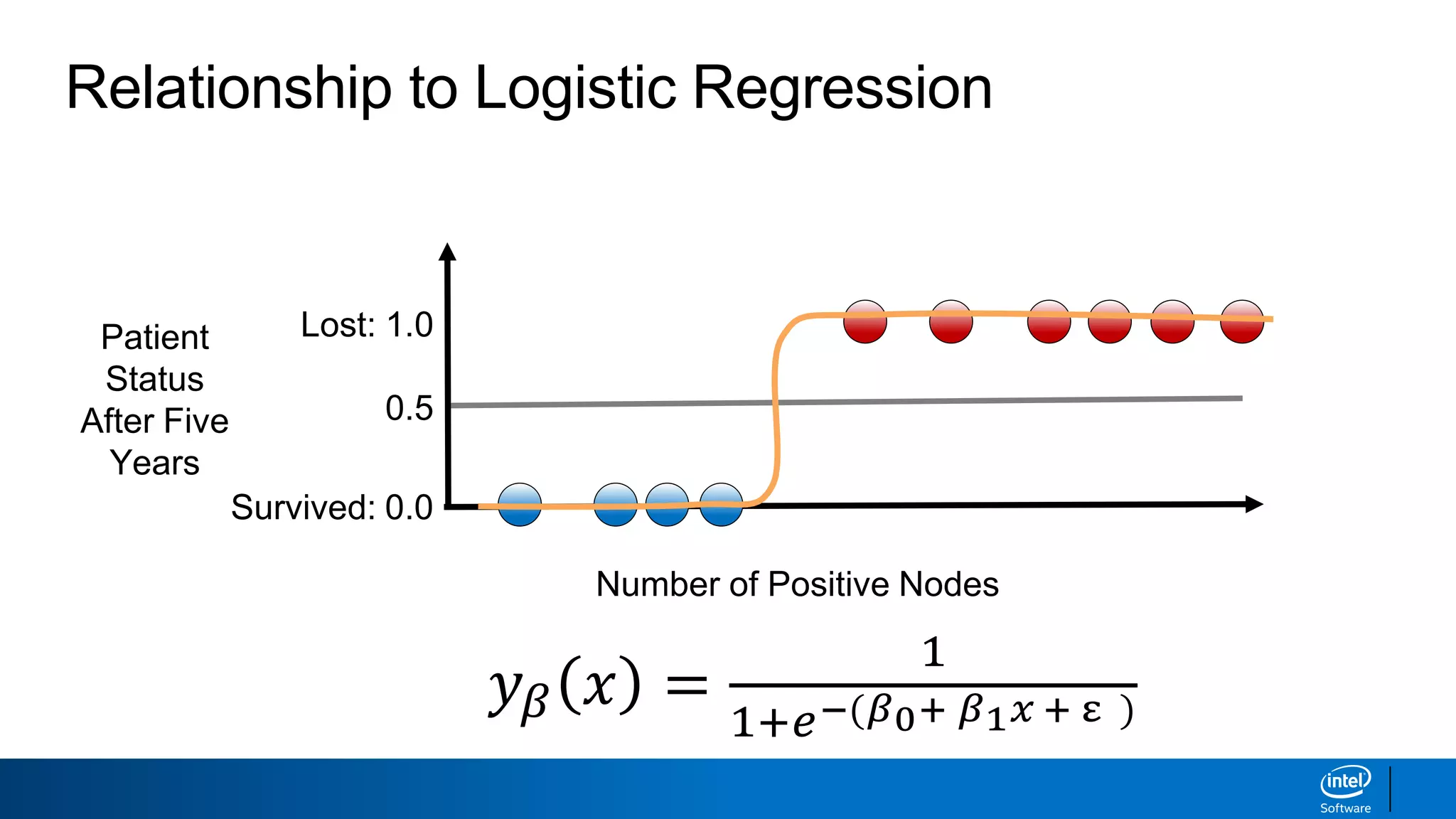
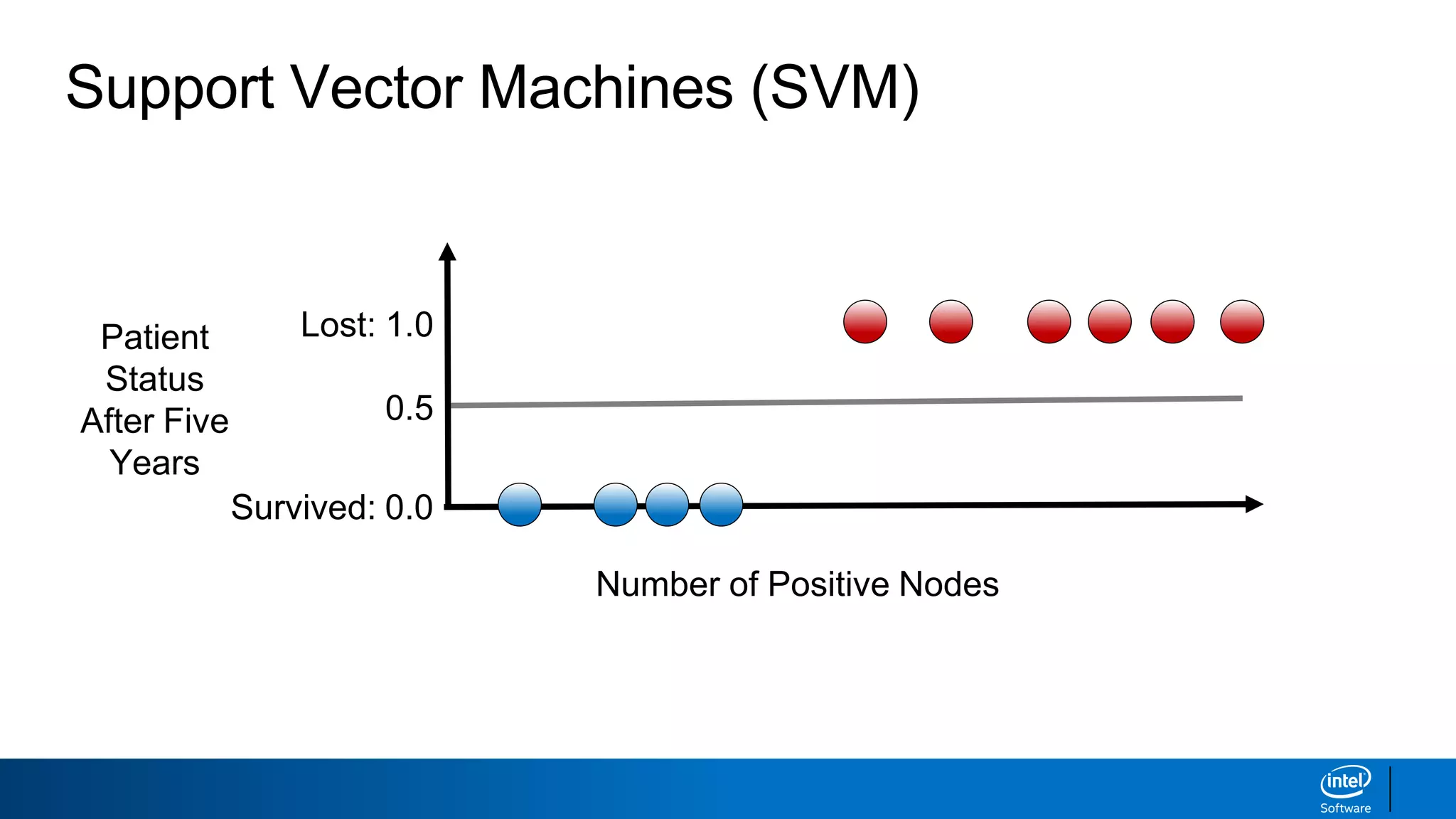
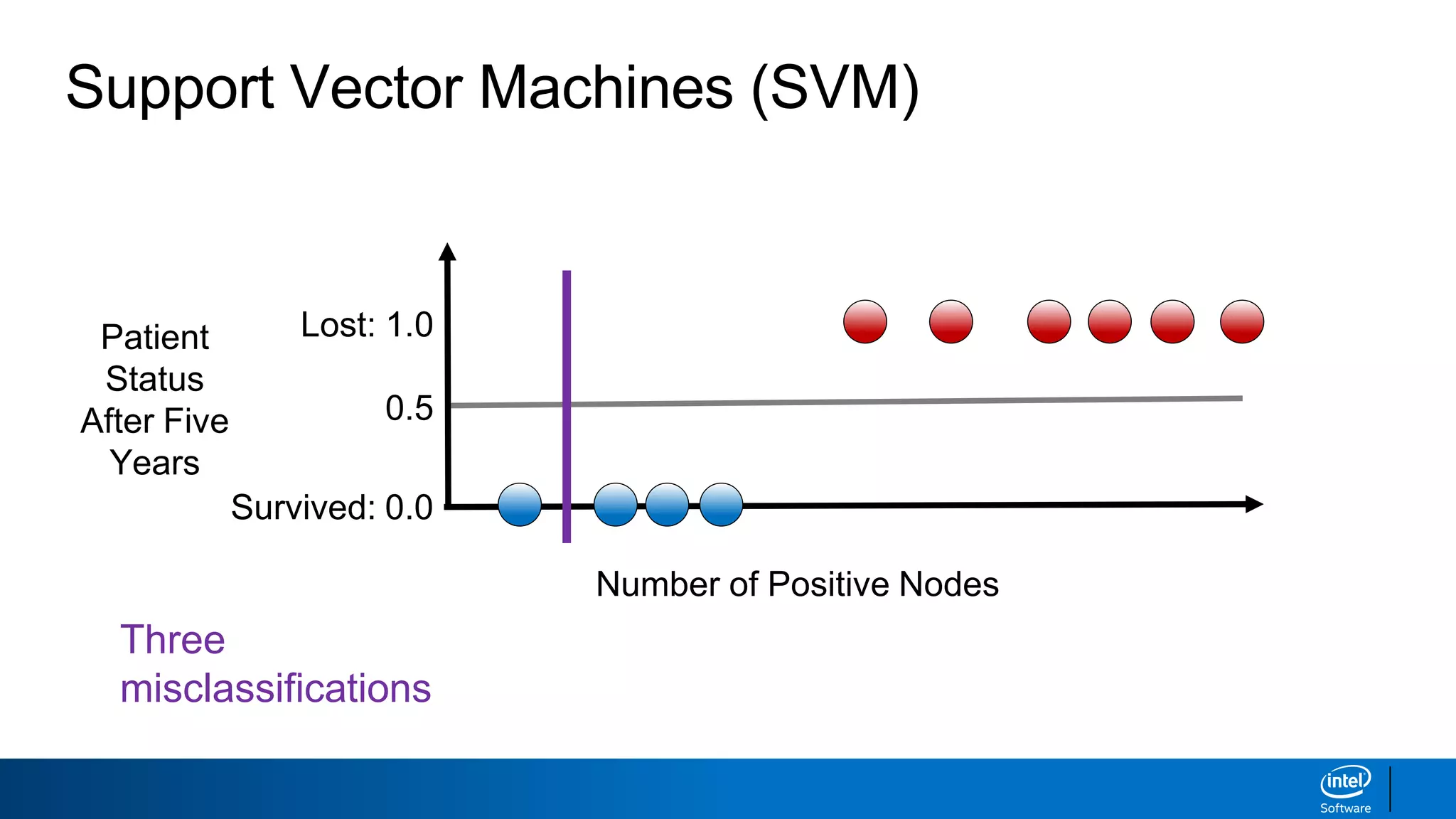
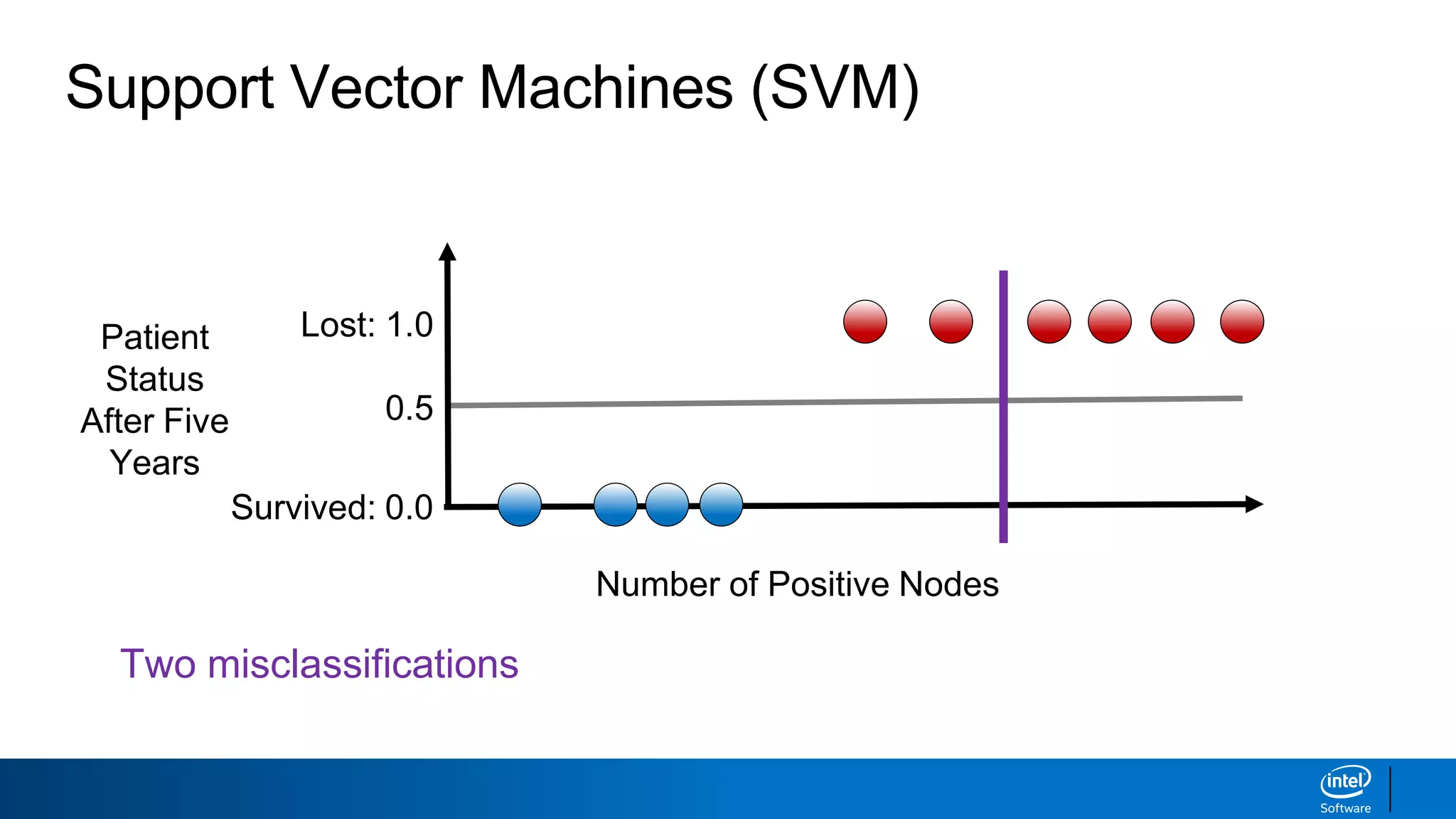
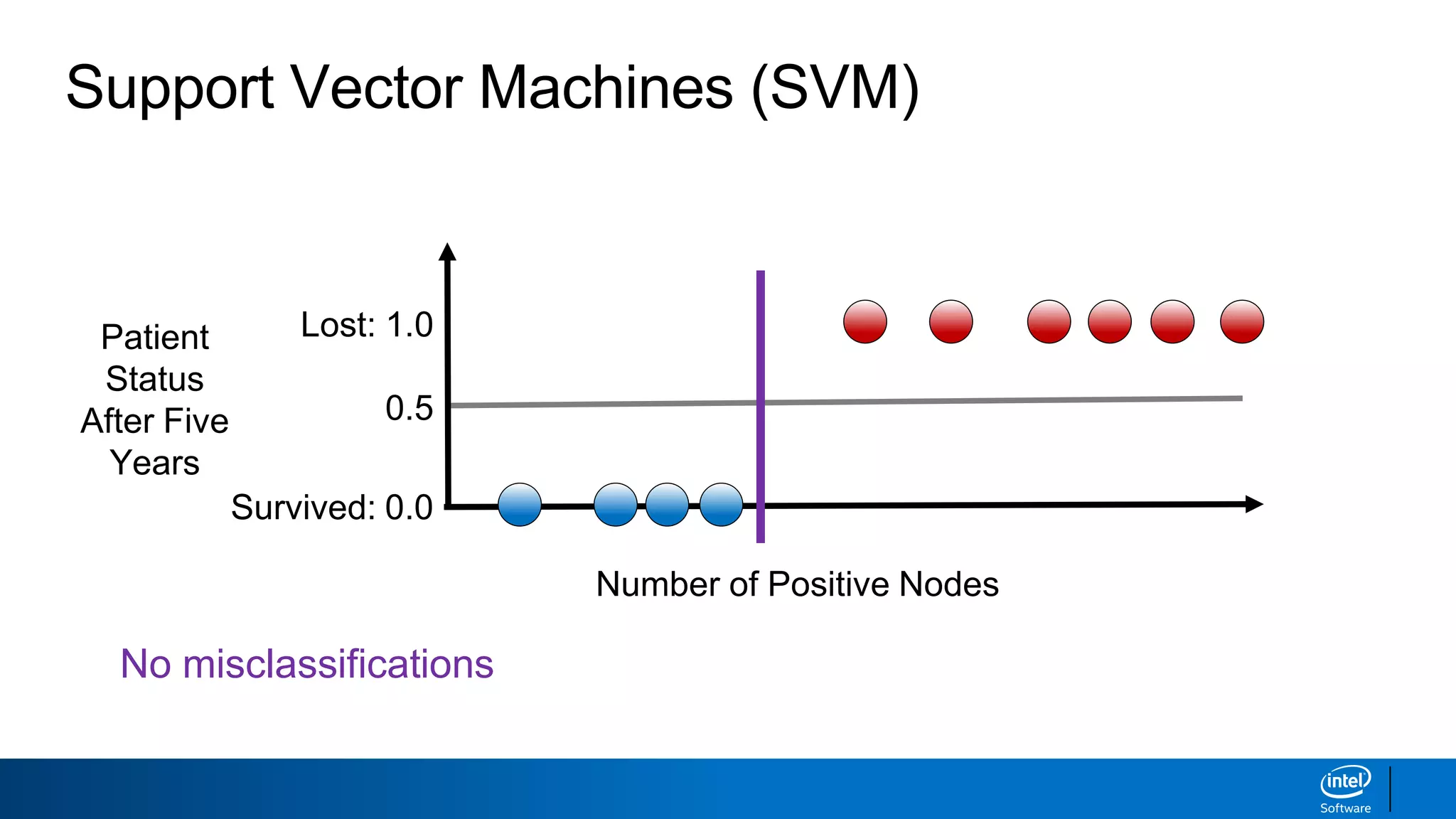
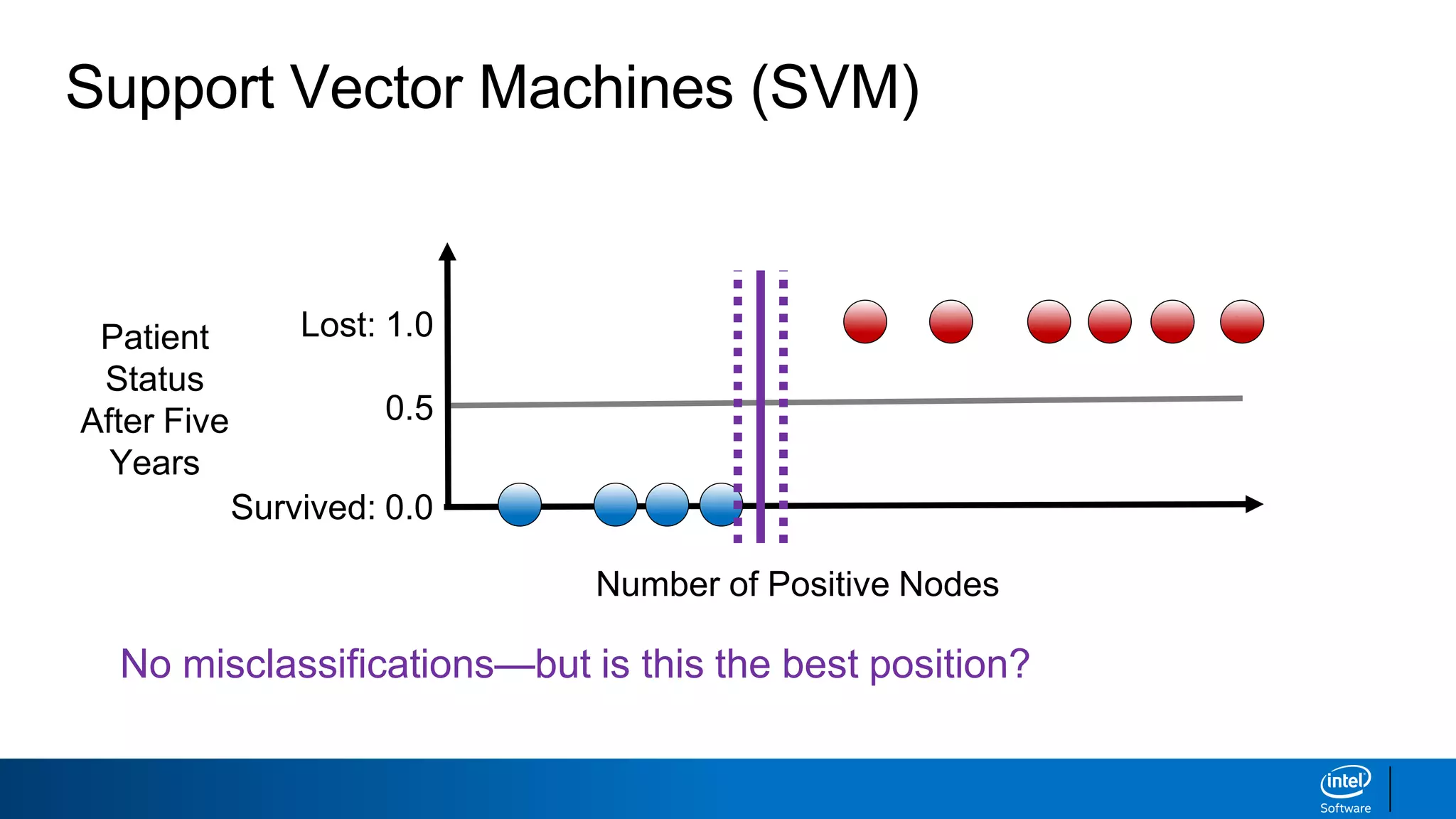
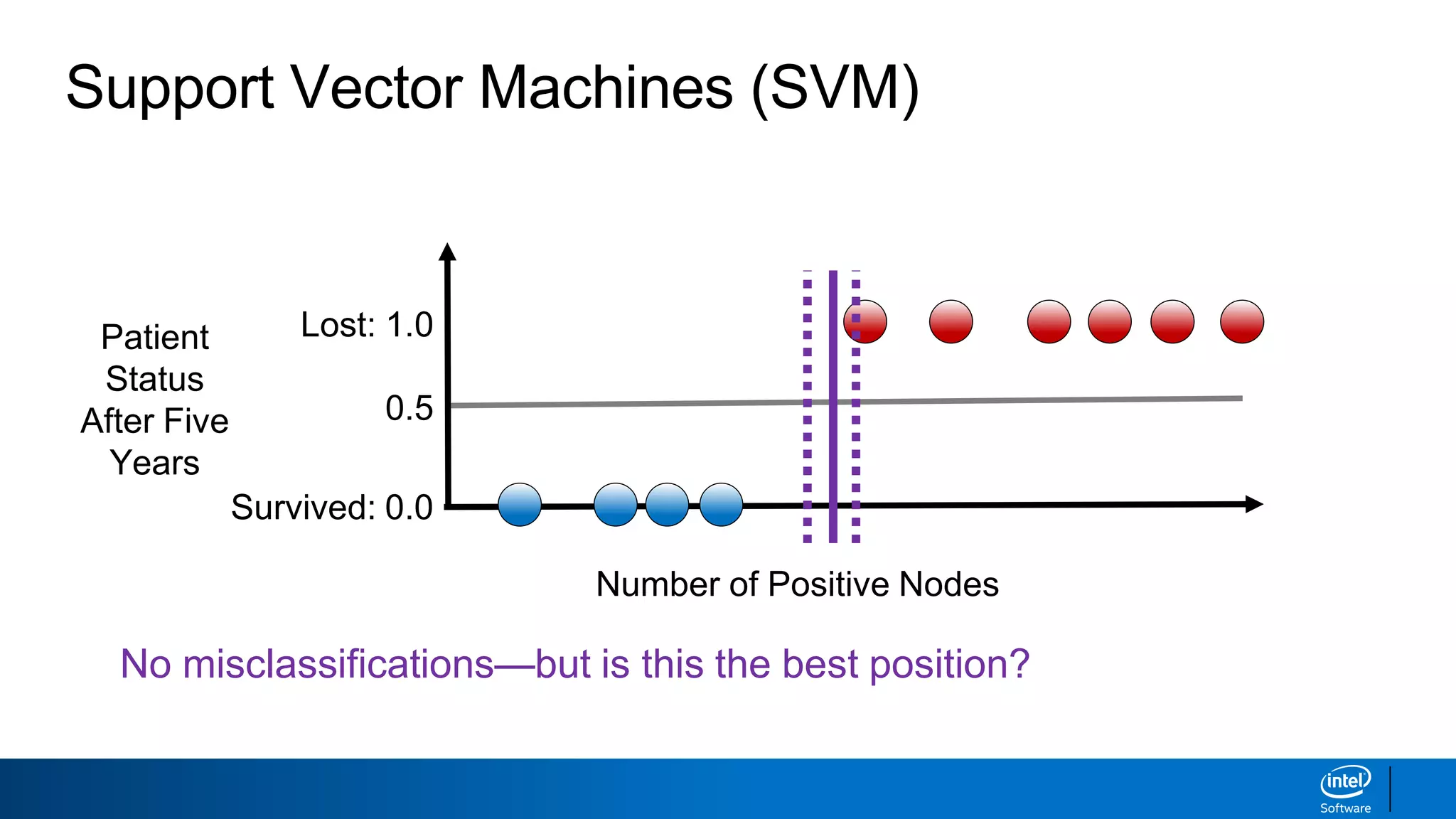
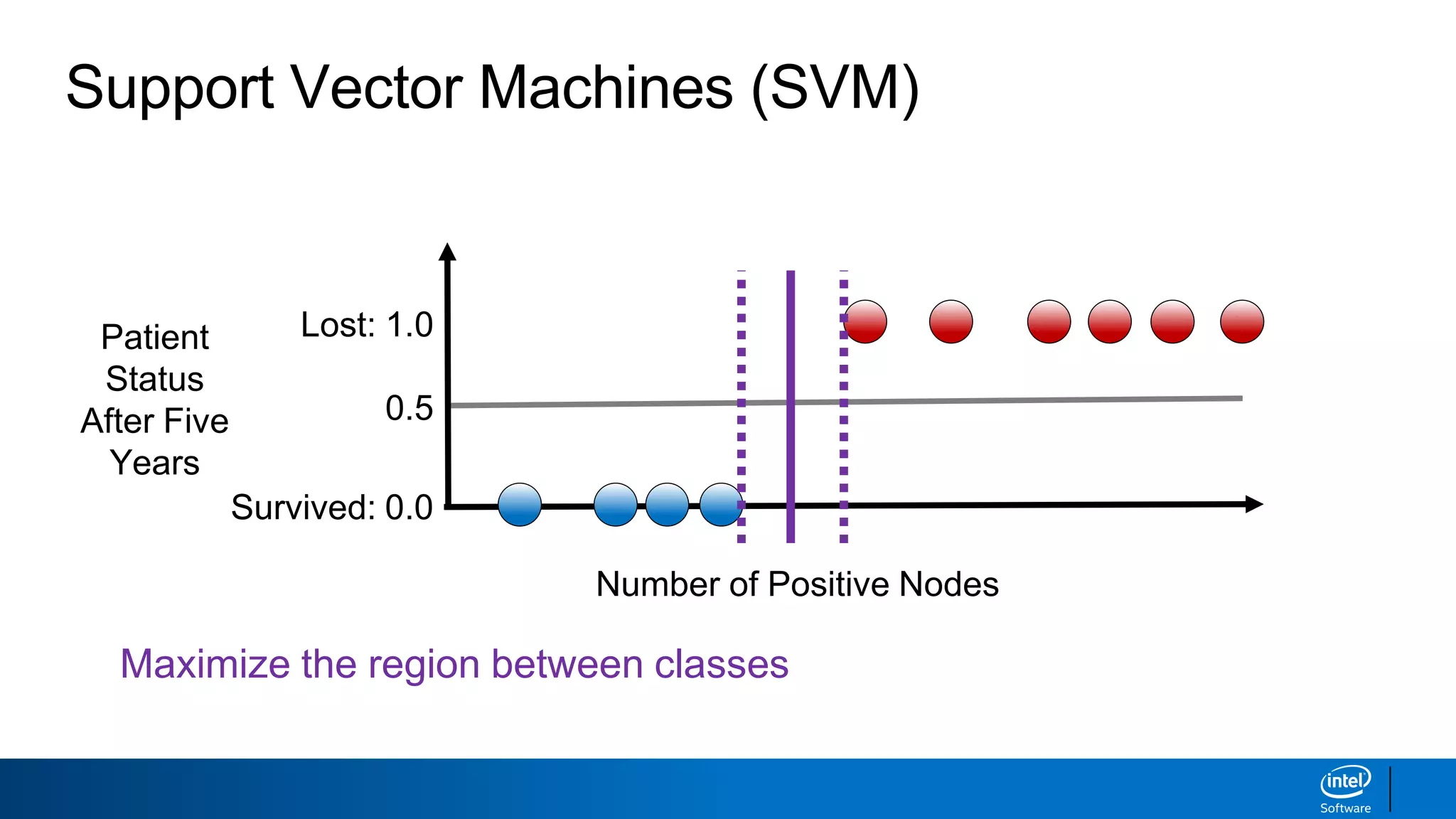
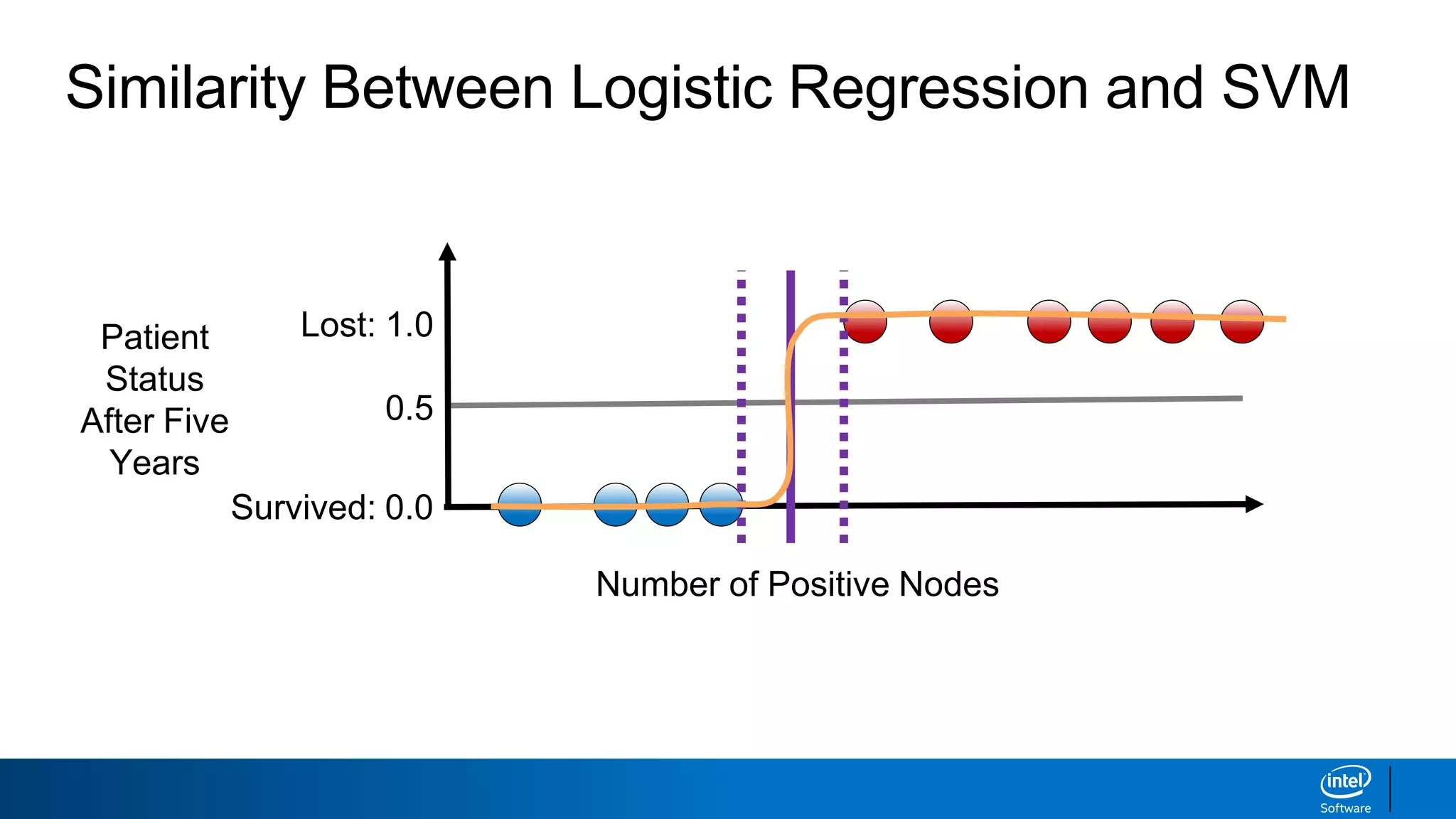
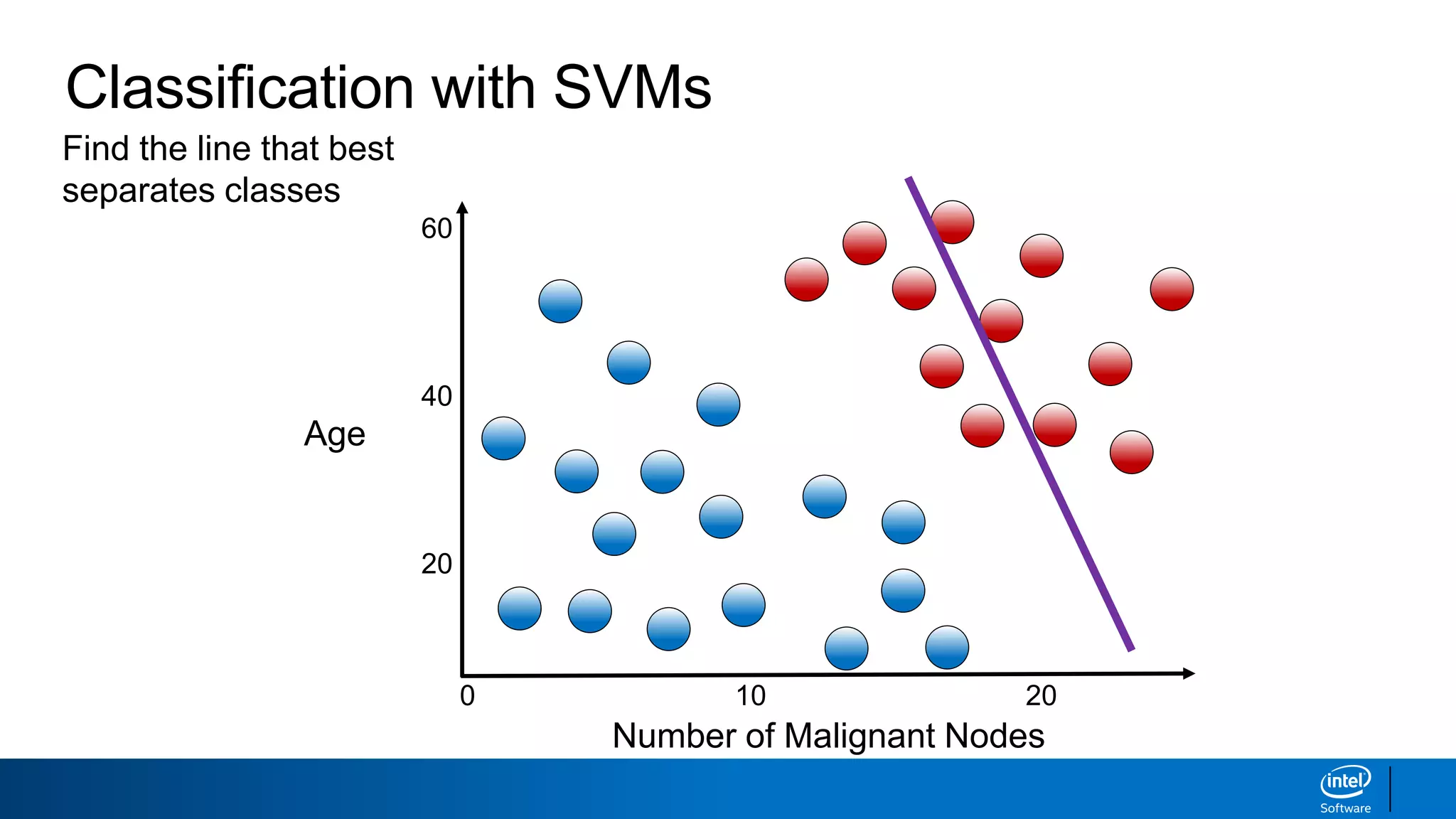
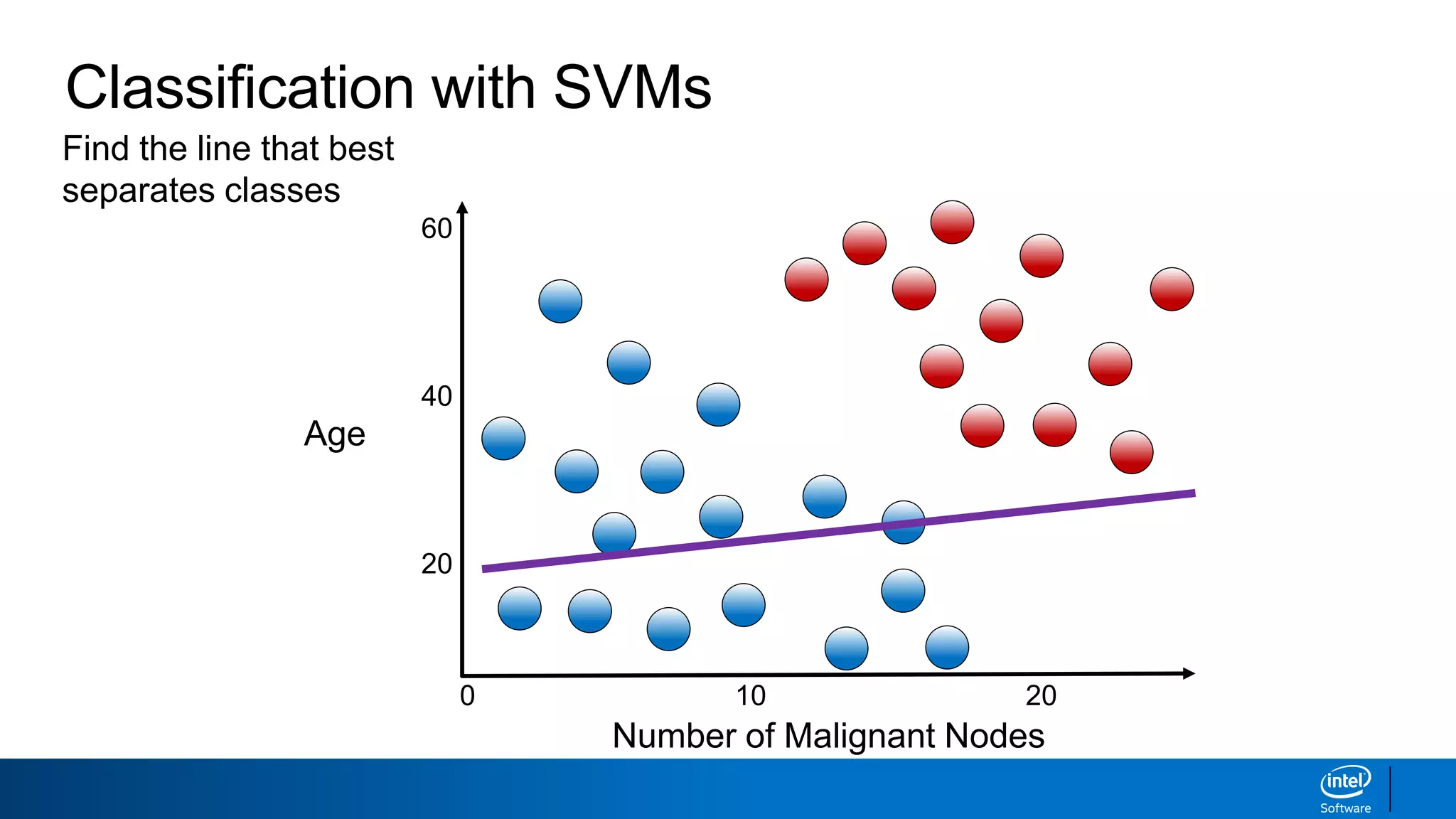
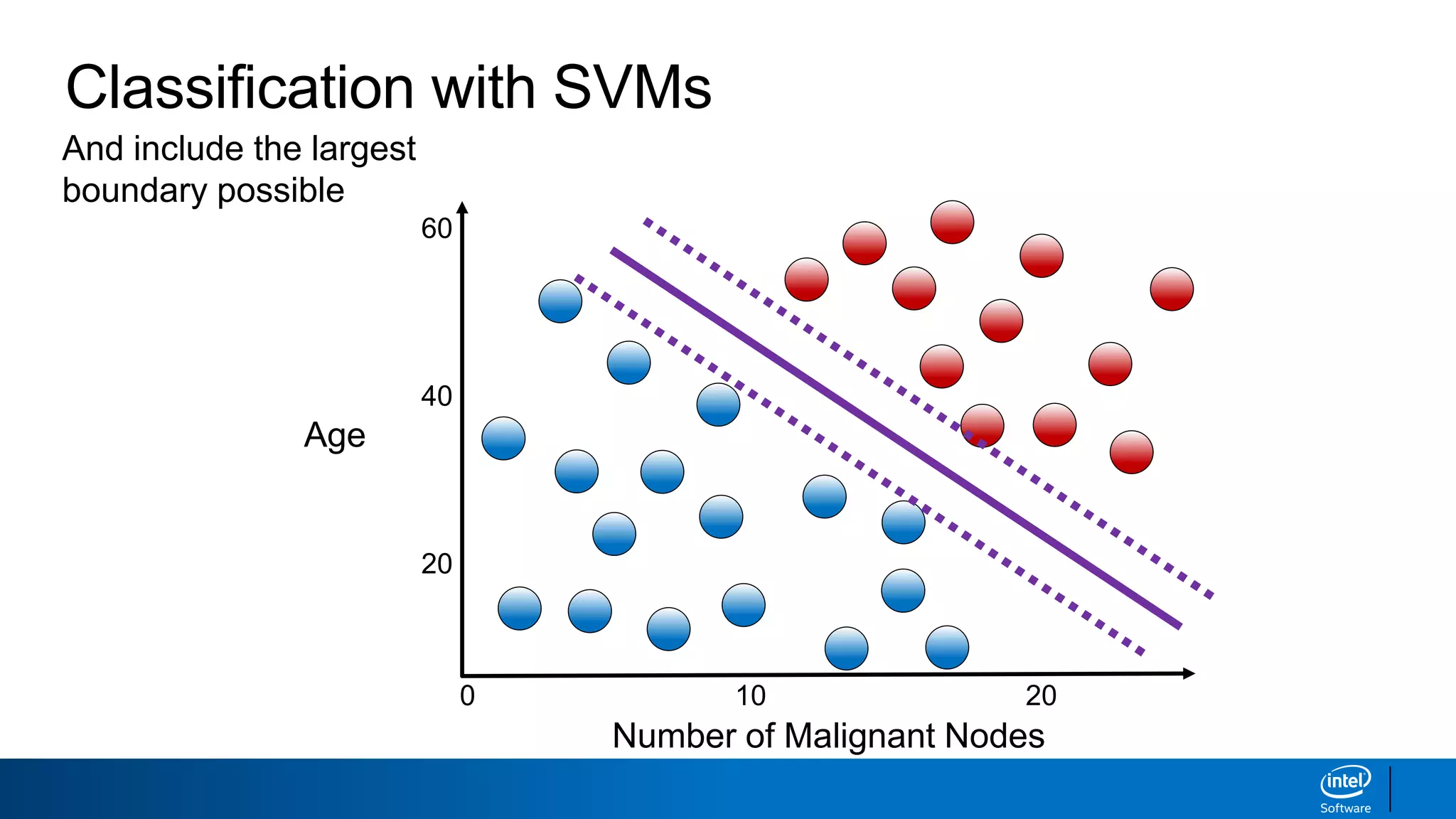
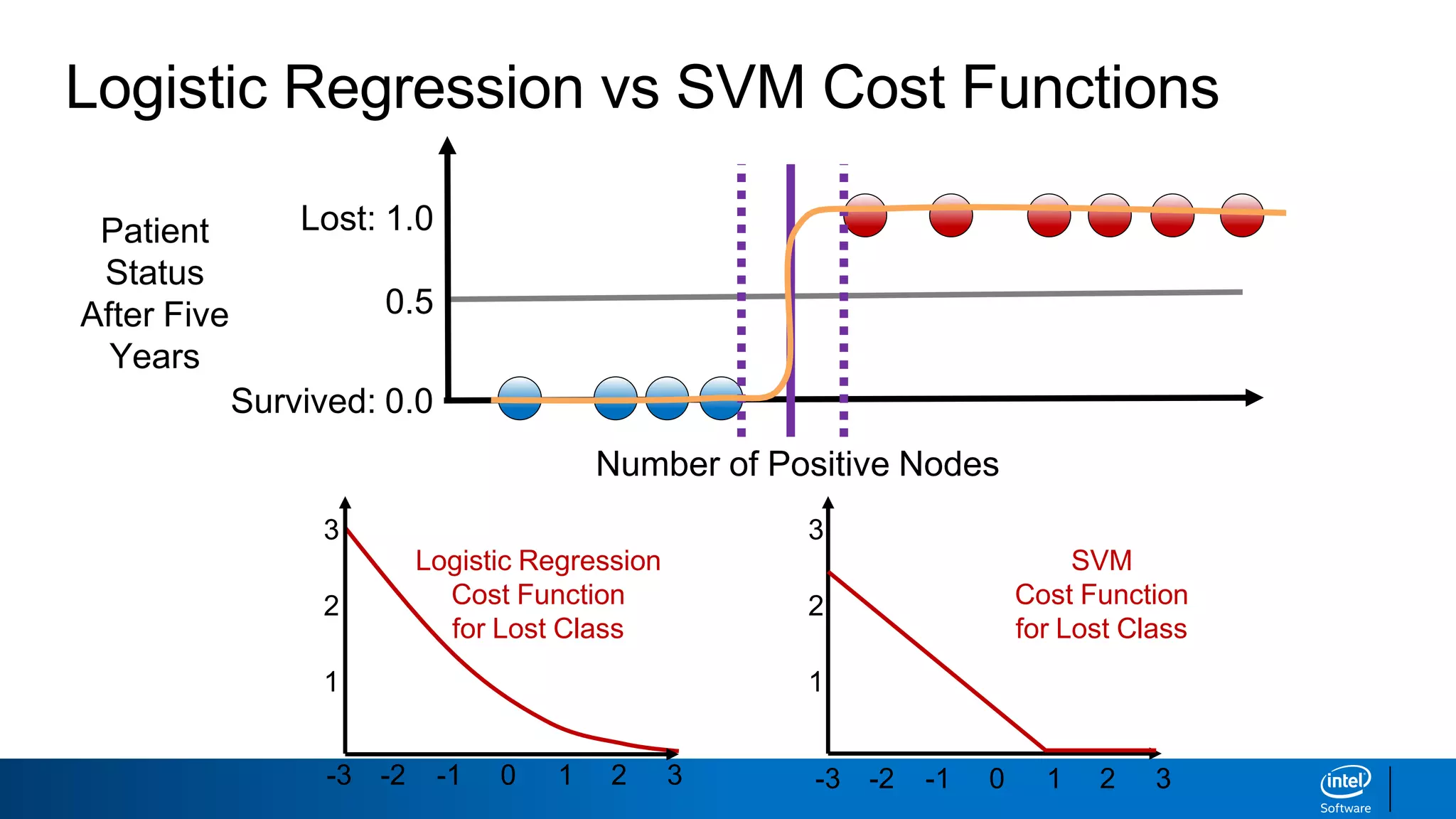
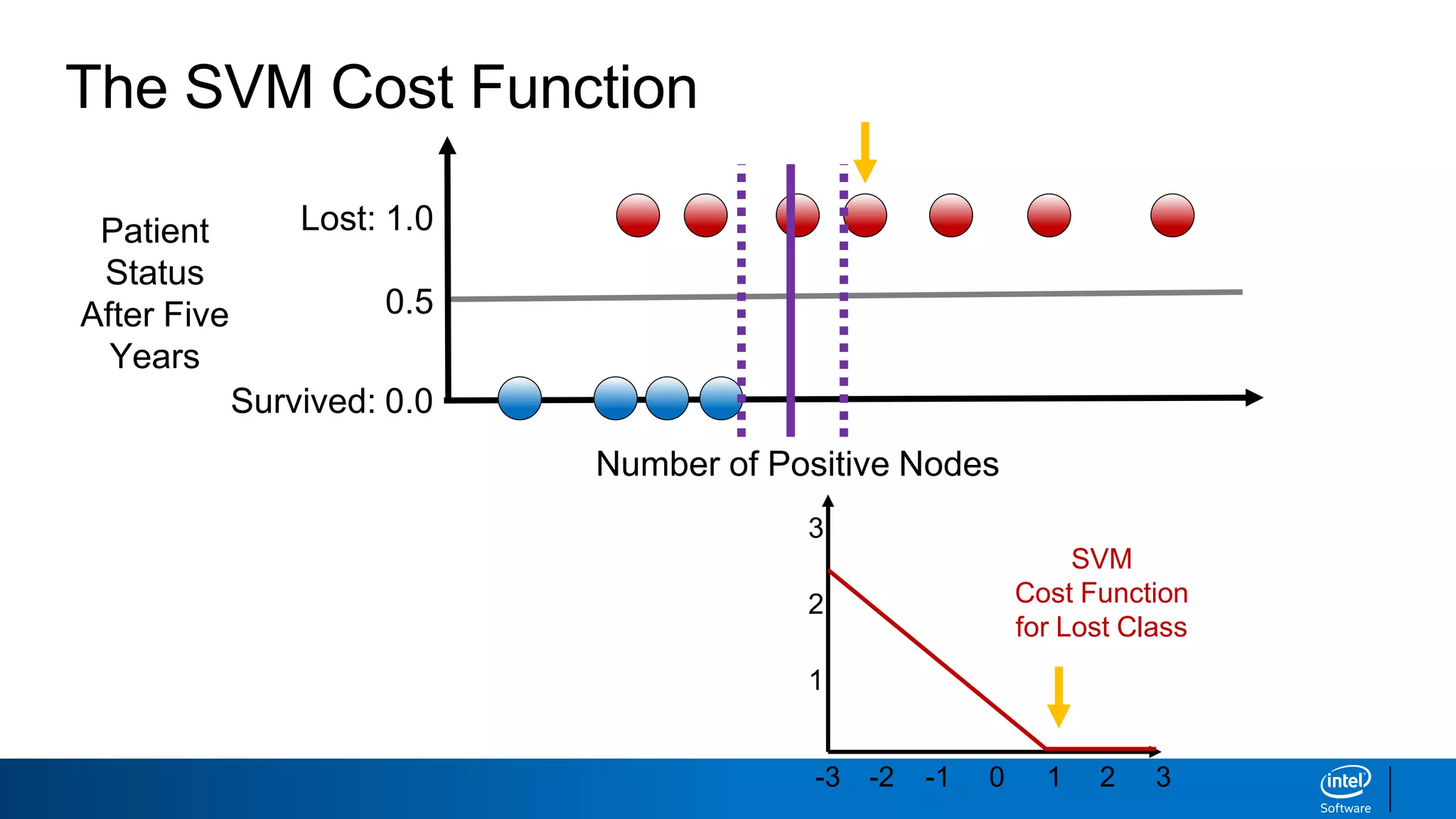
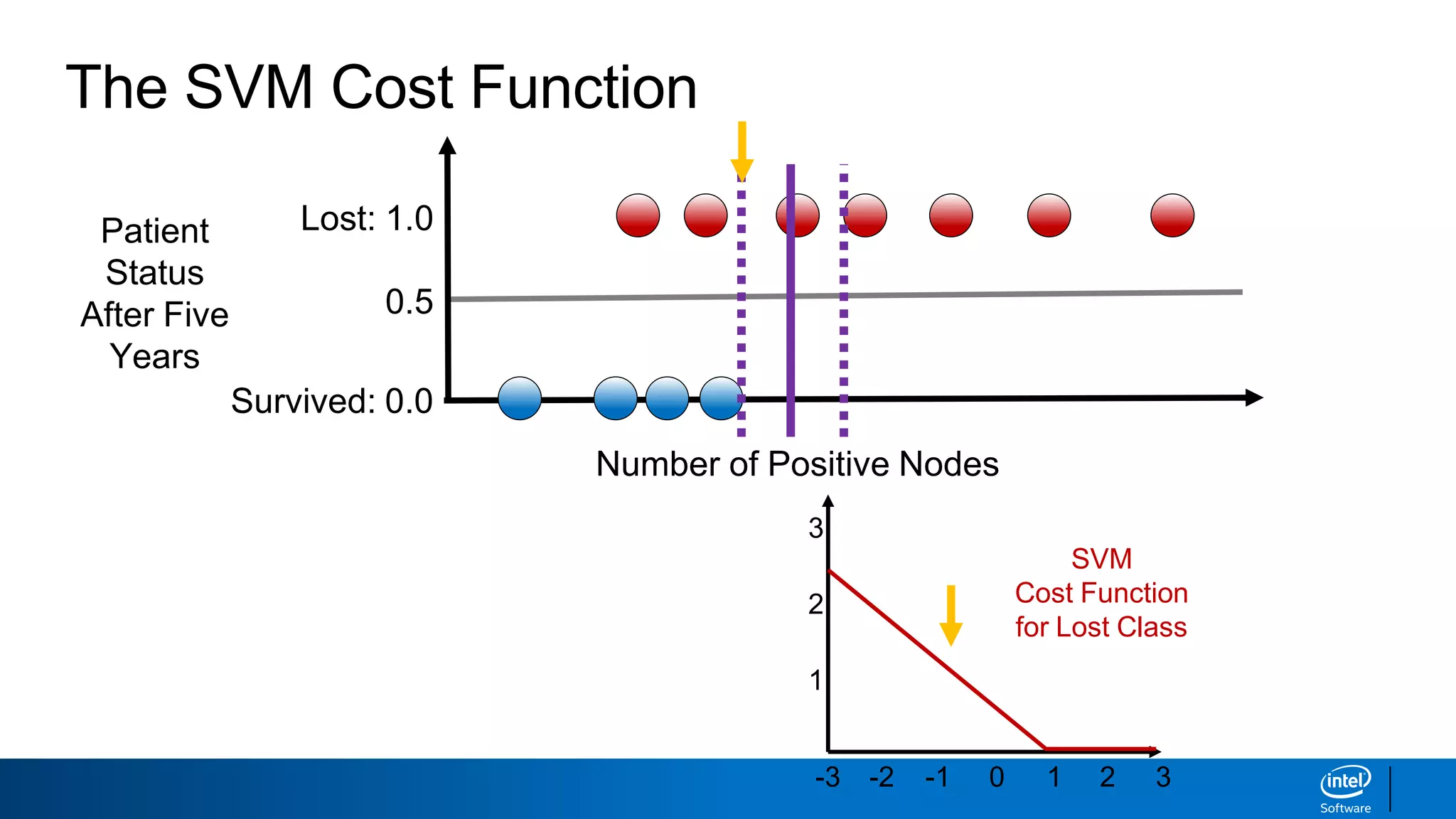
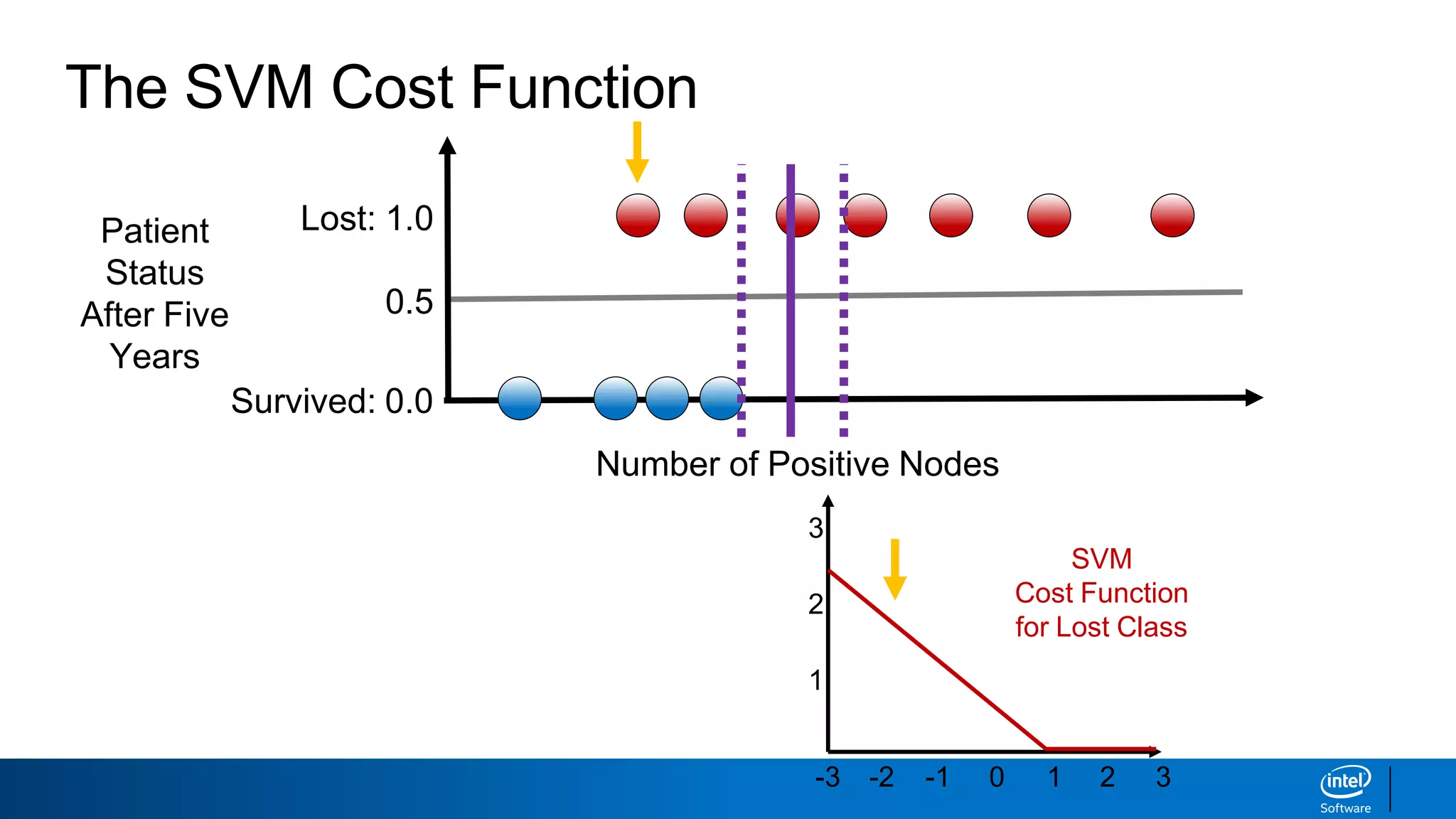
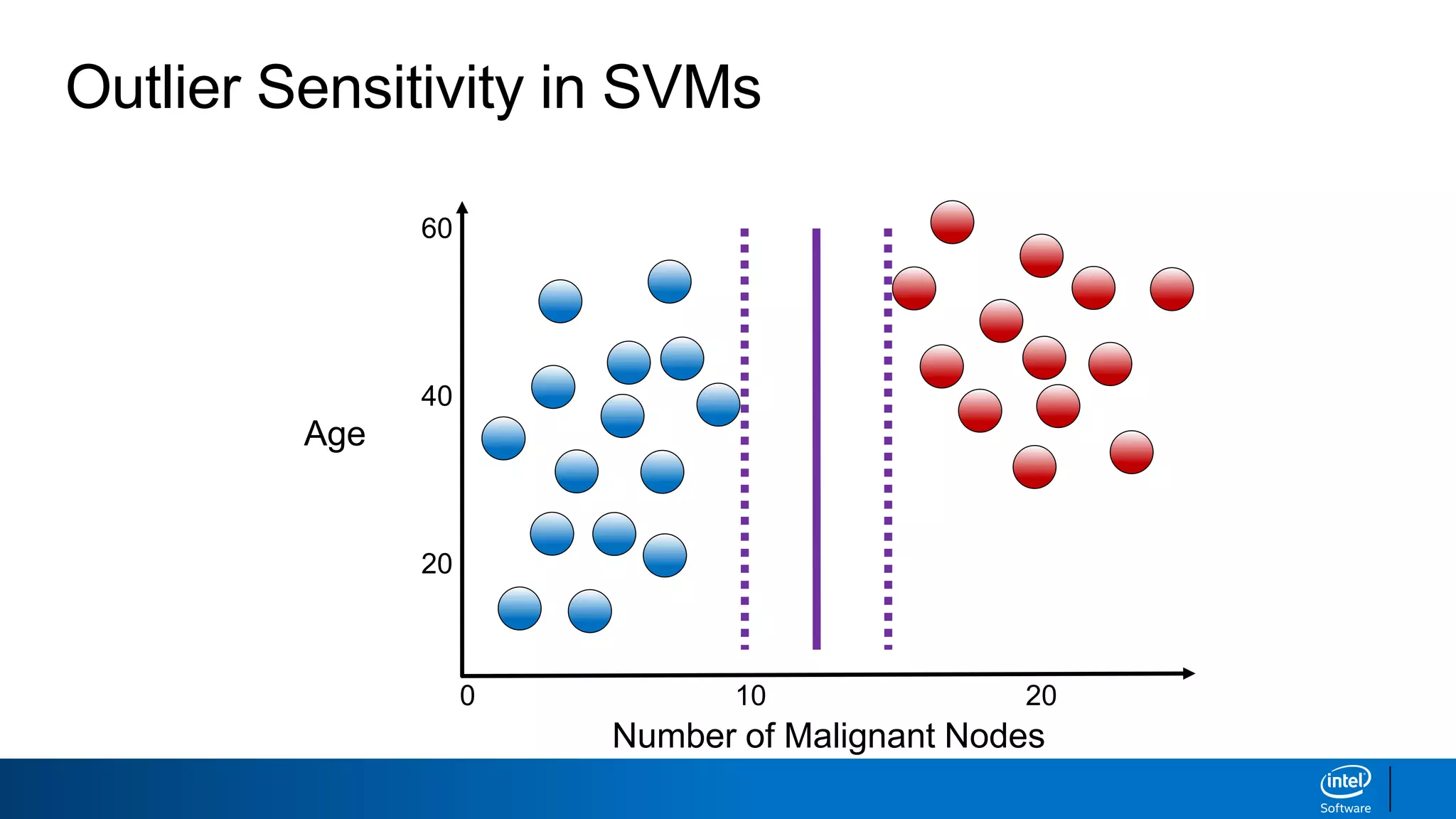
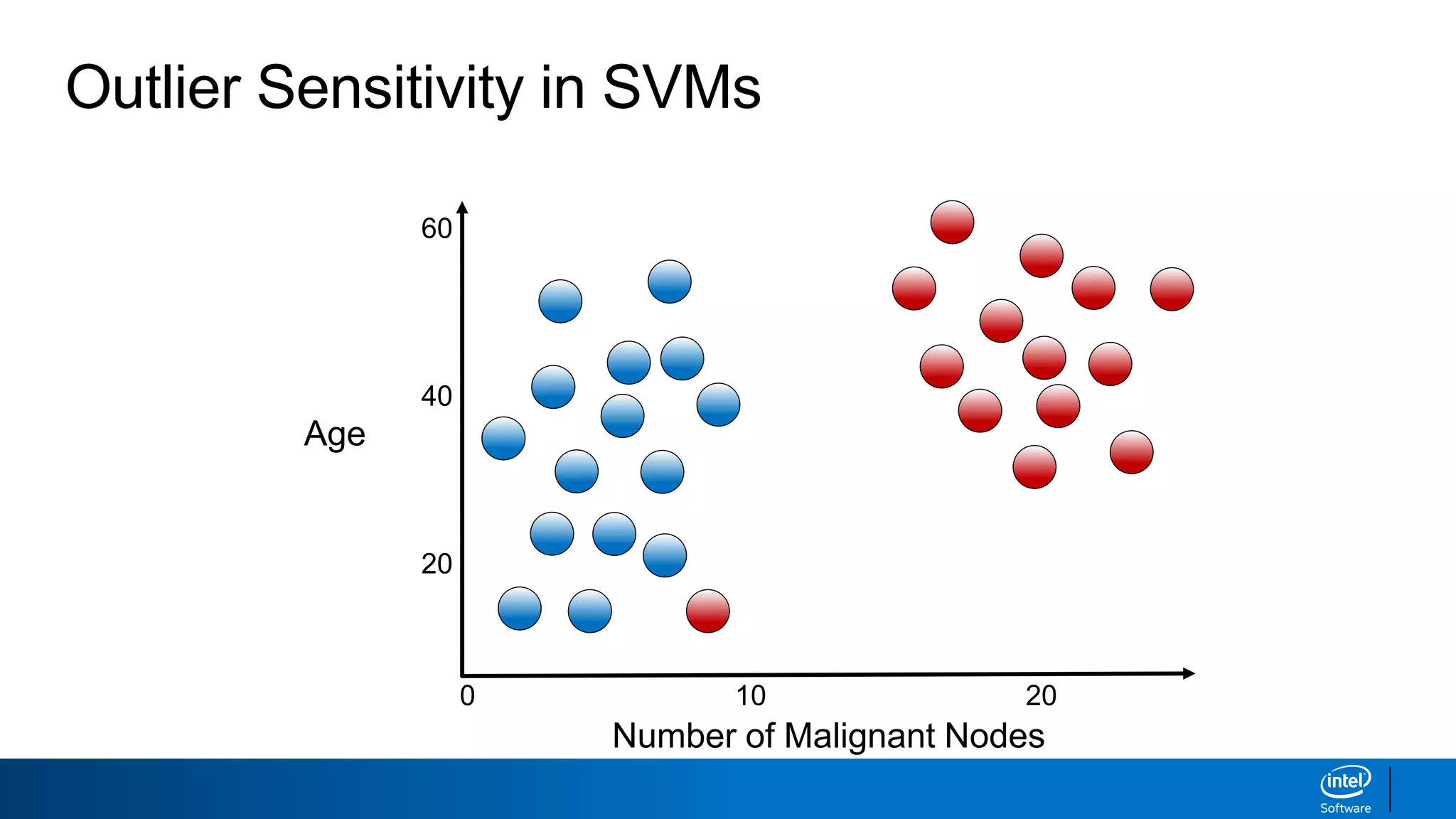
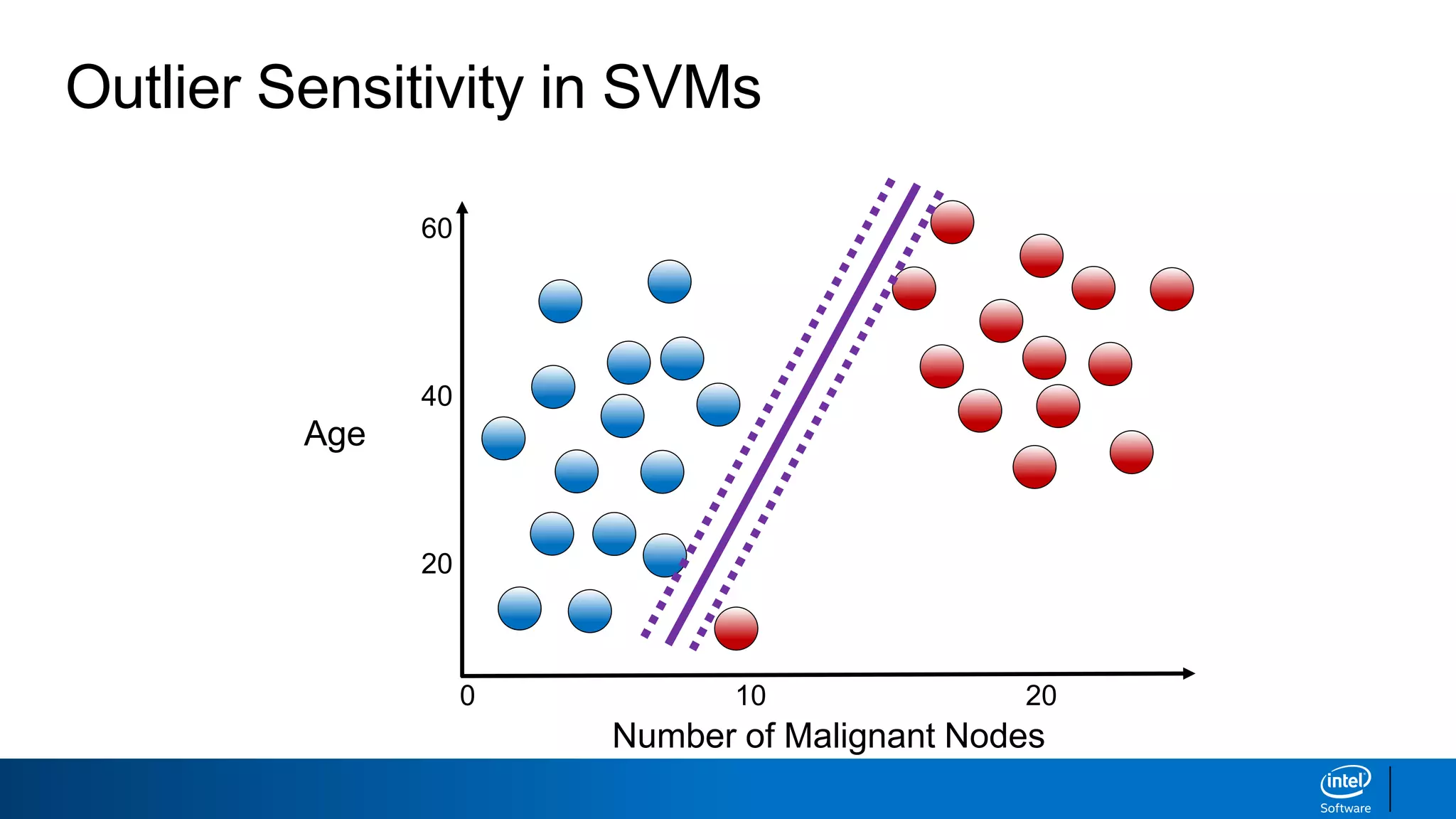
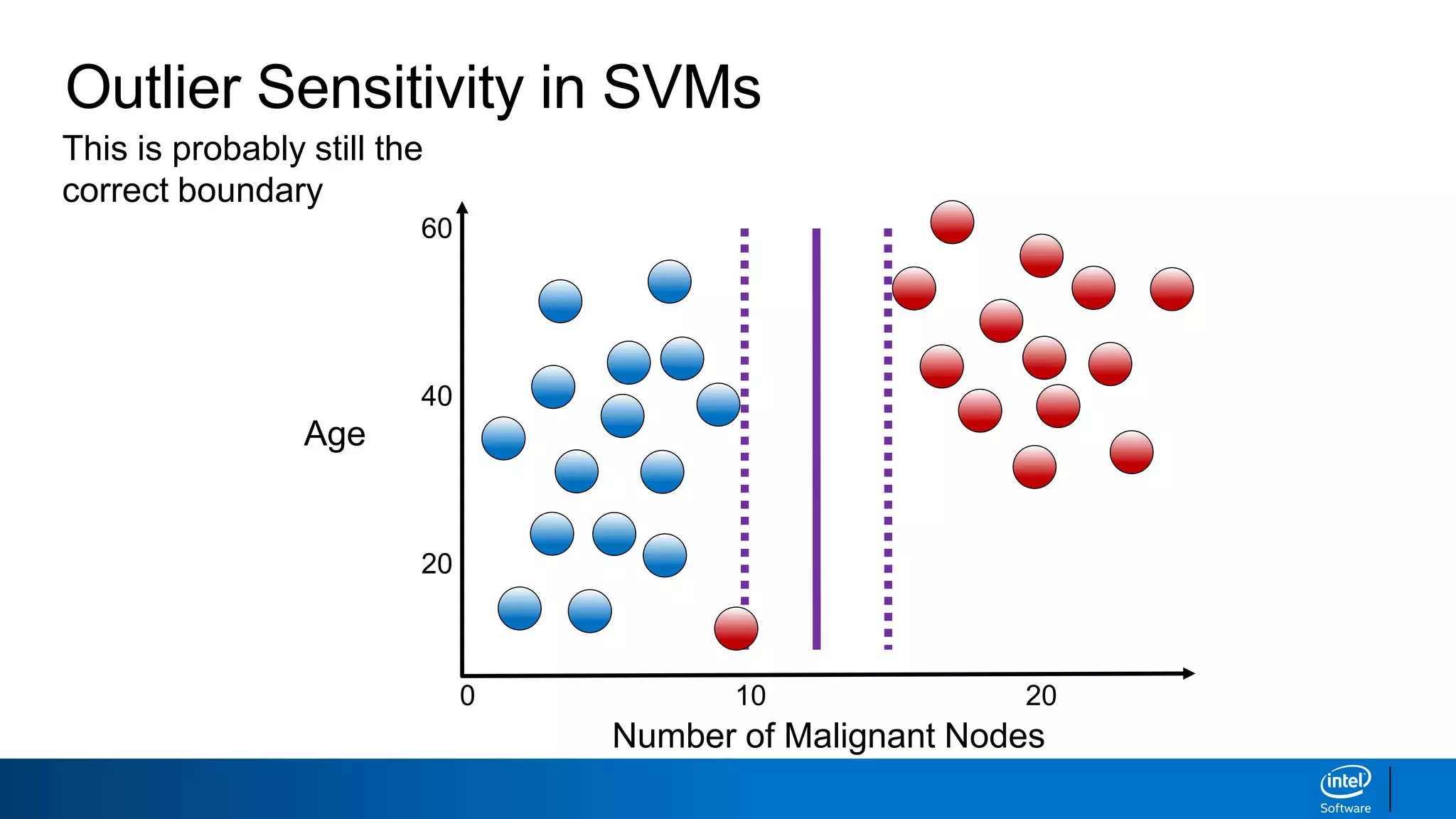
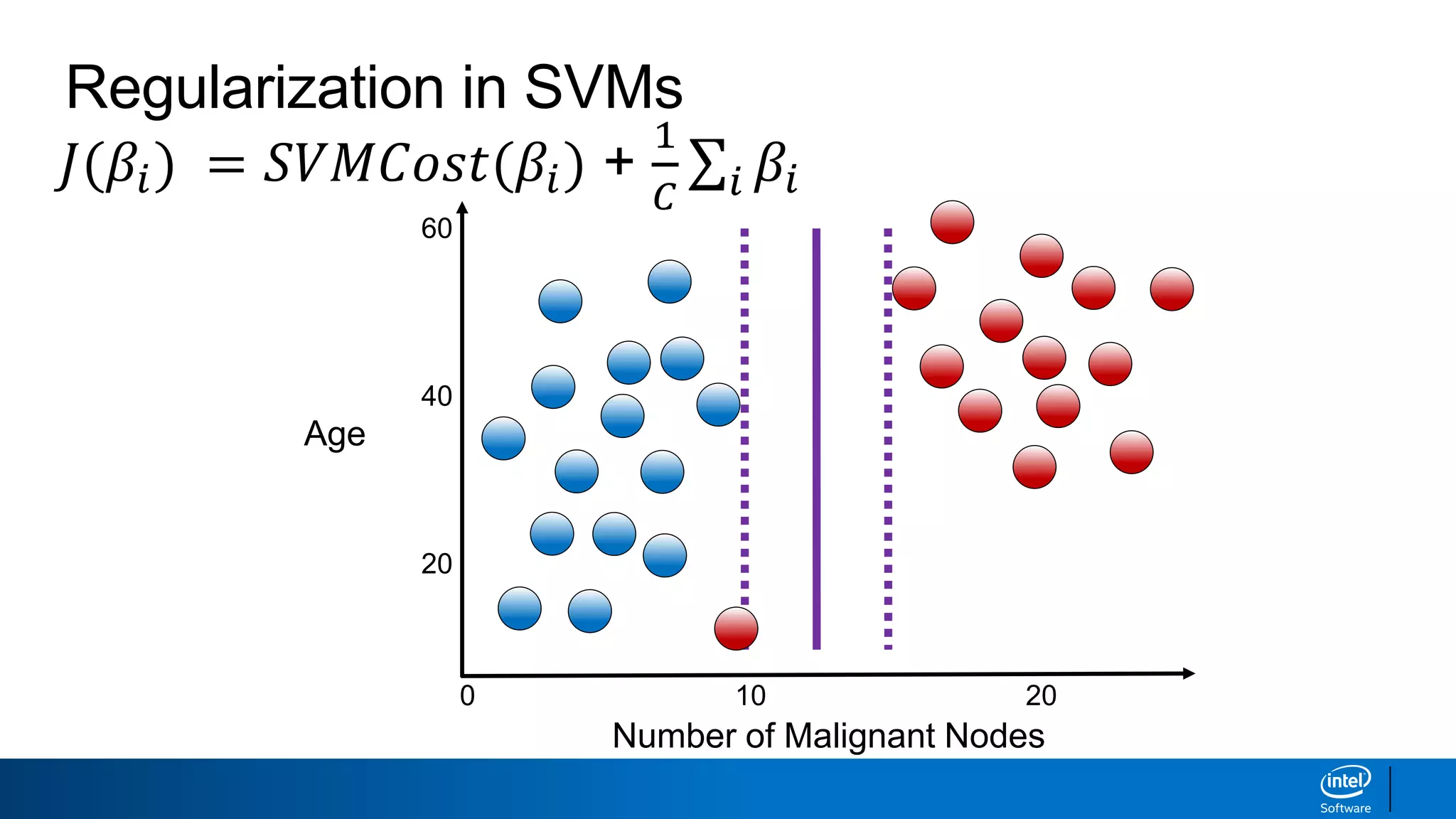
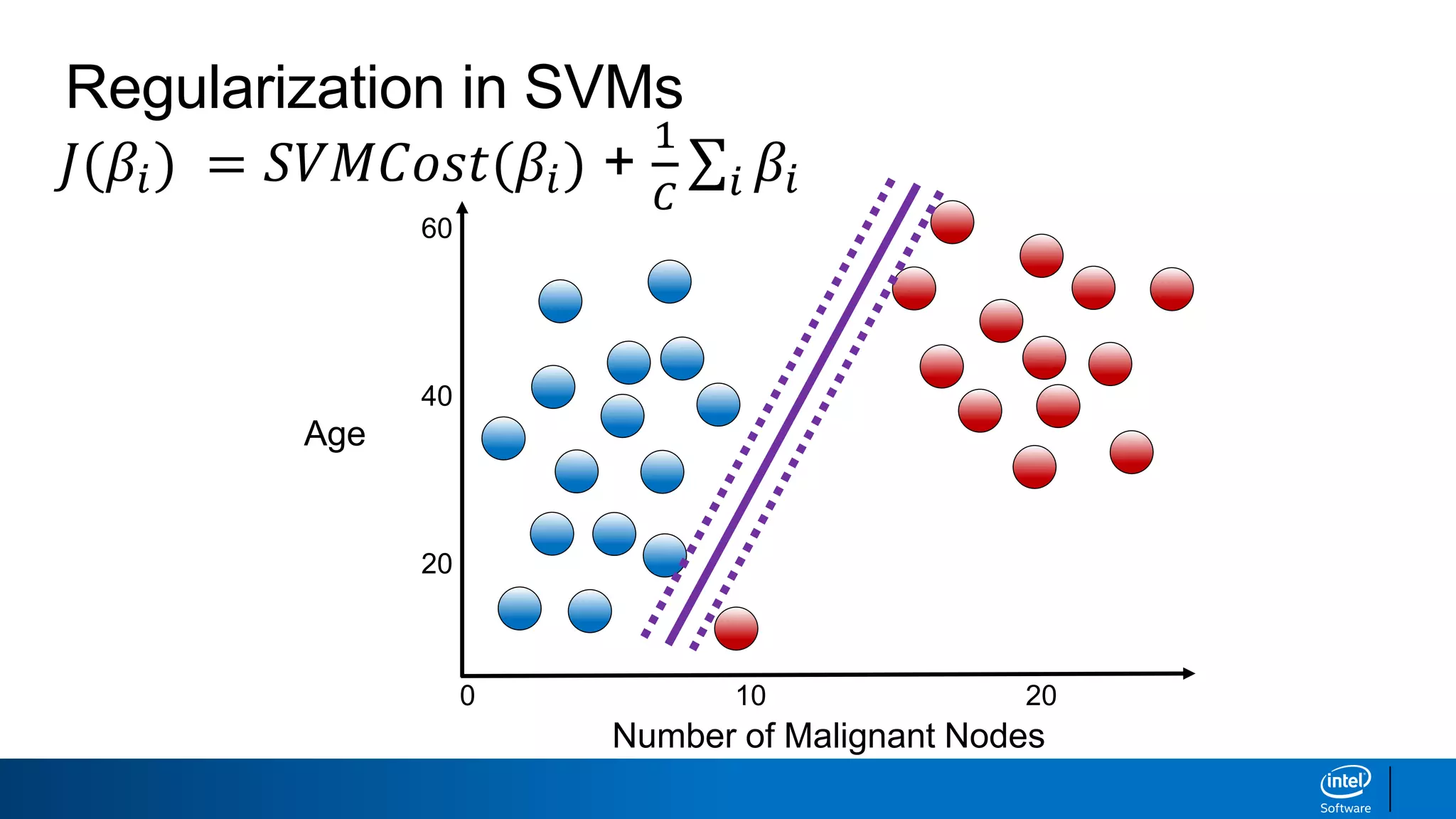
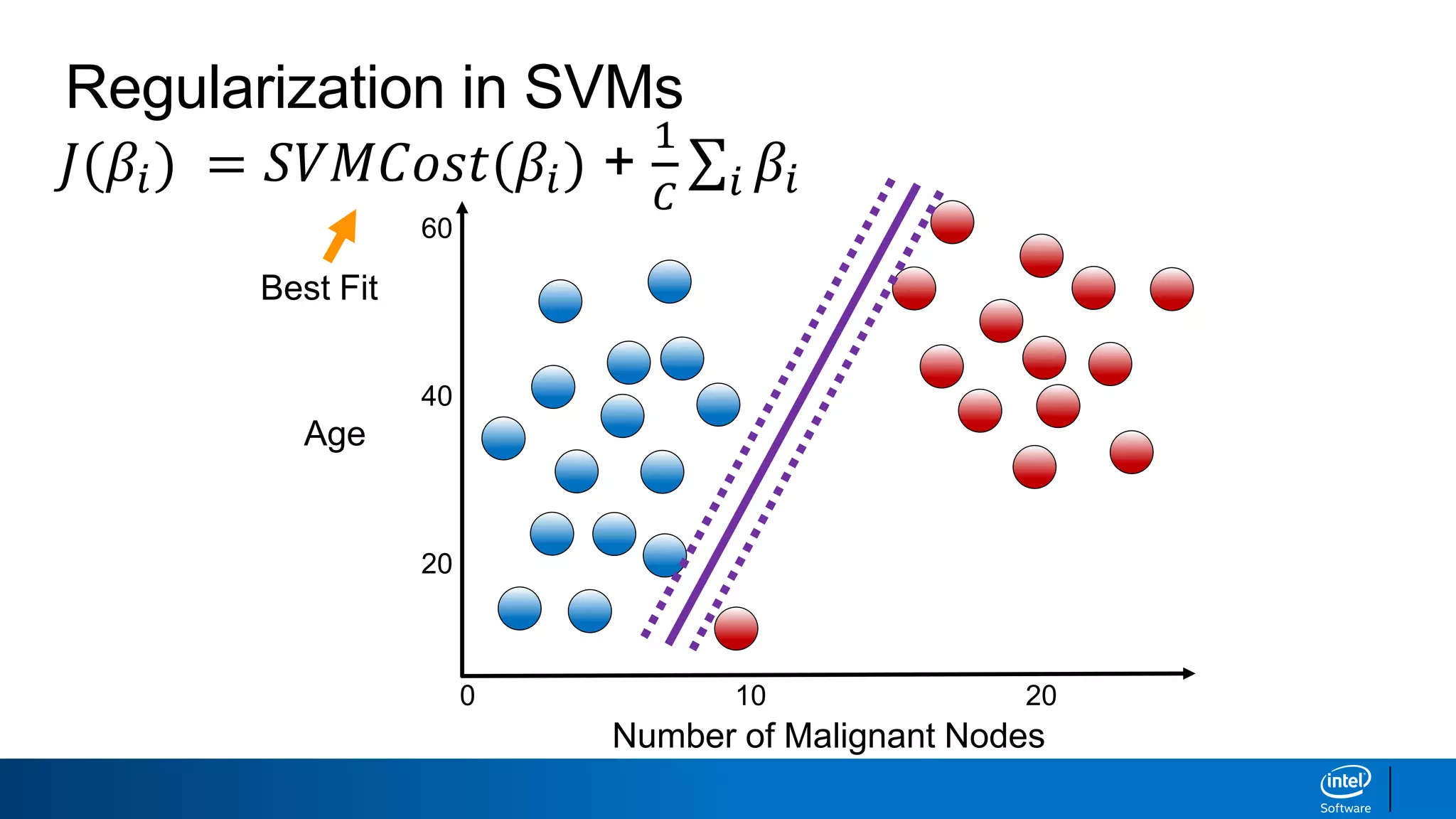
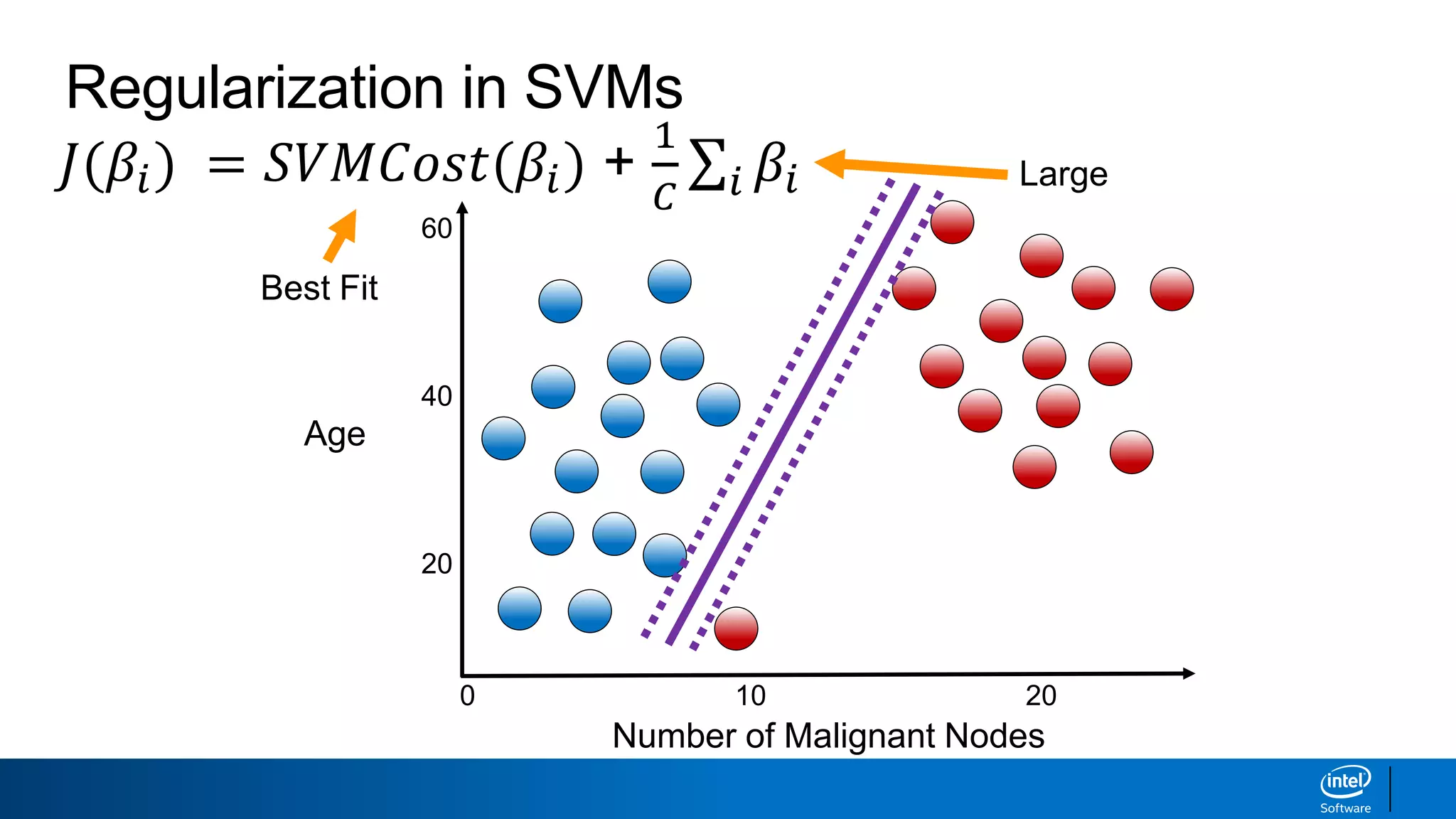
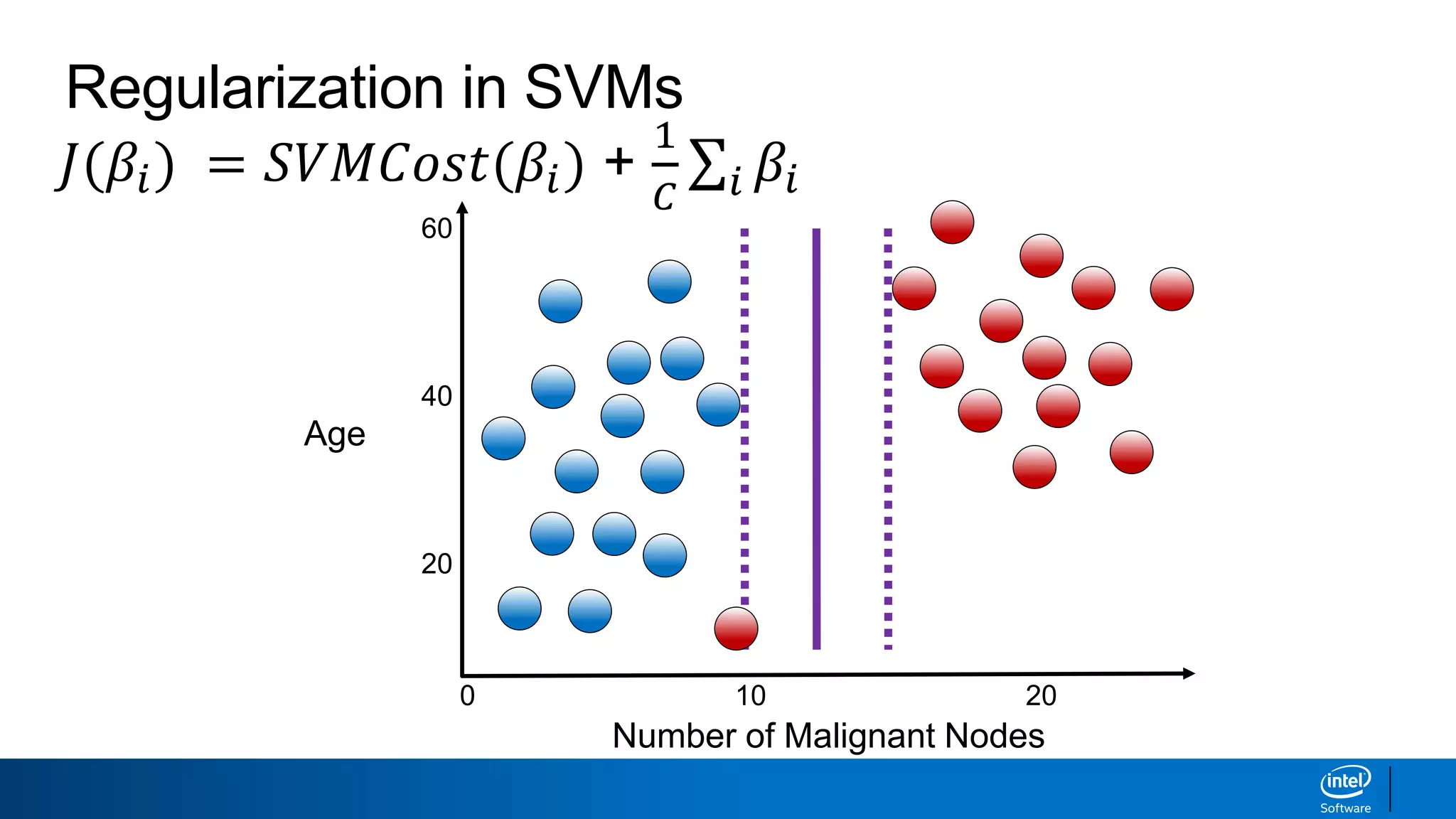
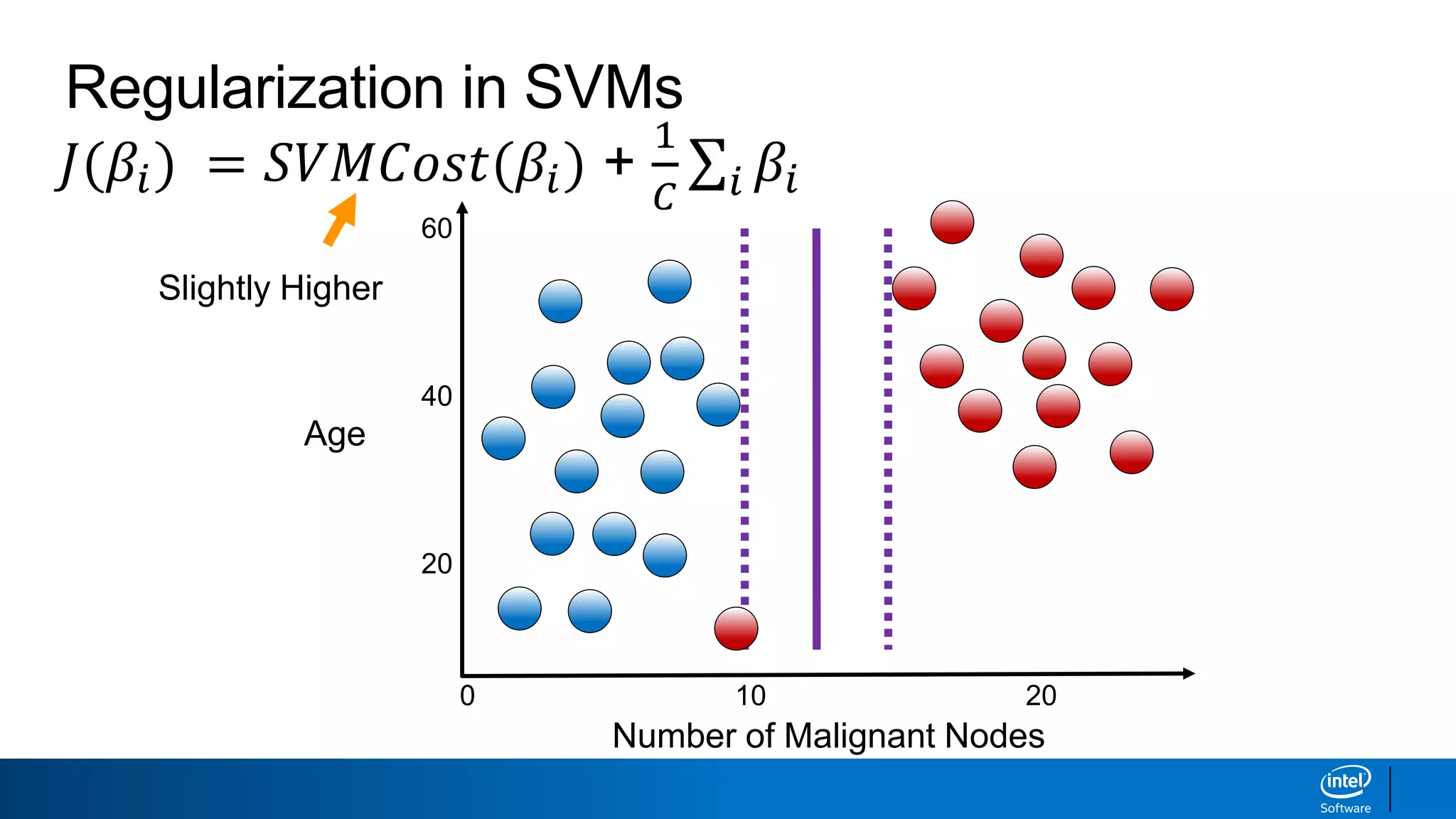
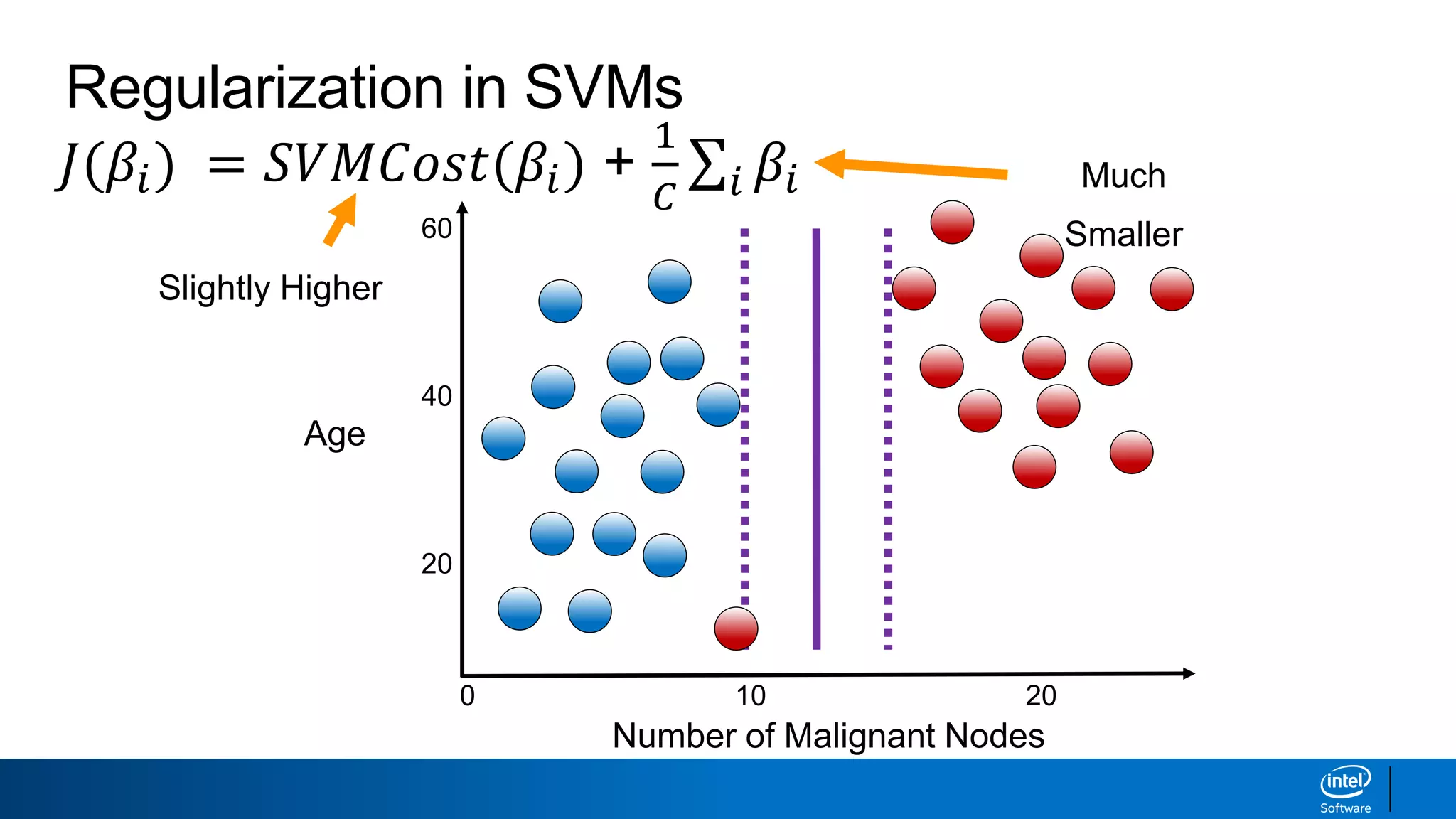
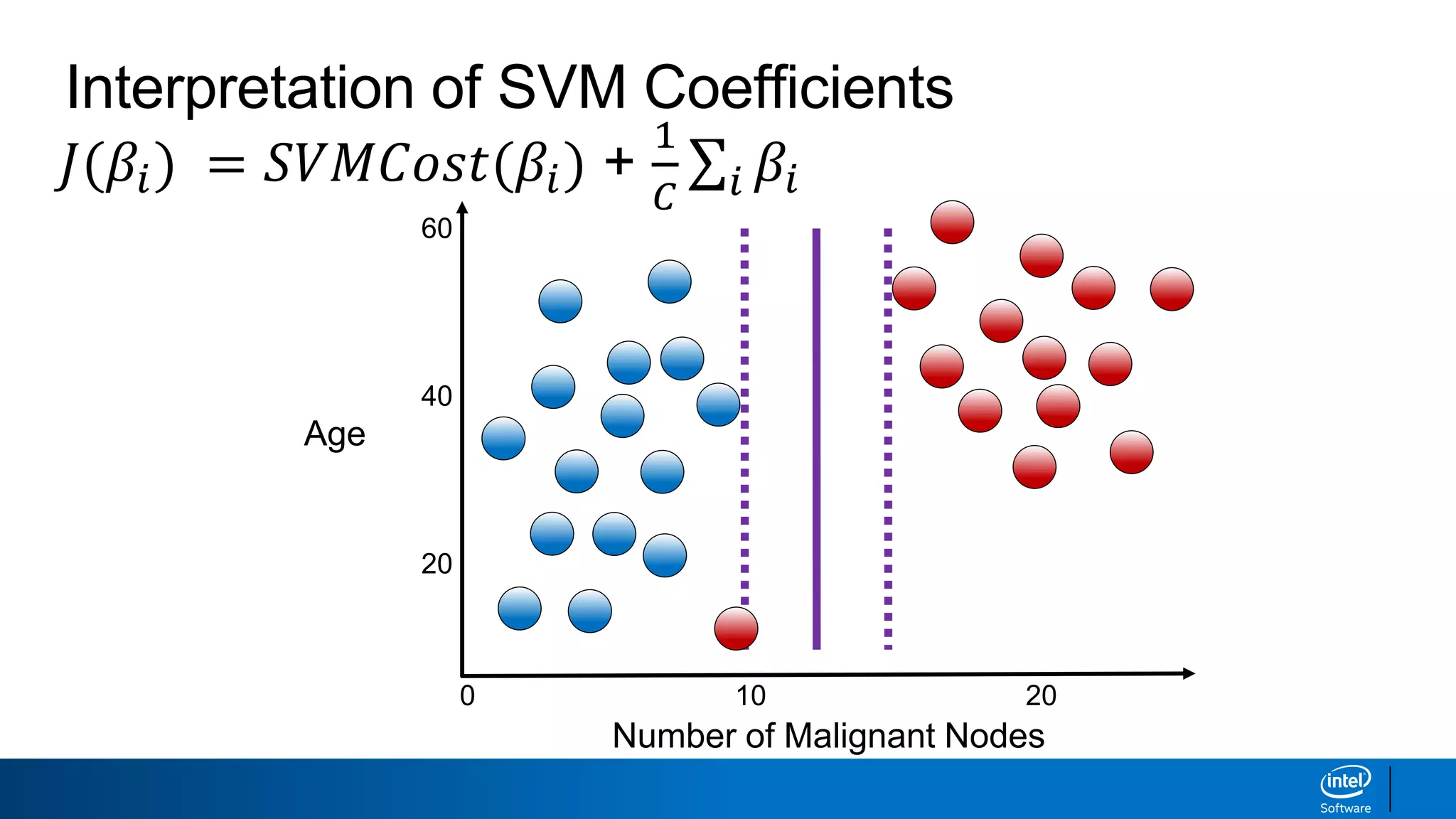
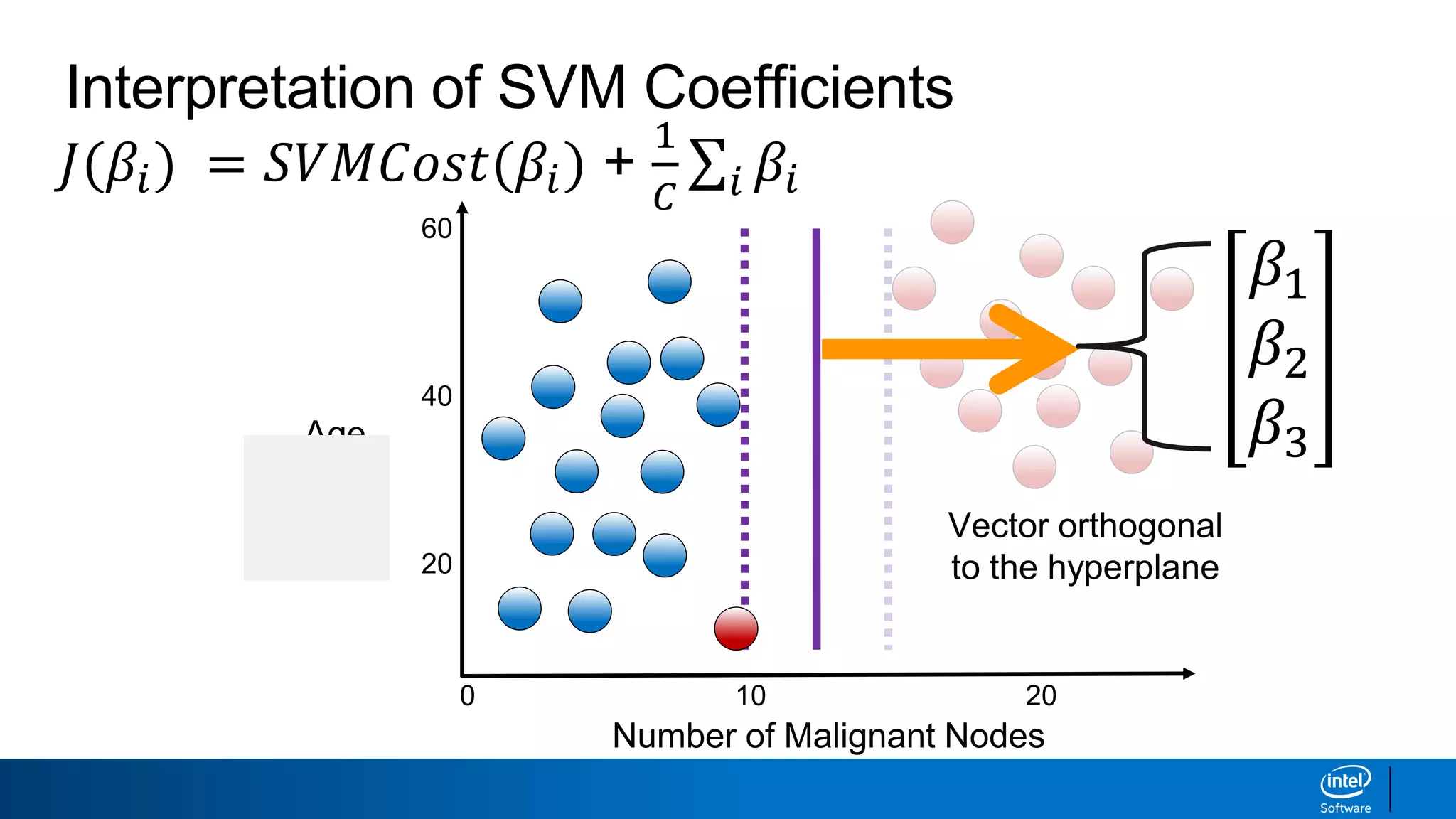
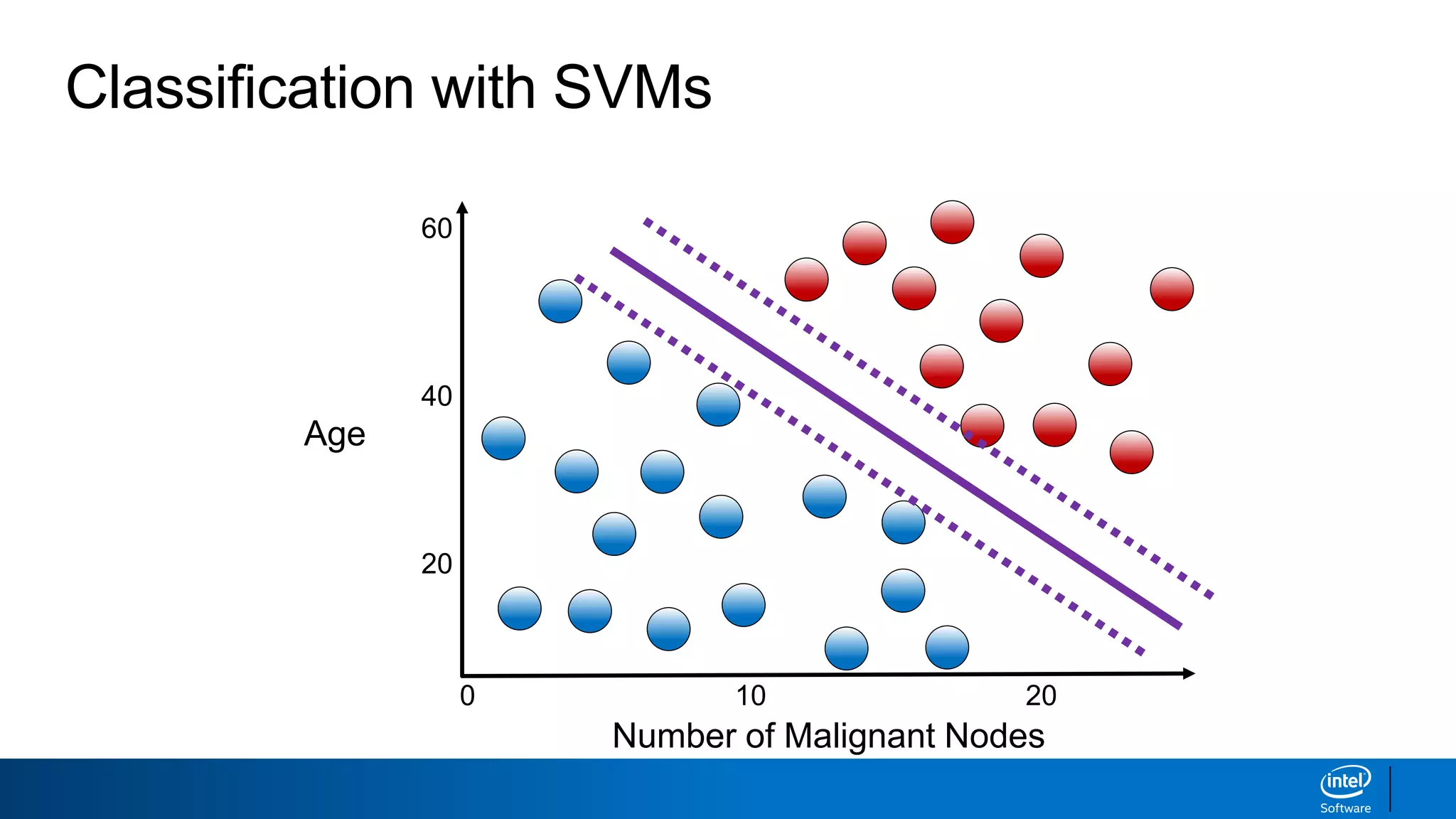
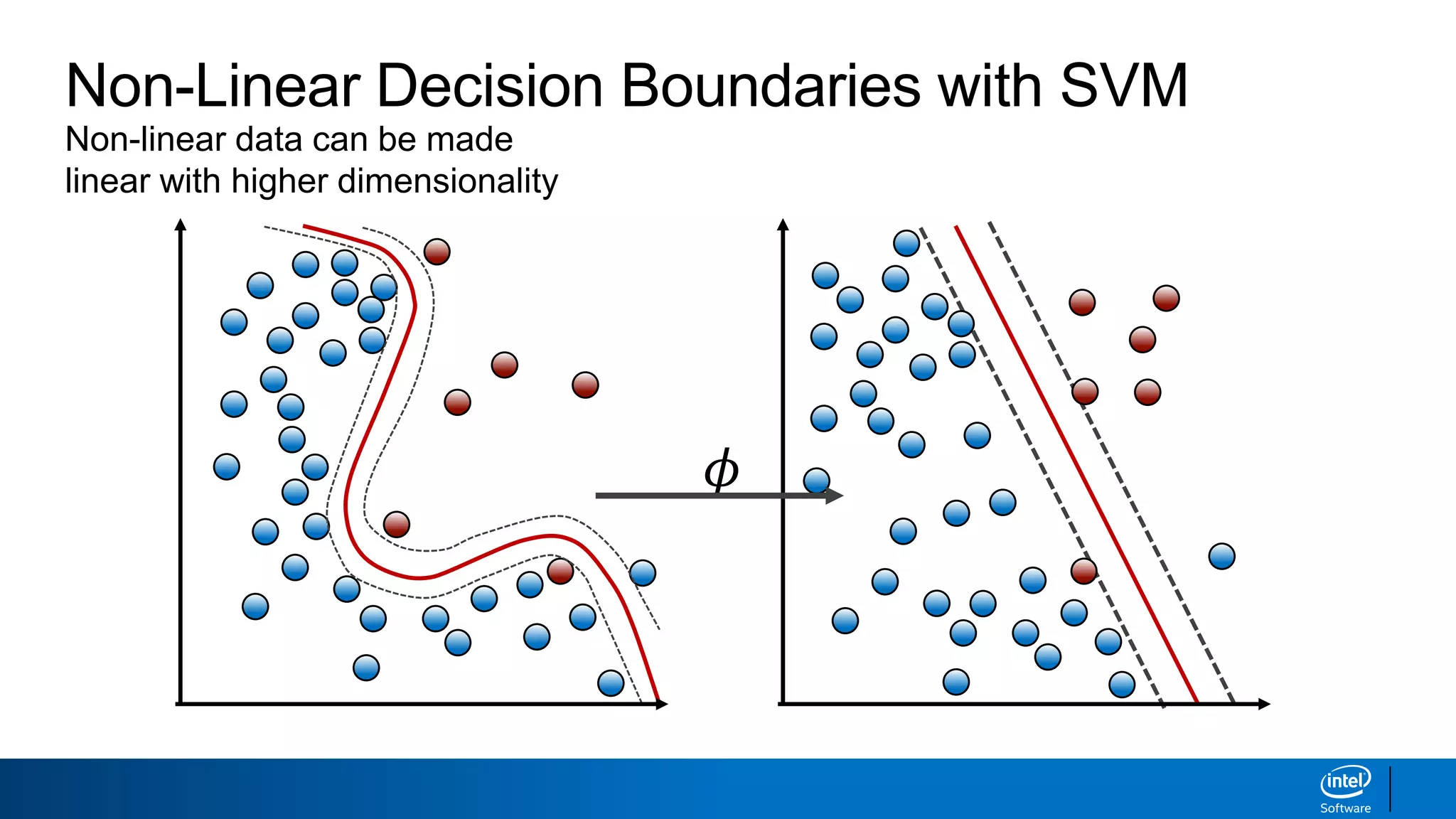
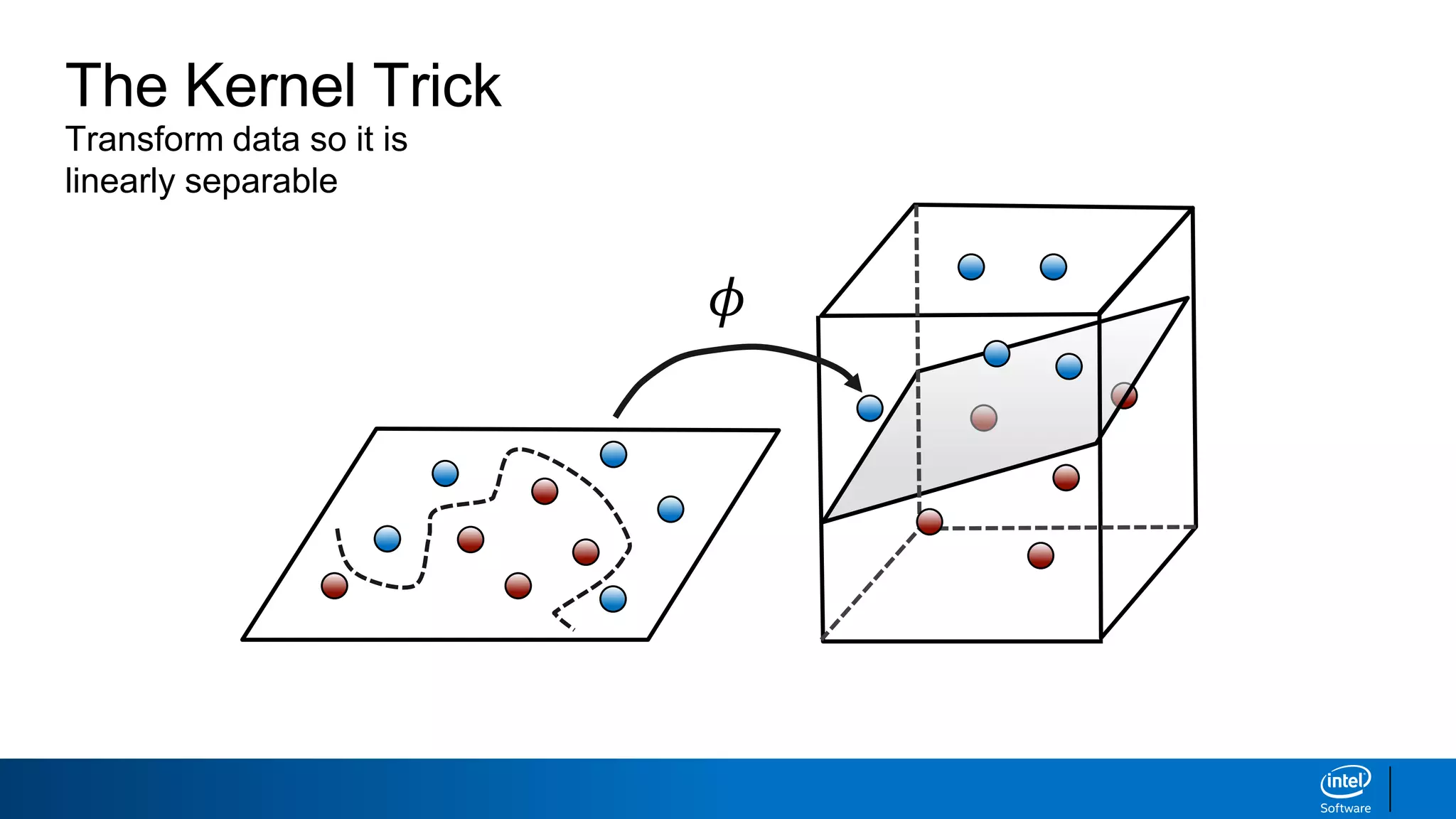
The document discusses support vector machines (SVMs). It explains that SVMs find the optimal separating hyperplane that maximizes the margin between two classes of data points. SVMs can handle both linear and non-linear classification problems by using kernels to implicitly map inputs into high-dimensional feature spaces. Common kernels include the radial basis function kernel, which transforms the data into an infinite dimensional space non-linearly.

1. Support Vector Machines

2. Legal Notices and Disclaimers
This presentation is for informational purposes only. INTEL MAKES NO WARRANTIES,
EXPRESS OR IMPLIED, IN THIS SUMMARY.
Intel technologies’ features and benefits depend on system configuration and may require
enabled hardware, software or service activation. Performance varies depending on system
configuration. Check with your system manufacturer or retailer or learn more at intel.com.
This sample source code is released under the Intel Sample Source Code License Agreement.
Intel and the Intel logo are trademarks of Intel Corporation in the U.S. and/or other countries.
*Other names and brands may be claimed as the property of others.
Copyright © 2017, Intel Corporation. All rights reserved.

3. Relationship to Logistic Regression
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
𝑦 𝛽 𝑥 =
1
1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε )

4. Support Vector Machines (SVM)
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5

5. Support Vector Machines (SVM)
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
Three
misclassifications

6. Support Vector Machines (SVM)
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
Two misclassifications

7. Support Vector Machines (SVM)
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
No misclassifications

8. Support Vector Machines (SVM)
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
No misclassifications—but is this the best position?

9. Support Vector Machines (SVM)
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
No misclassifications—but is this the best position?

10. Support Vector Machines (SVM)
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
Maximize the region between classes

11. Similarity Between Logistic Regression and SVM
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5

12. Number of Malignant Nodes
0
Age
60
40
20
10 20
Two features (nodes, age)
Two labels (survived, lost)
Classification with SVMs

13. Number of Malignant Nodes
0
Age
60
40
20
10 20
Find the line that best
separates classes
Classification with SVMs

14. Number of Malignant Nodes
0
Age
60
40
20
10 20
Find the line that best
separates classes
Classification with SVMs

15. Number of Malignant Nodes
0
Age
60
40
20
10 20
Find the line that best
separates classes
Classification with SVMs

16. Number of Malignant Nodes
0
Age
60
40
20
10 20
Find the line that best
separates classes
Classification with SVMs

17. Number of Malignant Nodes
0
Age
60
40
20
10 20
And include the largest
boundary possible
Classification with SVMs

18. Logistic Regression vs SVM Cost Functions
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5

19. Logistic Regression vs SVM Cost Functions
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
3
2
1
-3 -2 -1 0 1 2 3
Logistic Regression
Cost Function
for Lost Class

20. Logistic Regression vs SVM Cost Functions
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
3
2
1
-3 -2 -1 0 1 2 3
3
2
1
-3 -2 -1 0 1 2 3
Logistic Regression
Cost Function
for Lost Class
SVM
Cost Function
for Lost Class

21. The SVM Cost Function
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
3
2
1
-3 -2 -1 0 1 2 3
SVM
Cost Function
for Lost Class

22. The SVM Cost Function
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
3
2
1
-3 -2 -1 0 1 2 3
SVM
Cost Function
for Lost Class

23. The SVM Cost Function
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
3
2
1
-3 -2 -1 0 1 2 3
SVM
Cost Function
for Lost Class

24. The SVM Cost Function
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
3
2
1
-3 -2 -1 0 1 2 3
SVM
Cost Function
for Lost Class

25. The SVM Cost Function
Number of Positive Nodes
Survived: 0.0
Lost: 1.0Patient
Status
After Five
Years
0.5
3
2
1
-3 -2 -1 0 1 2 3
SVM
Cost Function
for Lost Class

26. Number of Malignant Nodes
0
Age
60
40
20
10 20
Outlier Sensitivity in SVMs

27. Number of Malignant Nodes
0
Age
60
40
20
10 20
Outlier Sensitivity in SVMs

28. Number of Malignant Nodes
0
Age
60
40
20
10 20
Outlier Sensitivity in SVMs

29. Number of Malignant Nodes
0
Age
60
40
20
10 20
Outlier Sensitivity in SVMs

30. Number of Malignant Nodes
0
Age
60
40
20
10 20
Outlier Sensitivity in SVMs
This is probably still the
correct boundary

31. Number of Malignant Nodes
0
Age
60
40
20
10 20
Regularization in SVMs
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖

32. Number of Malignant Nodes
0
Age
60
40
20
10 20
Regularization in SVMs
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖

33. Number of Malignant Nodes
0
Age
60
40
20
10 20
Regularization in SVMs
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖
Best Fit

34. Number of Malignant Nodes
0
Age
60
40
20
10 20
Regularization in SVMs
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖
Best Fit
Large

35. Number of Malignant Nodes
0
Age
60
40
20
10 20
Regularization in SVMs
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖

36. Number of Malignant Nodes
0
Age
60
40
20
10 20
Regularization in SVMs
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖
Slightly Higher

37. Number of Malignant Nodes
0
Age
60
40
20
10 20
Regularization in SVMs
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖
Slightly Higher
Much
Smaller

38. Interpretation of SVM Coefficients
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖
Number of Malignant Nodes
0
Age
60
40
20
10 20

39. Interpretation of SVM Coefficients
𝐽(𝛽𝑖) = 𝑆𝑉𝑀𝐶𝑜𝑠𝑡(𝛽𝑖) +
1
𝐶 𝑖 𝛽𝑖
Number of Malignant Nodes
0
Age
60
40
20
10 20
𝛽1
𝛽2
𝛽3
Vector orthogonal
to the hyperplane

40. Linear SVM: The Syntax
Import the class containing the classification method
from sklearn.svm import LinearSVC

41. Linear SVM: The Syntax
Import the class containing the classification method
from sklearn.svm import LinearSVC
Create an instance of the class
LinSVC = LinearSVC(penalty='l2', C=10.0)

42. Linear SVM: The Syntax
Import the class containing the classification method
from sklearn.svm import LinearSVC
Create an instance of the class
LinSVC = LinearSVC(penalty='l2', C=10.0)
regularization
parameters

43. Linear SVM: The Syntax
Import the class containing the classification method
from sklearn.svm import LinearSVC
Create an instance of the class
LinSVC = LinearSVC(penalty='l2', C=10.0)
Fit the instance on the data and then predict the expected value
LinSVC = LinSVC.fit(X_train, y_train)
y_predict = LinSVC.predict(X_test)

44. Linear SVM: The Syntax
Import the class containing the classification method
from sklearn.svm import LinearSVC
Create an instance of the class
LinSVC = LinearSVC(penalty='l2', C=10.0)
Fit the instance on the data and then predict the expected value
LinSVC = LinSVC.fit(X_train, y_train)
y_predict = LinSVC.predict(X_test)
Tune regularization parameters with cross-validation.

46. Kernels

47. Number of Malignant Nodes
0
Age
60
40
20
10 20
Classification with SVMs

48. Non-Linear Decision Boundaries with SVM
Non-linear data can be made
linear with higher dimensionality
𝜙

49. The Kernel Trick
Transform data so it is
linearly separable
𝜙

50. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget

51. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget
Approach 1:
Create higher order
features to
transform the data.
Budget2 +
Rating2 +
Budget * Rating +
…

52. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget
Approach 2:
Transform the
space to a different
coordinate system.

53. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget
Define Feature 1:
Similarity to
"Pulp Fiction"

54. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget
Define Feature 2:
Similarity to
"Black Swan"

55. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget
Define Feature 3:
Similarity to
"Transformers"

56. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget
Create a
Gaussian function
at feature 1
𝑎1(𝑥 𝑜𝑏𝑠) = 𝑒𝑥𝑝
− (𝑥𝑖
𝑜𝑏𝑠
− 𝑥𝑖
𝑃𝑢𝑙𝑝 𝐹𝑖𝑐𝑡𝑖𝑜𝑛
)2
2𝜎2

57. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget
Create a
Gaussian function
at feature 2
𝑎1(𝑥 𝑜𝑏𝑠) = 𝑒𝑥𝑝
− (𝑥𝑖
𝑜𝑏𝑠
− 𝑥𝑖
𝐵𝑙𝑎𝑐𝑘 𝑆𝑤𝑎𝑛
)2
2𝜎2

58. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget Create a
Gaussian function
at feature 3
𝑎1(𝑥 𝑜𝑏𝑠) = 𝑒𝑥𝑝
− (𝑥𝑖
𝑜𝑏𝑠
− 𝑥𝑖
𝑇𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑒𝑟𝑠
)2
2𝜎2

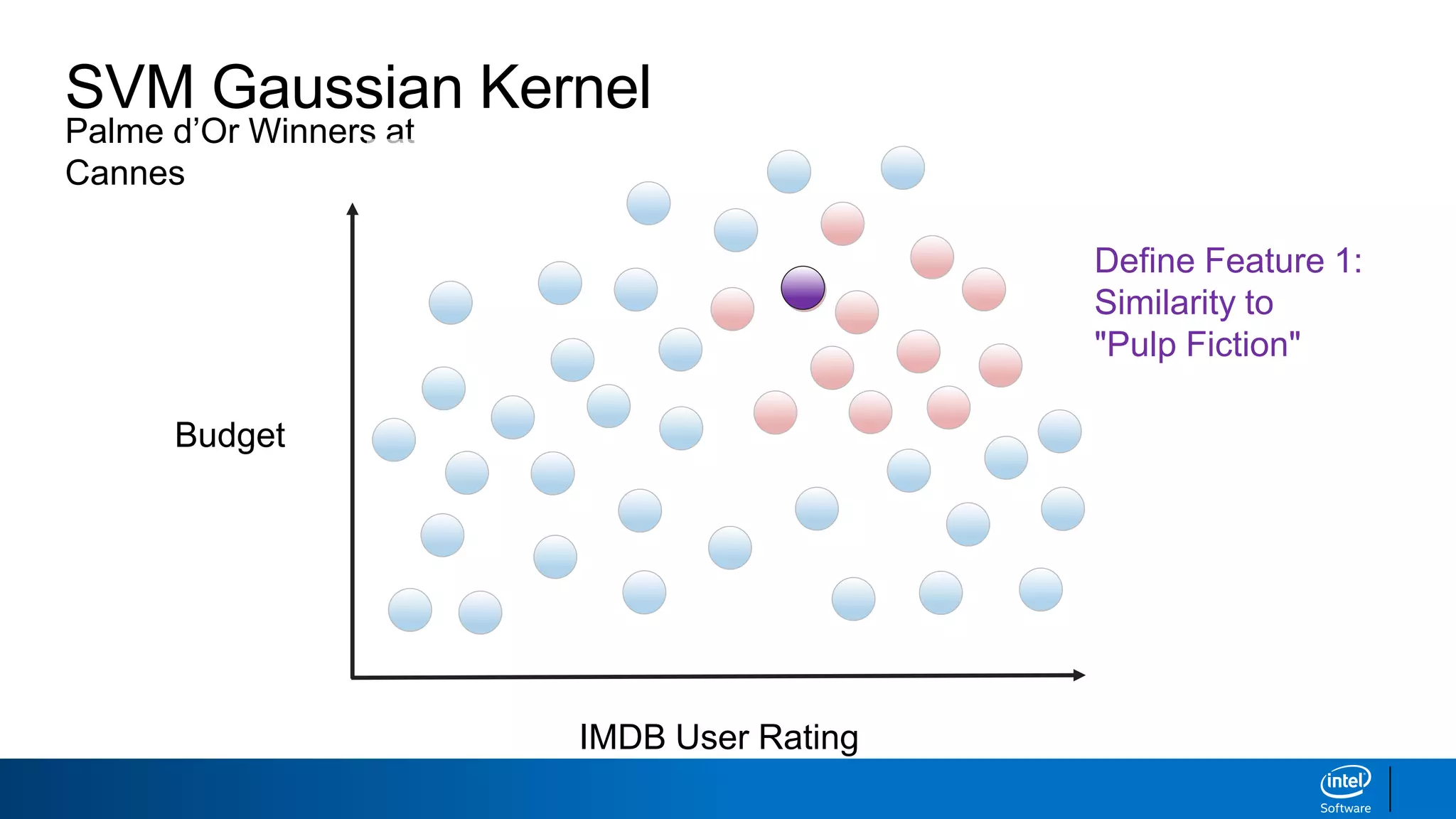
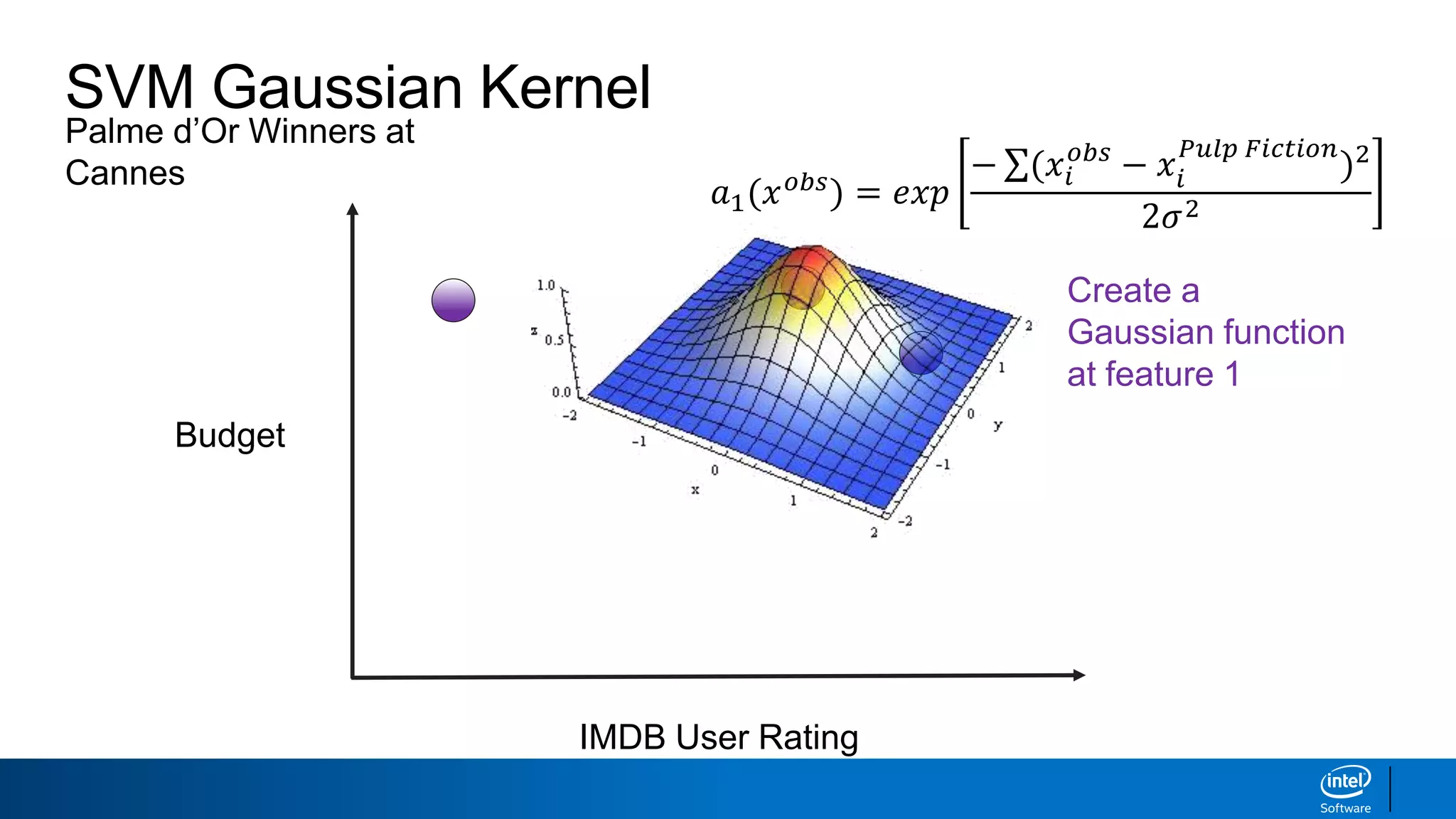
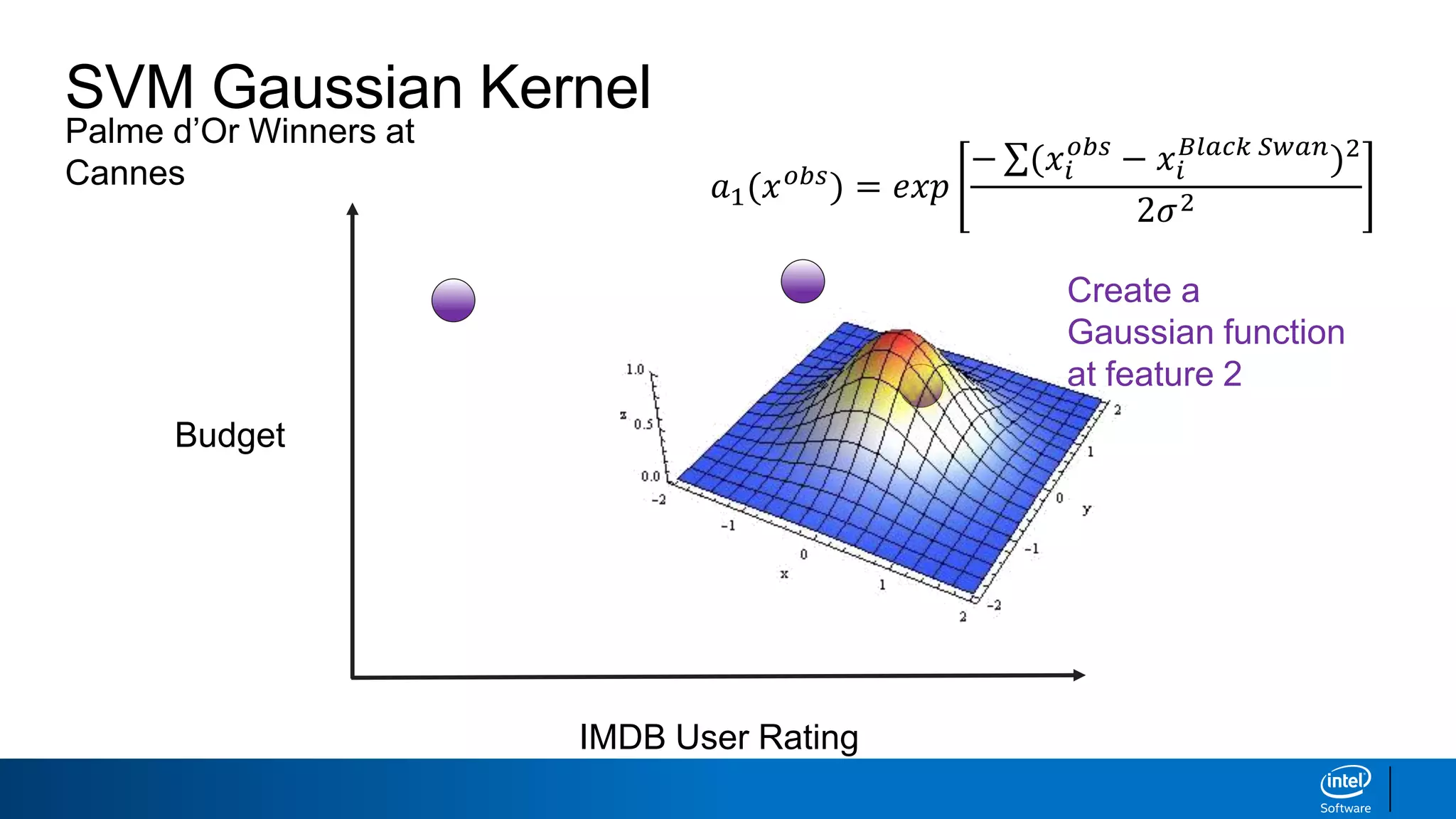
59. SVM Gaussian Kernel
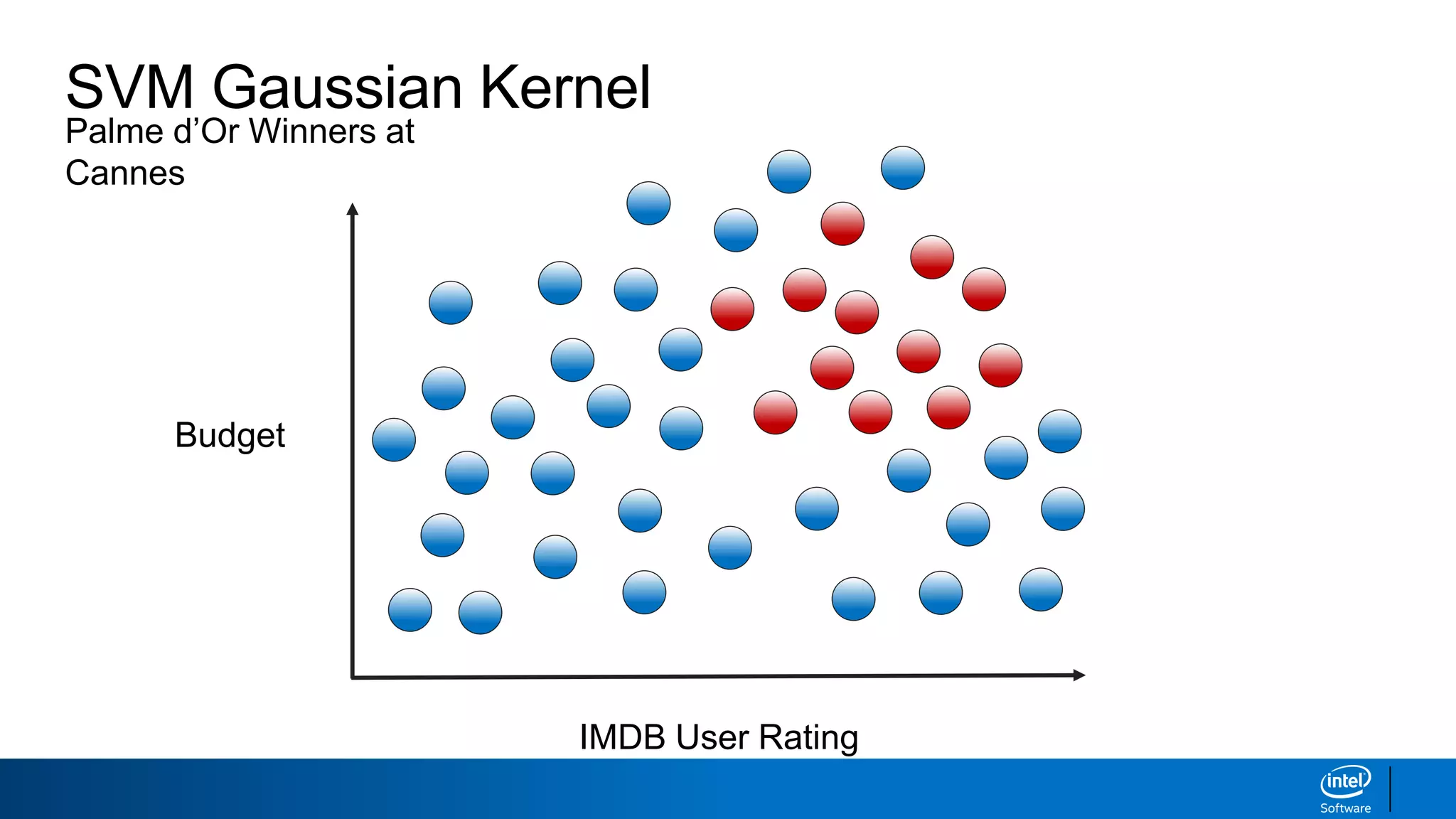
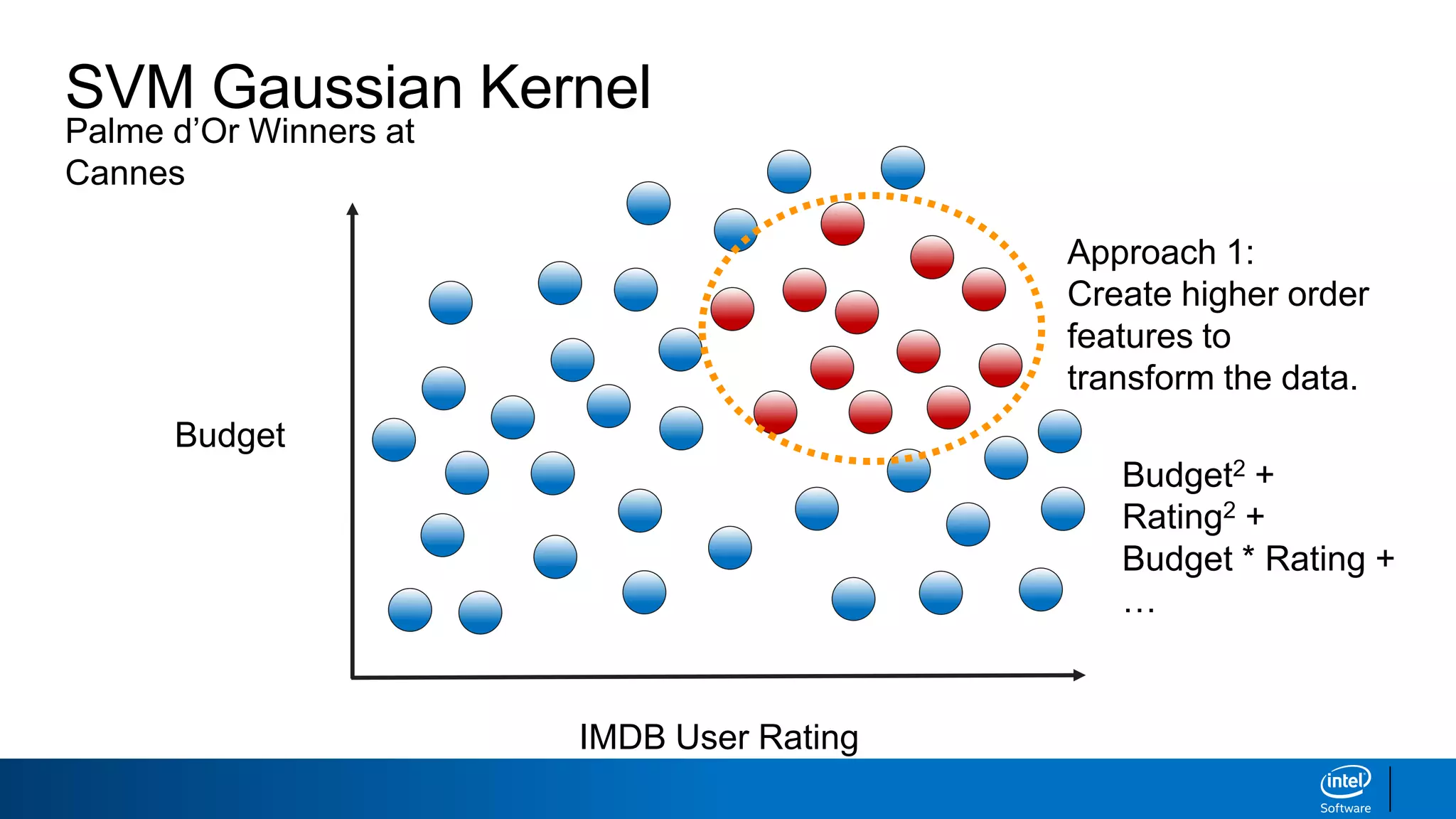
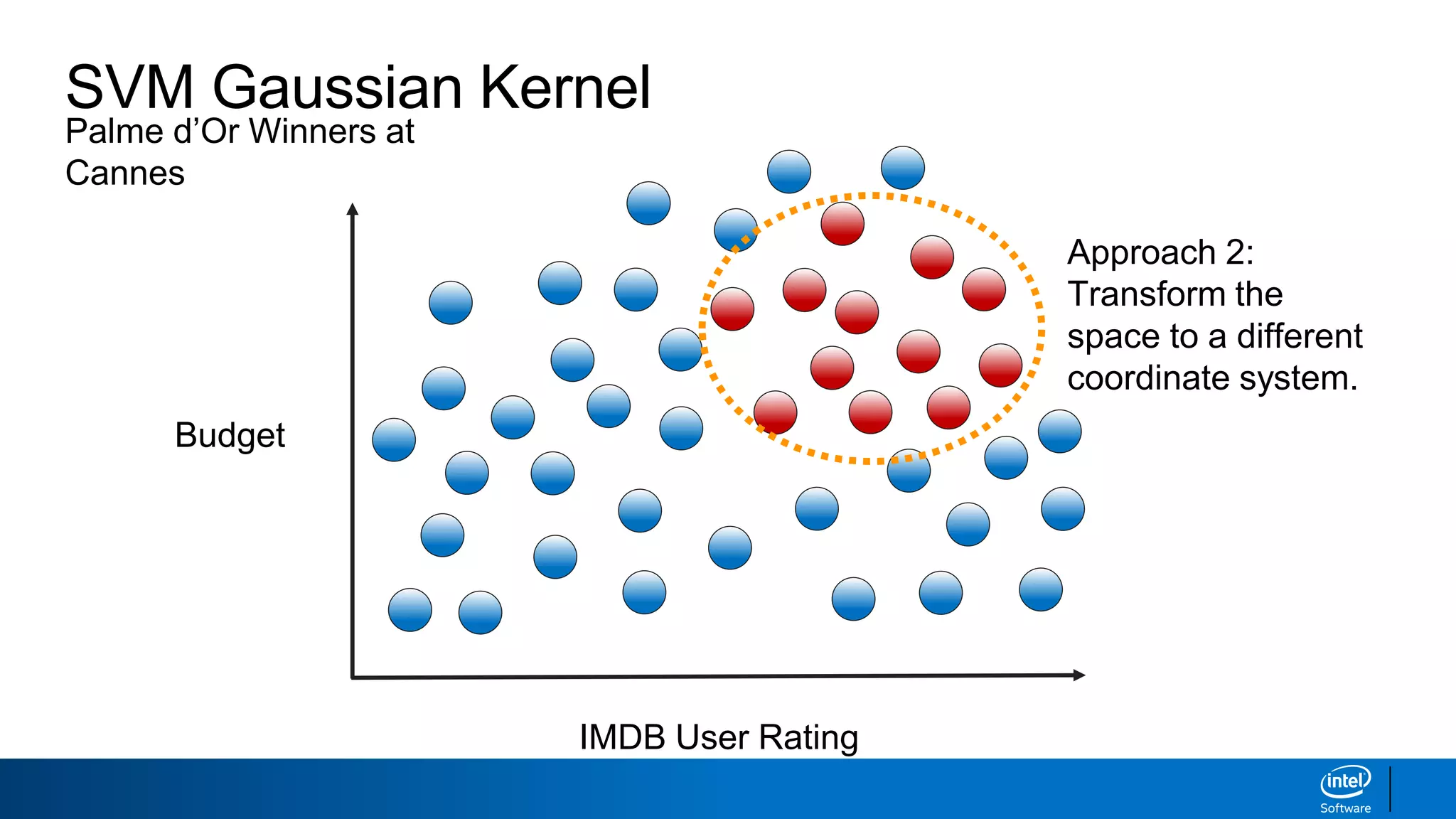
IMDB User Rating
Budget
Transformation:
[x1, x2]  [0.7a1 , 0.9a2 , -0.6a3]

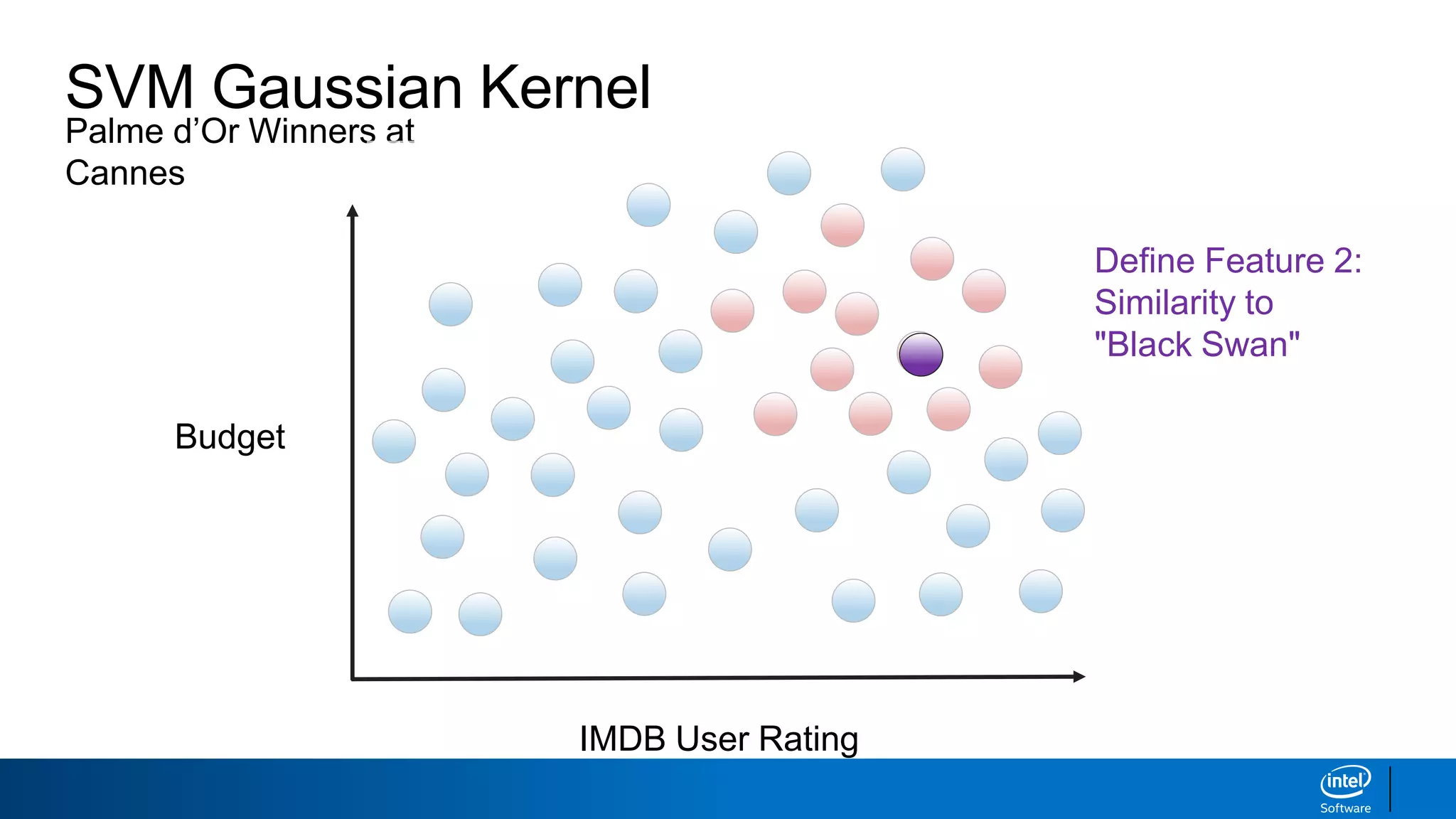
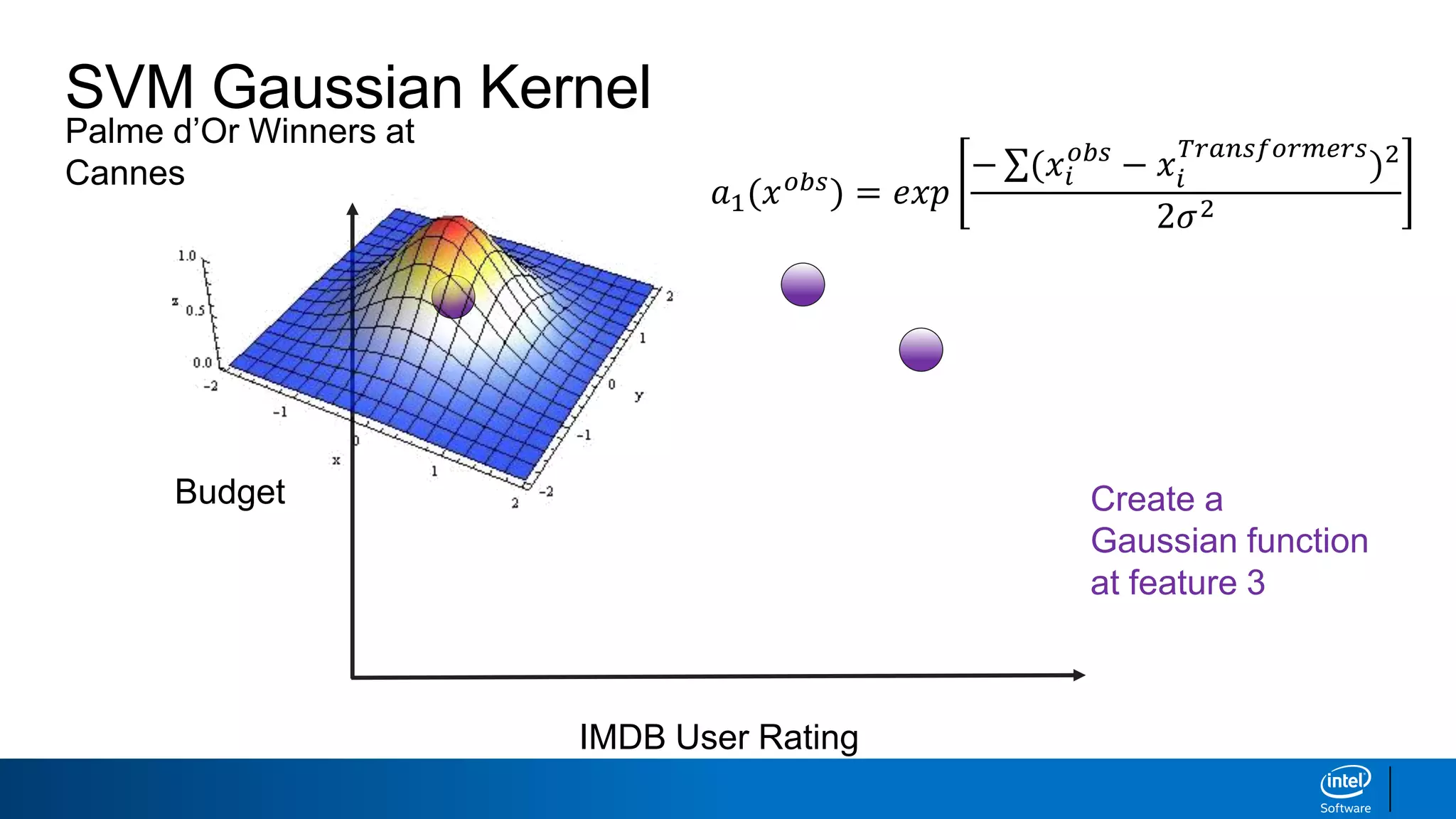
60. SVM Gaussian Kernel
IMDB User Rating
Budget
a1=0.90
a2=0.92
a3=0.30
Transformation:
[x1, x2]  [0.7a1 , 0.9a2 , -0.6a3]
a3
a2
a1

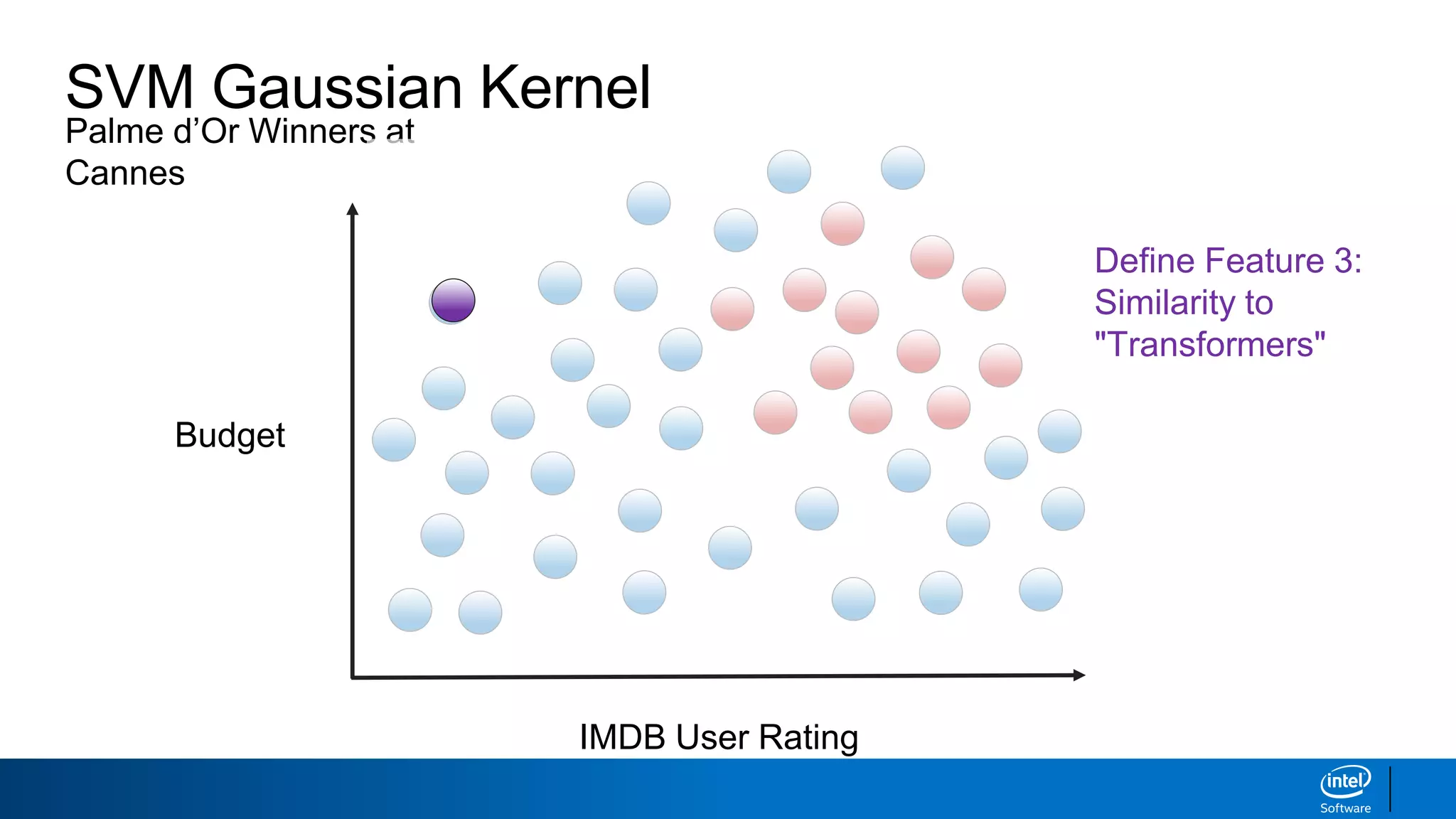
61. SVM Gaussian Kernel
IMDB User Rating
Budget
a1=0.50
a2=0.60
a3=0.70 Transformation:
[x1, x2]  [0.7a1 , 0.9a2 , -0.6a3]
a3
a1
a2

62. SVM Gaussian Kernel
x2 (IMDB Rating)
x1(Budget)
a1 (Pulp Fiction)
a3 (Transformers)
a2 (Black Swan)
Transformation:
[x1, x2]  [0.7a1 , 0.9a2 , -0.6a3]

63. Classification in the New Space
a1 (Pulp Fiction)
a3 (Transformers)
a2 (Black Swan)
Transformation:
[x1, x2]  [0.7a1 , 0.9a2 , -0.6a3]

64. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget

65. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget

66. Palme d’Or Winners at
Cannes
SVM Gaussian Kernel
IMDB User Rating
Budget
Radial Basis Function
(RBF) Kernel

67. Import the class containing the classification method
from sklearn.svm import SVC
SVMs with Kernels: The Syntax

68. Import the class containing the classification method
from sklearn.svm import SVC
Create an instance of the class
rbfSVC = SVC(kernel='rbf', gamma=1.0, C=10.0)
SVMs with Kernels: The Syntax

69. Import the class containing the classification method
from sklearn.svm import SVC
Create an instance of the class
rbfSVC = SVC(kernel='rbf', gamma=1.0, C=10.0)
Fit the instance on the data and then predict the expected value
rbfSVC = rbfSVC.fit(X_train, y_train)
y_predict = rbfSVC.predict(X_test)
Tune kernel and associated parameters with cross-validation.
SVMs with Kernels: The Syntax
set kernel and
associated
coefficient
(gamma)

70. Import the class containing the classification method
from sklearn.svm import SVC
Create an instance of the class
rbfSVC = SVC(kernel='rbf', gamma=1.0, C=10.0)
Fit the instance on the data and then predict the expected value
rbfSVC = rbfSVC.fit(X_train, y_train)
y_predict = rbfSVC.predict(X_test)
Tune kernel and associated parameters with cross-validation.
SVMs with Kernels: The Syntax
"C" is penalty
associated with
the error term

71. Import the class containing the classification method
from sklearn.svm import SVC
Create an instance of the class
rbfSVC = SVC(kernel='rbf', gamma=1.0, C=10.0)
Fit the instance on the data and then predict the expected value
rbfSVC = rbfSVC.fit(X_train, y_train)
y_predict = rbfSVC.predict(X_test)
Tune kernel and associated parameters with cross-validation.
SVMs with Kernels: The Syntax

72. SVMs with Kernels: The Syntax
Import the class containing the classification method
from sklearn.svm import SVC
Create an instance of the class
rbfSVC = SVC(kernel='rbf', gamma=1.0, C=10.0)
Fit the instance on the data and then predict the expected value
rbfSVC = rbfSVC.fit(X_train, y_train)
y_predict = rbfSVC.predict(X_test)
Tune kernel and associated parameters with cross-validation.

73. Feature Overload
SVMs with RBF Kernels are very slow to
train with lots of features or data
Problem
Solution
Construct approximate kernel map with
SGD using Nystroem or RBF sampler

74. Feature Overload
SVMs with RBF Kernels are very slow to
train with lots of features or data
Problem
Solution
Construct approximate kernel map with
SGD using Nystroem or RBF sampler

75. Feature Overload
SVMs with RBF Kernels are very slow to
train with lots of features or data
Problem
Solution
Construct approximate kernel map with
SGD using Nystroem or RBF sampler.
Fit a linear classifier.

76. Faster Kernel Transformations: The Syntax
Import the class containing the classification method
from sklearn.kernel_approximation import Nystroem
Create an instance of the class
nystroemSVC = Nystroem(kernel='rbf', gamma=1.0,
n_components=100)
Fit the instance on the data and transform
X_train = nystroemSVC.fit_transform(X_train)
X_test = nystroemSVC.transform(X_test)
Tune kernel parameters and components with cross-validation.

77. Faster Kernel Transformations: The Syntax
Import the class containing the classification method
from sklearn.kernel_approximation import Nystroem
Create an instance of the class
nystroemSVC = Nystroem(kernel='rbf', gamma=1.0,
n_components=100)
Fit the instance on the data and transform
X_train = nystroemSVC.fit_transform(X_train)
X_test = nystroemSVC.transform(X_test)
Tune kernel parameters and components with cross-validation.
multiple non-
linear kernels
can be used

78. Faster Kernel Transformations: The Syntax
Import the class containing the classification method
from sklearn.kernel_approximation import Nystroem
Create an instance of the class
nystroemSVC = Nystroem(kernel='rbf', gamma=1.0,
n_components=100)
Fit the instance on the data and transform
X_train = nystroemSVC.fit_transform(X_train)
X_test = nystroemSVC.transform(X_test)
Tune kernel parameters and components with cross-validation.
kernel and
gamma are
identical to SVC

79. Faster Kernel Transformations: The Syntax
Import the class containing the classification method
from sklearn.kernel_approximation import Nystroem
Create an instance of the class
nystroemSVC = Nystroem(kernel='rbf', gamma=1.0,
n_components=100)
Fit the instance on the data and transform
X_train = nystroemSVC.fit_transform(X_train)
X_test = nystroemSVC.transform(X_test)
Tune kernel parameters and components with cross-validation.
n_components
is number of
samples

80. Faster Kernel Transformations: The Syntax
Import the class containing the classification method
from sklearn.kernel_approximation import RBFsampler
Create an instance of the class
rbfSample = RBFsampler(gamma=1.0,
n_components=100)
Fit the instance on the data and transform
X_train = rbfSample.fit_transform(X_train)
X_test = rbfSample.transform(X_test)
Tune kernel parameters and components with cross-validation.

81. Faster Kernel Transformations: The Syntax
Import the class containing the classification method
from sklearn.kernel_approximation import RBFsampler
Create an instance of the class
rbfSample = RBFsampler(gamma=1.0,
n_components=100)
Fit the instance on the data and transform
X_train = rbfSample.fit_transform(X_train)
X_test = rbfSample.transform(X_test)
Tune kernel parameters and components with cross-validation.
RBF is only
kernel that can
be used

82. Faster Kernel Transformations: The Syntax
Import the class containing the classification method
from sklearn.kernel_approximation import RBFsampler
Create an instance of the class
rbfSample = RBFsampler(gamma=1.0,
n_components=100)
Fit the instance on the data and transform
X_train = rbfSample.fit_transform(X_train)
X_test = rbfSample.transform(X_test)
Tune kernel parameters and components with cross-validation.
parameter
names are
identical to
previous

83. When to Use Logistic Regression vs SVC
Features Data Model Choice
Many (~10K
Features)
Few (<100 Features)
Few (<100 Features)
Small (1K rows)
Medium (~10k rows)
Many (>100K Points)
Simple, Logistic or LinearSVC
SVC with RBF
Add features, Logistic, LinearSVC
or Kernel Approx.