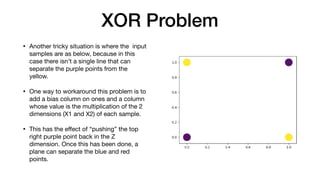
The document discusses logistic regression as a supervised learning algorithm for binary classification, including its predictive model based on input features and the sigmoid function. It also highlights challenges such as overfitting and methods for regularization, specifically L1 (lasso) and L2 (ridge) techniques. Additionally, it addresses complex classification scenarios, illustrated by the donut and XOR problems, and proposes solutions to handle them effectively.

1. Machine Learning
Logistic Regression

2. Agenda
• Logistic Regression
• Generalisation, Over-fitting & Regularisation
• Donut Problem
• XOR Problem

3. What is Logistic Regression?
• Learning
• A supervised algorithm that learns to separate training samples into two categories.
• Each training sample has one or more input values and a single target value of
either 0 or 1.
• The algorithm learns the line, plane or hyper-plane that best divides the training
samples with targets of 0 from those with targets of 1.
• Prediction
• Uses the learned line, plane or hyper-plane to predict the whether an input sample
results in a target of 0 or 1.

4. Logistic Regression

5. Logistic Regression
• Each training sample has an x made
up of multiple input values and a
corresponding t with a single value.
• The inputs can be represented as an
X matrix in which each row is sample
and each column is a dimension.
• The outputs can be represented as T
matrix in which each row is a sample
has has a value of either 0 or 1.

6. Logistic Regression
• Our predicated T values are
calculated by multiplying out X
values by a weight vector and
applying the sigmoid function to the
result.

7. Logistic Regression
• The sigmoid function is:
• And has a graph like this:
• By applying this function we end up
with predictions that are between
zero and one

8. Logistic Regression
• We use an error function know as
the cross-entropy error function:
• Where t is the actual target value (0
or 1) and t circumflex is the
predicted target value for a sample.
• If the actual target is 0 the left hand
term is 0, leaving the red line:
• If the actual target is 1, the right
hand term is 0, leaving the blue line:

9. Logistic Regression
• We use the chain rule to partially
differentiate E with respect to wi to find
the gradient to use for this weight in
gradient descent:
• Where:

10. Logistic Regression
• Taking the first term:
• Taking the third term:

11. Logistic Regression
• Taking the second term:

12. Logistic Regression
• Multiplying the three
derivatives and simplifying
ends up with:
• In matrix form, for all weights:
• In code we use this with
gradient descent to derive the
weights that minimise the
error.

13. Logistic Regression

14. Logistic Regression

15. Generalisation, Over-fitting &
Regularisation

16. Generalisation & Over-fitting
• As we train our model with more and more data the it may start to fit the training data more and
more accurately, but become worse at handling test data that we feed to it later.
• This is know as “over-fitting” and results in an increased generalisation error.
• To minimise the generalisation error we should
• Collect as much sample data as possible.
• Use a random subset of our sample data for training.
• Use the remaining sample data to test how well our model copes with data it was not trained
with.
• Also, experiment with adding higher degrees of polynomials (X2, X3, etc) as this can reduce
overfitting.

17. L1 Regularisation (Lasso)
• In L1 regularisation we add a penalty to
the error function:
• Expanding this we get:
• Take the derivative with respect to w to
find our gradient:
• Where sign(w) is -1 if w < 0, 0 if w = 0
and +1 if w > 0
• Note that because sign(w) has no
inverse function we cannot solve for w
and so must use gradient descent.

18. L1 Regularisation (Lasso)

19. L2 Regularisation (Ridge)
• In L2 regularisation we the sum of
the squares of the weights to the
error function.
• Expanding this we get:
• Take the derivative with respect to
w to find our gradient:

20. L2 Regularisation (Ridge)

21. Donut Problem

22. Donut Problem
• Sometimes data will be distributed like
this
• In this cases it would appear that logistic
regression cannot be used to classify the
red and blue points because there is no
single line that separates them.
• However, one way to workaround this
problem is to add a bias column of ones
and a column whose value is the distance
of each sample from the centre of these
circles.

23. XOR Problem

24. XOR Problem
• Another tricky situation is where the input
samples are as below, because in this
case there isn’t a single line that can
separate the purple points from the
yellow.
• One way to workaround this problem is to
add a bias column on ones and a column
whose value is the multiplication of the 2
dimensions (X1 and X2) of each sample.
• This has the effect of “pushing” the top
right purple point back in the Z
dimension. Once this has been done, a
plane can separate the blue and red
points.

25. Summary
• Logistic Regression
• Generalisation, Over-fitting & Regularisation
• Donut Problem
• XOR Problem