Downloaded 10 times
Uploaded byrohith attaluri
Soft computing
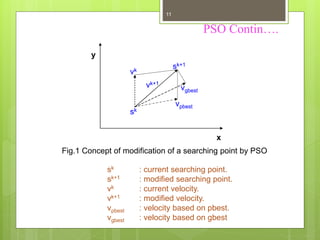
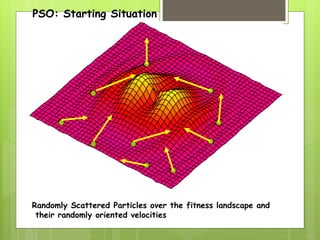
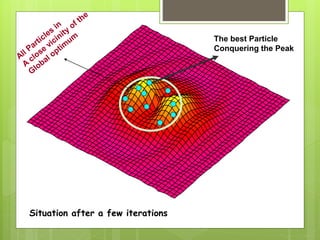
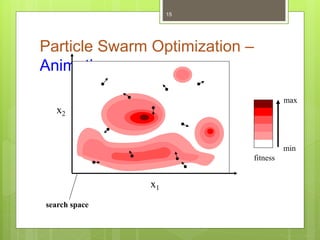
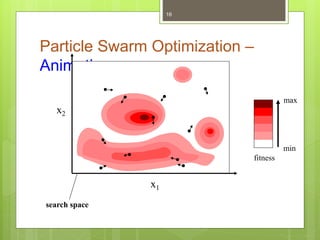
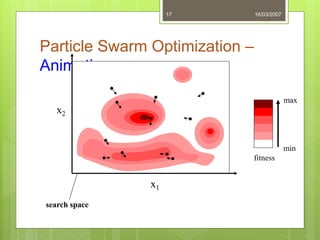
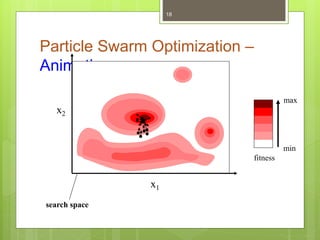
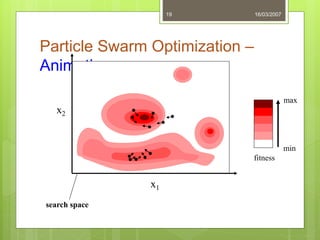
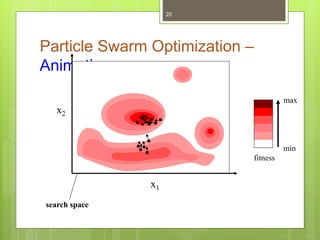
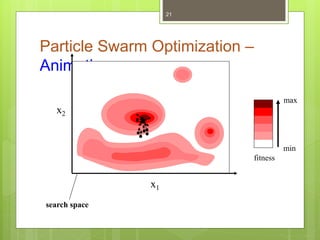
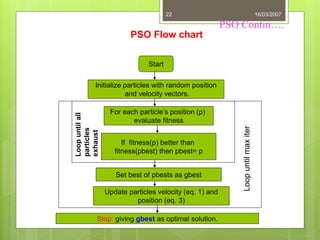
Particle Swarm Optimization (PSO) is a stochastic optimization technique inspired by social behavior observed in swarms of animals, utilizing individual and group bests to guide particle movement in a solution space. Each particle in the PSO algorithm updates its position based on its own best known position and the best known position of its neighbors, driven by random acceleration factors. The process continues iteratively until a stopping criterion is met, determining the optimal solution.
Soft computing
- 1. SOFT COMPUTING PARTICLE SWAMOPTIMIZATION(PSO)
- 2. Most recent multi-agentstochastic parallel search techniques is: Particle Swarm Optimization (PSO; Eberhart & Kennedy, IEEE Evocomp, 1995)
- 3. Inventors (1995) Russell EberhartJames Kennedy (electrical engineer) (social-psychologist) 16/03/20073
- 5.
- 6. Particle Swarm Optimization (PSO) PSO is a robust stochastic optimization technique based on the movement and intelligence of swarms. PSO applies the concept of social interaction to problem solving. 6
- 7. Why do animalsswarm? Defense against predators Enhanced predator detection Minimizing chance of capture Enhanced foraging success Better chances to find a mate Decrease of energy consumption 7
- 8. Social Insects Several millionyears Efficient Flexible Robust Solve many Problems: Find food, feed Build a nest … 8
- 9. Social Insects Several millionyears Efficient Flexible Robust Solve many Problems: Find food, feed Build a nest … 9
- 10. • Each particlekeeps track of its coordinates in the solution space which are associated with the best solution (fitness) that has achieved so far by that particle. This value is called personal best , pbest. • Another best value that is tracked by the PSO is the best value obtained so far by any particle in the neighborhood of that particle. This value is called gbest. • The basic concept of PSO lies in accelerating each particle toward its pbest and the gbest locations, with a random weighted accelaration at each time step as shown in Fig.1 PSO Contin…. 16/03/200710
- 11. Fig.1 Concept ofmodification of a searching point by PSO sk : current searching point. sk+1 : modified searching point. vk : current velocity. vk+1 : modified velocity. vpbest : velocity based on pbest. vgbest : velocity based on gbest PSO Contin…. 11 x y sk vk vpbest vgbest sk+1 vk+1 sk vk vpbest vgbest sk+1 vk+1
- 12. PSO Contin…. 12 • Eachparticle tries to modify its position using the following information: the current positions, the current velocities, the distance between the current position and pbest, the distance between the current position and the gbest. • The modification of the particle’s position can be mathematically modeled according the following equation : Vi k+1 = wVi k +c1 rand1(…) x (pbesti-si k) + c2 rand2(…) x (gbest-si k) ….. (1) where, vi k : velocity of agent i at iteration k, w: weighting function, cj : weighting factor, rand : uniformly distributed random number between 0 and 1, si k : current position of agent i at iteration k, pbesti : pbest of agent i, gbest: gbest of the group.
- 13. PSO: Starting Situation RandomlyScattered Particles over the fitness landscape and their randomly oriented velocities
- 14. The best Particle Conqueringthe Peak Situation after a few iterations
- 15. Particle Swarm Optimization– Animation 15 x1 x2 fitness min max search space
- 16. Particle Swarm Optimization– Animation 16 x1 x2 search space fitness min max
- 17. Particle Swarm Optimization– Animation 16/03/200717 x1 x2 fitness min max search space
- 18. Particle Swarm Optimization– Animation 18 x1 x2 fitness min max search space
- 19. Particle Swarm Optimization– Animation 16/03/200719 x1 x2 fitness min max search space
- 20. Particle Swarm Optimization– Animation 20 x1 x2 fitness min max search space
- 21. Particle Swarm Optimization– Animation 21 x1 x2 fitness min max search space
- 22. PSO Contin…. 16/03/200722 PSO Flowchart Start Initialize particles with random position and velocity vectors. For each particle’s position (p) evaluate fitness If fitness(p) better than fitness(pbest) then pbest= p Loopuntilall particles exhaust Set best of pbests as gbest Update particles velocity (eq. 1) and position (eq. 3) Loopuntilmaxiter Stop: giving gbest as optimal solution.
- 23. To know more THEsite: Particle Swarm Central, http://www.particleswarm.net Clerc M., Kennedy J., "The Particle Swarm-Explosion, Stability, and Convergence in a Multidimensional Complex Space", IEEE Transaction on Evolutionary Computation, 2002,vol. 6, p. 58-73.