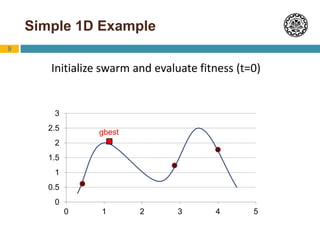
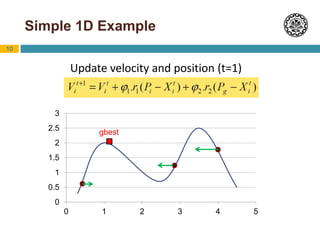
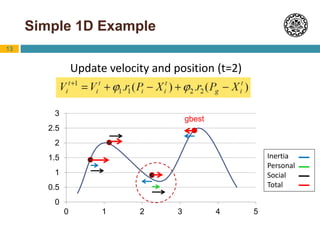
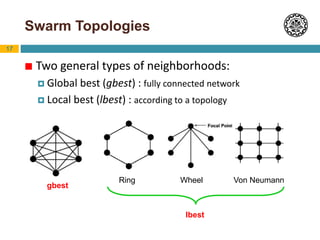
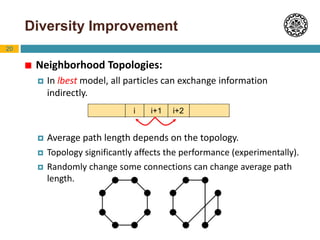
Particle Swarm Optimization (PSO) is an optimization technique inspired by swarm behavior in animals. It works by having a population (swarm) of potential solutions (particles) and updating the movement of the particles based on their personal best position and the global best position. The basic algorithm initializes a swarm of random particles and then iteratively updates the velocity and position of particles using equations that factor in inertia, cognition toward personal best, and social behavior toward global best. PSO has been shown to perform comparably to genetic algorithms but requires fewer parameters to adjust. Variants and hybridizations of PSO have also been developed to improve performance for different problem types.

1. Particle Swarm Optimization
(PSO)
Mansour Nejati

2. 2
Introduction : Swarm Intelligence
 Study of collective behavior in decentralized, self-
organized systems.
 Originated from the study of colonies, or swarms of
social organisms.
 Collective intelligence arises from interactions.

3. 3
Introduction
 Particle Swarm Optimization:
 Introduced by Kennedy & Eberhart 1995
 Inspired by social behavior of birds and shoals of fish
 Swarm intelligence-based optimization
 Nondeterministic
 Population-based optimization
 Performance comparable to Genetic algorithms

4. 4
Particle Swarm Optimization
 Swarm : a set of particles (S)
 Particle: a potential solution
 Position,
 Velocity ,
 Each particle maintains
 Individual best position:
 Swarm maintains its global best:

5. 5
PSO Algorithm
 Basic algorithm of PSO:
1. Initialize the swarm from the solution space
2. Evaluate fitness of each particle
3. Update individual and global bests
4. Update velocity and position of each particle
5. Go to step 2, and repeat until termination condition

6. 6
PSO Algorithm (cont.)
 Original velocity update equation:
 with
 : acceleration constant
Inertia Cognitive Component Social Component

7. 7
PSO Algorithm (cont.)
 Original velocity update equation:
 with
 : acceleration constant
 Position Update:
Inertia Cognitive Component Social Component

8. 8
PSO Algorithm - Parameters
 Acceleration constant
 Small values limit the movement of the particles
 Large values : tendency to explode toward infinity
 In general
 Maximum velocity
 Velocity is a stochastic variable => uncontrolled trajectory

9. 9
Simple 1D Example
0
0.5
1
1.5
2
2.5
3
0 1 2 3 4 5
Initialize swarm and evaluate fitness (t=0)
gbest

10. 10
Simple 1D Example
0
0.5
1
1.5
2
2.5
3
0 1 2 3 4 5
Update velocity and position (t=1)
gbest

11. 11
Simple 1D Example
0
0.5
1
1.5
2
2.5
3
0 1 2 3 4 5
Evaluate fitness
Update personal and global best (t=2)
gbest

12. 12
Simple 1D Example
0
0.5
1
1.5
2
2.5
3
0 1 2 3 4 5
Evaluate fitness
Update personal and global best (t=2)
gbest

13. 13
Simple 1D Example
0
0.5
1
1.5
2
2.5
3
0 1 2 3 4 5
gbest
Update velocity and position (t=2)
Inertia
Personal
Social
Total

14. 14
Rate of Convergence Improvement
 Inertia weight:
 Scaling the previous velocity
 Control search behavior
 High values  exploration
 Low values  exploitation

15. 15
PSO with Inertia weight
 can be decreased over time:
 Linear [0.9 to 0.4]
 Nonlinear
 main disadvantage:
 once the inertia weight is decreased, the swarm loses
its ability to search new areas (can not recover its
exploration mode).

16. 16
Rate of Convergence Improvement
 Constriction Factor:
 Canonical PSO
 Typically ,
 Can converge without using Vmax (velocity clamping)
 Improve the convergence by damping the oscillations

17. 17
Swarm Topologies
 Two general types of neighborhoods:
 Global best (gbest) : fully connected network
 Local best (lbest) : according to a topology
gbest
Ring Wheel Von Neumann
lbest

18. 18
Lbest vs. Gbest
 Gbest converges fast but may be trapped in a local optima.
 Lbest is slower in convergence but has more chances to find
an optimal solution.
 Most efficient neighborhood structure, in general,
 Fully Informed PSO (FIPS):
 Each individual is influenced by successes of all its neighbors.

19. 19
Diversity Improvement
 Based on lbest model.
 Usually slow down the convergence rate.
 Spatial Neighborhoods:
 Partition particles based on spatial location.
 Calculate the largest distance between any two particles.
 Select neighboring particles according to ratio:
 Selection threshold can be varied over time.
 Start with small ratio (lbest) and gradually increase the ratio.

20. 20
Diversity Improvement
 Neighborhood Topologies:
 In lbest model, all particles can exchange information
indirectly.
 Average path length depends on the topology.
 Topology significantly affects the performance (experimentally).
 Randomly change some connections can change average path
length.
i i+1 i+2

21. 21
Diversity Improvement
 Subpopulations:
 Previously used in GA.
 Original swarm is partitioned to subpopulations.
 PSO is applied to each subpopulation.
 An interaction scheme is used for information sharing
between subpopulations.
 Each subpopulation can search the smaller region of
search space.

22. 22
Discrete PSO
 Binary PSO:
 Introduces by kennedy and Eberhart.
 Each individual (particle) has to take a binary decision.
 Predisposition is derived based on individual and group
performance:
Previous state predisposition

23. 23
Binary PSO (cont.)
 determines a threshold in the probability function and
therefore should be bounded in the range of [0.0, 1.0].
 state of the dth position in the string at time t:
 Where is a random number with a uniform distribution.
Vid
1

24. 24
PSO Variants
 Hybrid PSO
 Incorporate the capabilities of other evolutionary
computation techniques.
 Adaptive PSO
 Adaptation of PSO parameters for a better performance.
 PSO in complex environments
 Multiobjective or constrained optimization problems or tracking
dynamic systems.
 Other variants
 variations to the original formulation to improve its performance.

25. 25
Hybrid PSO
 GA-PSO:
 combines the advantages of swarm intelligence and a
natural selection mechanism.
 jump from one area to another by the selection
mechanism  accelerating the convergence speed.
 capability of “breeding”.
 replacing agent positions with low fitness values, with
those with high fitness, according to a selection rate

26. 26
Hybrid PSO
 EPSO:
 Evolutionary PSO
 Incorporates a selection procedure
 Self-adapting of parameters
 The particle movement is defined as:

27. 27
Hybrid PSO : EPSO
 Mutation of weights and global best:
 Learning parameters can be either fixed or
dynamically changing as strategic parameters.
 Survival Selection:
 Stochastic tournament.

28. 28
Hybrid PSO : EPSO

29. 29
Hybrid PSO : DEPSO
 Hybrid of Differential Evolution and PSO.
 A DE operator applied to the particle’s best position to
eliminate the particles falling into local minima.
 Alternation:
 Original PSO algorithm at the odd iterations.
 DE operator at the even iterations.

30. 30
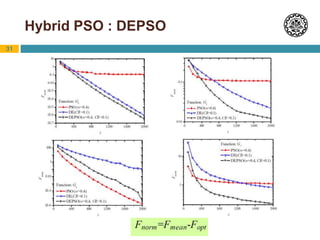
Hybrid PSO : DEPSO
 DE mutation on particle’s best positions:
 where k is a random integer value within [1,n] which
ensures the mutation in at least one dimension.
Trial point:
For each dth dimention:

31. 31
Hybrid PSO : DEPSO

32. 32
Dynamic Tracking in PSO
 The classical PSO is very effective in solving static
optimization problems but is not as efficient when
applied to a dynamic system in which the optimal value
may change repeatedly.
 An adaptive approach has been introduced for this
problem:
 Detection of environmental changes:
 changed-gbest-value
 fixed-gbest-values
 rerandomizing a certain number of particles

33. 33
Applications
 Convenience of realization, properties of low constraint on
the continuity of objective function and joint of search space,
and ability of adapting to dynamic environment, make PSO be
applied in more and more fields.
 Some PSO applications:
 Electronics and electromagnetic
 Signal, Image and video processing
 Neural networks
 Communication networks
 …

34. 34
Thanks for your attention