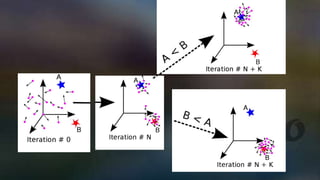
This document discusses particle swarm optimization (PSO), which is an optimization technique inspired by swarm intelligence and the social behavior of bird flocking or fish schooling. PSO uses a population of candidate solutions called particles that fly through the problem hyperspace, with each particle adjusting its position based on its own experience and the experience of neighboring particles. The algorithm iteratively improves the particles' positions to locate the best solution based on fitness evaluations.

2. 12024119-085
12024119-138
12024119-087

3. Find values of the variables that minimize or maximize the objective
function while satisfying the constraints.
Goal Of Optimization

4. We can Find the optimization level in any problem by:
• Providing Many Solutions of one problem
• Compute the complexity of all of them.
• Compare Every Solution’s complexities with others.
• See what is the best option with completing the constraints.

5. There are three major types of Optimization Techniques
1. Calculas Based Techniques: All numeric Based Problems are included in this technique.
2. Enumerative Techniques: involve evaluating each and every point of the finite,
or discretized infinite, search space in order to arrive at the optimal solution, Dynamic
Programming is the best example of Enumerative Techniques.
3. Random Techniques: Random Techniques are same as Enumerative Techniques but add
some additional functionality like go to the solution space in random position like
Genetic Algorithm Random choice is used as a tool to guide a highly explorative search
through a coding of the parameter space. The guided random search methods are
useful in problems where the search space is huge and complex. Particle Swarm
Optimization is the part of the Random Techniques.

6. Particle Swarm optimization based on Swarm Intelligence.
Swarm Intelligence
• SI is Artificial Intelligence, based on the collective behavior of decentralized, self organized
Systems.
• The expression was introduced by Garardo Beni and Jing Wang in 1989, in the context of celluar
robotic systems.
• Si systems are typically made up of a population of simple agents interacting locally with on
another and with their environment.
• Natural examples of SI include and colonies, bird flocking, animal herding , bacterial growth
and fish schooling.

7. • U.S. military is investigating swarm techniques for controlling unmanned vehicles, like Drones
• NASA is investigating the use of swarm technology for planetary mapping.

8. • The PSO algorithm was first described in 1995 by James Kennedy and Russell C. Eberhart
inspired by social behavior of bird flocking or fish schooling.
“PSO is an artificial intelligence (AI) technique that can be used to find approximate solutions
to extremely difficult or impossible numeric maximization and minimization problems.”
• Hypotheses are plotted in this space and seeded with an initial velocity,
as well as a communication channel between the particles.
• Simple algorithm, easy to implement and few parameters to adjust mainly the velocity.

9. How it work
• PSO is initialized with a group of random particles (solutions) and then searches for
optimal by updating generations.
• Particles move through the solution space, and are evaluated according to some fitness
criterion after each time step. In every iteration, each particle is updated by following
two "best" values.

10. How it work
Searches Hyperspace of Problem for Optimum
n Define problem to search
p How many dimensions?
p Solution criteria?
n Initialize Population
p Random initial positions
p Random initial velocities
n Determine Global Best Position
n Determine Personal Best Position
n Update Velocity and Position Equations

11. Best Options In PS0
• The first one is the best solution (fitness) it has achieved so far (the fitness value is also stored).
This value is called pbest.
Another "best" value that is tracked by the particle swarm optimizer is the best value obtained
so far by any particle in the population. This second best value is a global best and called gbest.

12. Each particle tries to modify its current position and velocity according to the distance between its
current position and pbest, and the distance between its current position and gbest.
Current Position[n+1] = Current Position [n] + v[n+1]
current position[n+1]: position of particle at n+1th
iteration
current position[n]: position of particle at nth iteration
v[n+1]: particle velocity at n+1th iteration
vn+1: Velocity of particle at n+1 th iteration
Vn : Velocity of particle at nth iteration
c1 : acceleration factor related to gbest
c2 : acceleration factor related to lbest
rand1( ): random number between 0 and 1
rand2( ): random number between 0 and 1
gbest: gbest position of swarm
pbest: pbest position of particle
21( )*( CurrentPosition ) 2( )*( CurrentPositionn n1 1 best,n best,n )randv v c rand p c gnn     

13. For each particle
Initialize particle with feasible random number
End
Do
For each particle
Calculate the fitness value
If the fitness value is better than the best fitness value
(pbest) in history
Set current value as the new pbest
End
Choose the particle with the best fitness value of all the
particles as the gbest
For each particle
Calculate particle velocity according to velocity update
equation
Update particle position according to position update
equation
End
While maximum iterations or minimum error criteria
is not attained

15. The process of PSO algorithm in finding optimal values follows the work of an animal
society which has no leader.
Particle swarm optimization consists of a swarm of particles, where particle represent a
potential solution (better condition).
Particle will move through a multidimensional search space to find the best position in
that space (the best position may possible to the maximum or minimum values).
Summary

16. p PSOt – A Matlab Toolbox
p Function Optimization
p Neural Net Training
Application

17. PSOt – A Mat lab Toolbox
Matlab: Scientific computing language run
in interpreter mode on a wide variety of
operating systems.
Toolbox: Suite of Matlab ‘plug-in’
programs developed by third parties.