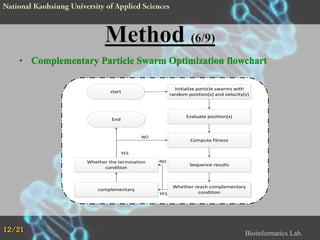
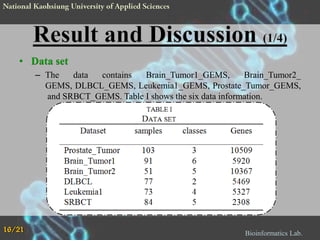
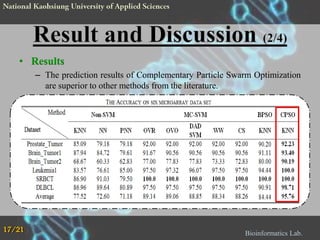
The document proposes a Complementary Particle Swarm Optimization (CPSO) method for feature selection in DNA microarray data. CPSO was designed to overcome limitations of standard PSO getting trapped in local optima. CPSO uses a complementary strategy to move particles to new search regions. It was tested on six microarray datasets and achieved lower classification errors than other methods. Future work will combine CPSO with K-Nearest Neighbors classification to potentially further improve performance.

1. Reporter: Hua-Fang Chang
Bioinformatics Lab.

2.  Introduction
 Method
 Result and Discussion
 Conclusion
2/21
Bioinformatics Lab.

3. • DNA microarrayWeight
Height
Age
Interest
65
Basketball
– DNA microarray could contribute the biological scholars to
analyze the various disease types; it 23 widely used to identify
was
166
50
Soccer
the DNA types, cells, and cancer classification.
156
54
– DNA microarray data was usually huge and complexity.
189
90
22
Soccer
177
68
24
Soccer
– Feature selection technique was applied to select the helpful
DNA dimension.
165
54
63
Basketball
– Feature selection to choose the subset from the dataset, and used
156
45
50
tennis
the classification to estimate the subset.
3/21
Bioinformatics Lab.

4. • Algorithm
– Many computational algorithms have been proposed to DNA
microarray.
› Genetic Algorithm (GA), 1975
Each candidate solution has a set of properties (its chromosomes or
genotype) which can be mutated and altered.
› Particle Swarm Optimization(PSO), 1995
Particle swarm optimization (PSO) is a population based stochastic
optimization technique developed by Dr. Eberhart and Dr. Kennedy in
1995, inspired by social behavior of bird flocking or fish schooling.
› Binary particle swarm optimization (BPSO), 2005
In their model a particle will decide on "yes" or " no", "true" or "false",
"include" or "not to include" etc. also this binary values can be a
representation of a real value in binary search space.
4/21
Bioinformatics Lab.

5. › Complementary Particle Swarm Optimization :
The complementary strategy aims to assist the particle search ability
which help the particle deviating in a local optimum by moving their
position to a new region in the search space.
› K-Nearest Neighbor :
The K-Nearest Neighbor (KNN) method is used to classify the features.
› leave-one-out cross-validation :
leave-one-out cross-validation (LOOCV) to compute classification error
rates.
5/21
Bioinformatics Lab.

6. – We propose a Complementary Particle Swarm Optimization for DNA
microarray.
– In standard PSO, particles may get trapped in a local optimum due
to the premature convergence of particles.
– Therefore, we used the complementary strategy to avoid the
particles trapped in a local optimum by moving the new region in
the search space.
6/21
Bioinformatics Lab.

7. • Complementary Particle Swarm Optimization (CPSO)
– PSO has been developed through simulation of the social behavior of
organisms, such as the social behavior observed of birds in a flock or fish in a
school.
– Each particle is affected by its past experience and the swarm behavior.
– PSO has been successfully applied in many research areas, produced results
more efficiently and has a lower cost compared to other methods.
– However, PSO is not suitable for optimization problems in a discrete feature
space.
– We propose a Complementary Particle Swarm Optimization(CPSO) to
overcome this problem.
7/21
Bioinformatics Lab.

8. • Complementary
– The complementary strategy aims to assist the particle search ability
which help the particle deviating in a local optimum by moving their
position to a new region in the search space.
– We used the complementary function to generate the new particles, and
replace the 50% of the particles in the swarm.
8/21
Bioinformatics Lab.

9. • Initialization
–
–
–
–
9/21
Randomly initialize particle swarm(particle = 50).
Adjust position of particle swarm
Evaluate fitness of particle swarm
number of iterations=100
Bioinformatics Lab.

10. • Particle update
– In CPSO, each particle is updated according to the following equations:
old
v new w vid
id
new
xid
old
xid
c1 r1
pbestid
old
xid
c2 r2
gbestd
old
xid
new
vid
• where w is the inertia weight that controls the impact of the previous velocity of a
particle.
• c1 and c2 are acceleration constants that control the distance a particle moves at each
generation.
• r1 and r2 are two random numbers between [0, 1].
old
new
• v id and v id represent the velocity of the new and old particles, respectively.
• Particles x old and x new denote the position of the current particle and the updated
id
id
particle, respectively.
10/21
Bioinformatics Lab.

11. wLDW
( wm ax wm in )
Iterationm ax Iterationm in
Iterationm ax
wm in
• Position
and were the current position (solution) and the updated particle
position. We use the LDW strategy to update the inertia weight w.
• The wmax and wmin were the value 0.9 and 0.4, respectively. Iterationmax and
Iterationi were the maximal number of iterations and the current number of
iterations, respectively. The function made the inertia weight w was linearly
decreases from 0.9 to 0.4 though iteration.
11/21
Bioinformatics Lab.

12. • Complementary Particle Swarm Optimization flowchart
Initialize particle swarms with
random position(x) and velocity(v)
start
Evaluate position(x)
End
NO
Compute fitness
YES
Whether the termination
condition
complementary
12/21
NO
YES
Sequence results
Whether reach complementary
condition
Bioinformatics Lab.

13. • K-Nearest Neighbor (K-NN)
– Each data points can according to its own features in a D-dimensional space.
K-NN classification effect the subject for the number of impact of these K
neighbors.
– We used the Euclidean distance to compute all the testing data distance nearest
the K know type data to decided the testing data type.
• Leave-one-out cross-validation (LOOCV)
– In the LOOCV procedure, N samples are divide into a testing data and the N-1
training samples.
13/21
Bioinformatics Lab.

14.  PSO
particle
Consider the gbest and pbesti
pbesti
gbest
14/21
Bioinformatics Lab.

15.  CPSO
(9,10)
particle
pbesti
gbest
Coordinate Axis
(6,5)
Convert binary
Complementary
15/21
(0110,0101)
(1001,1010)
Bioinformatics Lab.

16. • Data set
– The
data
contains
Brain_Tumor1_GEMS,
Brain_Tumor2_
GEMS, DLBCL_GEMS, Leukemia1_GEMS, Prostate_Tumor_GEMS,
and SRBCT_GEMS. Table I shows the six data information.
16/21
Bioinformatics Lab.

17. • Results
– The prediction results of Complementary Particle Swarm Optimization
are superior to other methods from the literature.
17/21
Bioinformatics Lab.

18. • Discussion
– In the pretreatment process, the feature selection can effectively reduce
the calculation time without negatively affecting classification accuracy.
– Feature selection uses relatively fewer features since only selective
features need to be used. This does not affect the classification accuracy
in a negative way.
– We perform an ‘and’ logic operation for all bits of all pbest values.
pbest is the previously optimal position of each particle. In CPSO, if
the position of pbest in each particle is recorded as {1}, then the new
bit of a complementary will be {1} as well after the ‘and’ logic
operation is performed, else it is {0}.
18/21
Bioinformatics Lab.

19. – The purpose of this study was to improve on standard PSO.
– Some classification algorithms, such as decision tree, K-nearest
neighbor aim at all feature to evaluate the classification performance.
– Experiments show that K-NN often achieve higher classification
accuracy than other classification method. In a future work, we will
combine K-NN with CPSO to evaluate and compare their classification
accuracy and performances.
19/21
Bioinformatics Lab.

20. • The classification error rate obtained by the CPSO method that is the
lowest classification error rate when compare with other several methods in
six DNA microarray datasets.
• The results on the DNA microarray dataset show that the complementary
particle swarm optimization is superior to Non-SVM, MC-SVM, and
BPSO in terms of diversity, convergence and computation cost.
• In the future, we intend to use different properties and other algorithms for
DNA microarray in order to further enhance feature selection efficacy.
20/21
Bioinformatics Lab.

21. E-mail: mjasd5@gmail.com
21/21
Bioinformatics Lab.