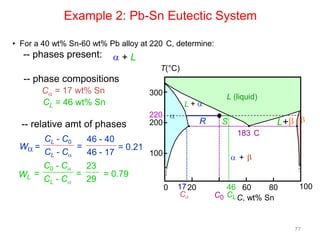
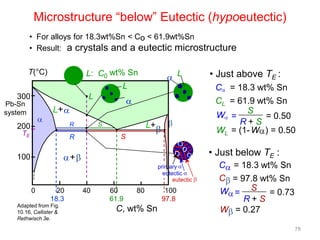
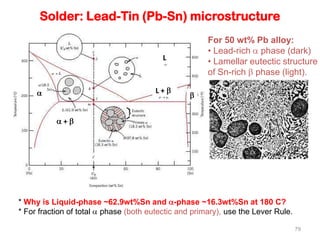
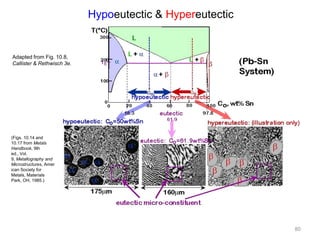
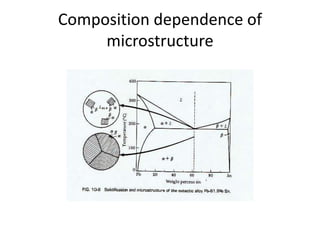
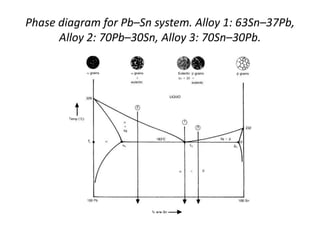
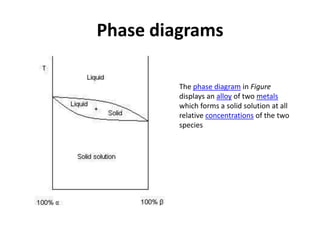
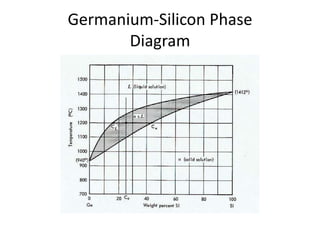
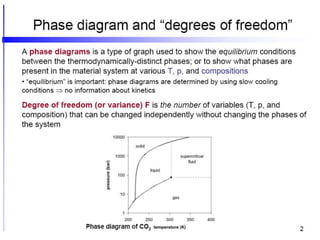
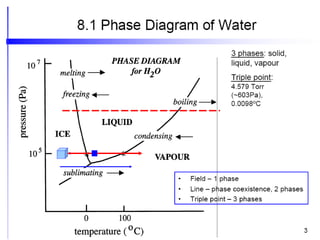
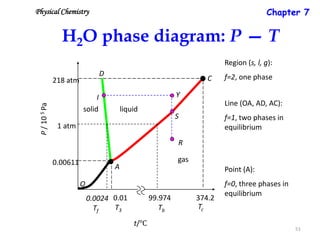
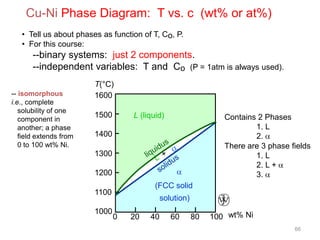
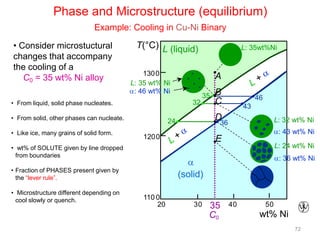
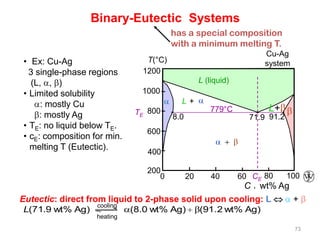
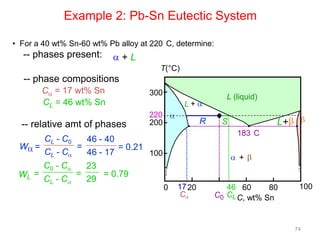
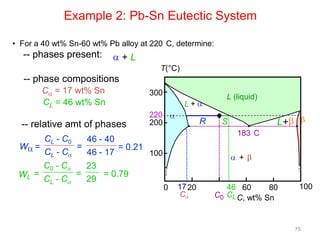
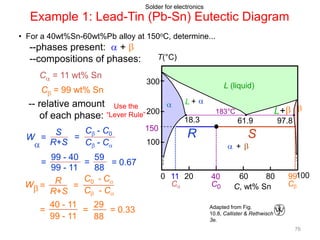
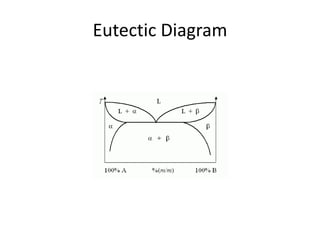
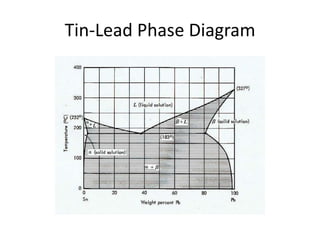
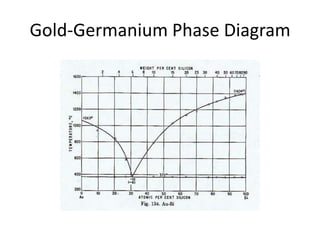
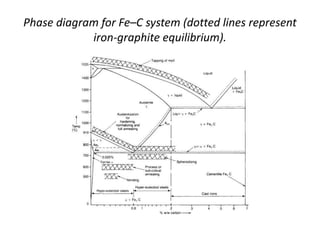
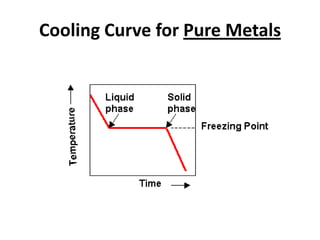
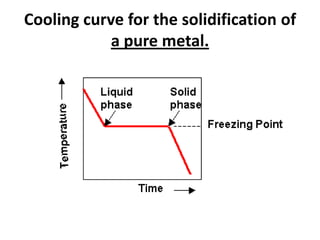
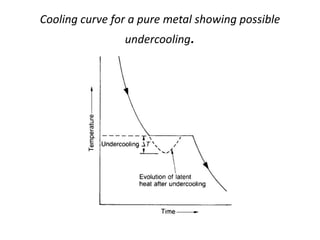
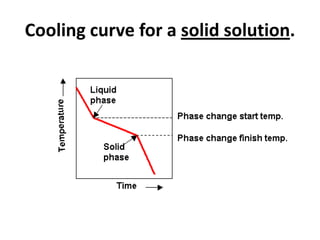
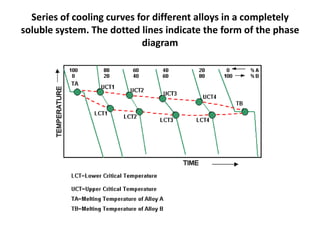
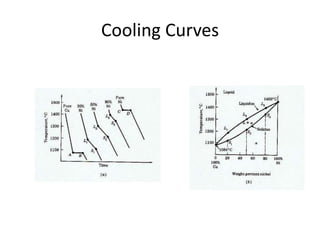
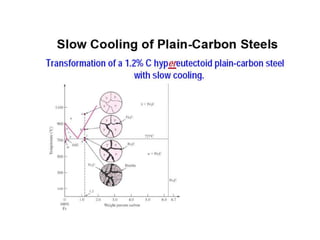
This document provides information about phase diagrams: [1] Phase diagrams graphically show the phases present in a material system at different temperatures and compositions. They can indicate properties like the number, type, and amount of phases. [2] There are several common types of phase diagrams including complete solid solution, eutectic, and peritectic diagrams. Cooling curves are also used to experimentally determine phase boundaries. 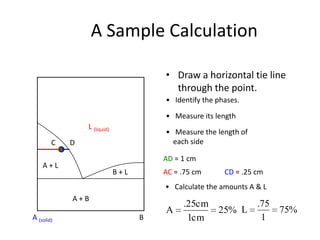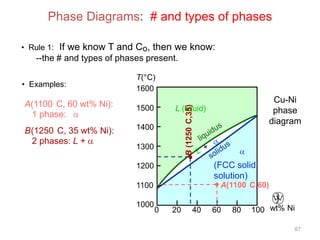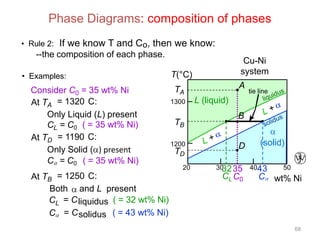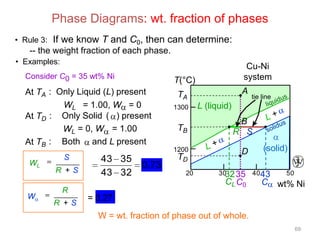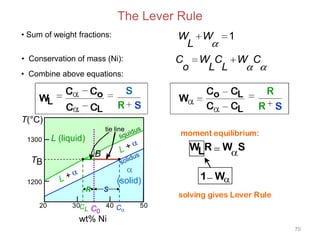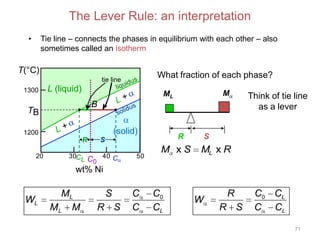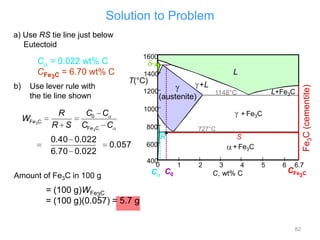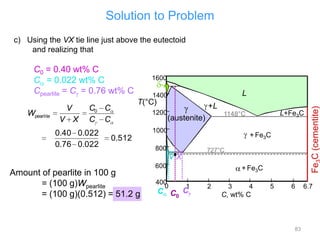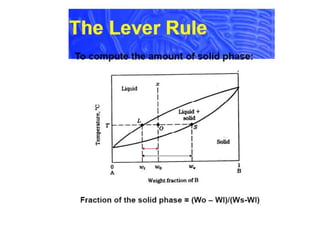[3] The phase rule relates the number of phases, components, and degrees of freedom in a system. Lever rule calculations use tie lines on phase diagrams to determine the composition and relative amounts of coexisting phases.

1. PHASE DIAGRAMS
Prof. H. K. Khaira
Professor
Deptt. of MSME
M.A.N.I.T., Bhopal

2. Contents
•
•
•
•
1. Phase diagram
2. Phase Rule
3. Lever Rule
Microstructure Development

3. Phase Diagrams

4. Phase
• Phase is a homogenous, physically distinct
and mechanically separable portion of the
material with a given chemical composition
and structure.

5. Phase diagrams
Properties of a materials depend on
1. Number of phases present
2. Type of phases present
3. Amount of phases present and
4. Form of the phases present
The Properties can be changed by altering these
quantities.
In order to make these changes, it is essential to
know the conditions under which these quantities
exist and the conditions under which a change in
phase will occur.

6. Phase diagrams
• The best method to record the data related
to phase changes in many alloy systems is in
the form of phase diagrams, also known as
equilibrium diagrams or constitutional
diagrams.

7. Phase diagrams
• In order to specify completely the state of a
system in equilibrium, it is necessary to specify
three independent variables.
• These variables, which are externally
controllable, are temperature, pressure and
composition.
• Phase diagram is the graphical presentation of
the phases present in a system under different
conditions of pressure, temperature and
composition.

8. Phase diagrams
• In metallurgical systems, the pressure is
usually taken as atmospheric pressure. Thus
the phase diagram shows the phases present
at different compositions and temperatures.

9. Phase diagrams
• With pressure assumed to be constant at
atmospheric pressure, the equilibrium diagram
indicates the structural changes due to variation
of temperature and composition.
• Phase diagrams show the phases present under
equilibrium conditions, that is, under conditions
in which there will be no change with time.
• Equilibrium conditions may be approached by
extremely slow heating and cooling, so that if a
phase change is to occur, sufficient time is
allowed.

10. Phase diagrams
The phase diagram in Figure
displays an alloy of two metals
which forms a solid solution at all
relative concentrations of the two
species

11. Phase diagrams
• Phase diagrams are usually plotted with
composition on X axis and the temperature
on Y axis,.

12. Types of Equilibrium Diagrams
• 1. Complete solid solution type
• 2. Eutectic type
• 3. Peritectic type

13. Complete solid solution type

14. Complete solid solution type
• The phase diagram in which both the
constituents are soluble in each other in solid
state at all compositions, is known as
complete solid solution type phase diagram.

15. Complete solid solution Diagram
The phase diagram in Figure
displays an alloy of two metals
which forms a solid solution at all
relative concentrations of the two
species

16. Nickel-Copper Phase Diagram

17. Germanium-Silicon Phase
Diagram

18. Eutectic Type

19. Eutectic Type
• It is a phase diagram containing eutectic
reaction.
• Eutectic reaction is :
L = α (s) + β (s)
In this reaction, a liquid phase (L) decomposes into
a mixture of two solid phases (α and β) on
cooling.

20. Eutectic Diagram

21. Tin-Lead Phase Diagram

22. Gold-Germanium Phase Diagram

23. Copper-Silver Phase Diagram

24. Peritectic Diagram
• It is a phase diagram containing peritectic
reaction.
• peritectic reaction :
L + α (s) = β (s)
• In peritectic reaction, a liquid (L) and a solid (α)
transform in to another solid (β) on cooling.

25. Phase diagram for Fe–C system (dotted lines represent
iron-graphite equilibrium).

26. Application of Phase Diagrams
• Phase diagram gives us
–
–
–
–
–
–
–
–
Overall Composition
Solidus
Liquidus
Limits of Solid Solubility
Chemical Composition of Phases at any temperature
Amount of Phases at any temperature
Invariant Reactions
Development of Microstructure

27. Overall Composition
• Concentration: Relative amounts of each
constituent
• It is the horizontal axis in all binary phase
diagrams
• The scale can be in weight %, atomic % or
mole %

28. Solidus and Solidus
• Solidus
– Temperature up to which alloy is completely solid
– Temperature at which liquefaction begins
• Liquidus
– Temperature up to which alloy is completely liquid
– Temperature at which solidification begins

29. Chemical Composition of Phases
• It is the chemical composition of each phase
in the system
• In a system having more than one phase, each
phase will have a unique chemical
composition which will be different from each
other, and will also be different from the
overall composition
• Not to be confused with overall composition

30. Invariant Reactions
•
•
•
•
•
Eutectic: L = α (s) + β (s); e.g., Pb-Sn
Peritectic: α (s) + L = β (s); e.g., Pb-In
Monotectic: L1 = α (s) + L2; e.g., Cu-Pb
Syntectic: L1 + L2 = α (s); e.g., Na-Zn
Metatectic: β (s) + α (s) = L1 e.g., U-Mn

31. Cooling Curve
• A cooling curve is a graphical plot of the
changes in temperature with time for a
material over the entire temperature range
through which it cools.

32. Cooling Curve for Pure Metals

33. Cooling Curve
• This is by far the most widely used
experimental method.
• It relies on the information obtained from
the cooling diagrams.
• In this method, alloys with different
compositions are melted and then the
temperature of the mixture is measured at a
certain time interval while cooling back to
room temperature.

34. Cooling Curve
• A cooling curve for each mixture is
constructed and the initial and final phase
change temperatures are determined. Then
these temperatures are used for the
construction of the phase diagrams

35. Cooling Curve
• Under equilibrium conditions, all metals
exhibit a definite melting or freezing point. If
a cooling curve is plotted for a pure metal. It
will show a horizontal line at the melting or
freezing temperature.

36. Cooling curve for the solidification of
a pure metal.

37. Cooling curve for a pure metal showing possible
undercooling.

38. Cooling curve for a solid solution.

39. Phase Diagram of alloy A+B

40. Series of cooling curves for different alloys in a completely
soluble system. The dotted lines indicate the form of the phase
diagram

41. Cooling Curves

42. The Phase Rule

43. The Phase Rule
Degree of freedom or Variance (f): the number of intensive variables
that can be changed independently without disturbing the number
of phases in equilibrium.
The phase rule: a general relation among the variance f, the number
of components c and the number of phases p at equilibrium for a
system of any composition.
f=c–p+2
43

45. Chapter 7
Physical Chemistry
The Phase Rule
(a)
(b)
The difference between (a) a single-phase solution, in which the
composition is uniform on a microscopic scale, and (b) a
dispersion, in which regions of one component are embedded in
a matrix of a second component.
45

46. Chapter 7
Physical Chemistry
The Phase Rule
Phase: a state of matter that is uniform throughout in chemical
composition and physical state. (Gibbs)
Number of phase (p):
Gas or gaseous mixture – single phase
Liquid – one, two and three phases
two totally miscible liquids – single phase
a slurry of ice and water – two phases
Solid – a crystal is a single phase
an alloy of two metals – two phases (immiscible)
- one phase (miscible)
46

50. Simple Example

51. Chapter 7
Physical Chemistry
H2O phase diagram: P — T
Region (s, l, g):
D
P / 10 5 Pa
218 atm
C
f=2, one phase
Y
I
solid
Line (OA, AD, AC):
liquid
S
f=1, two phases in
equilibrium
1 atm
R
0.00611
gas
A
Point (A):
O
0.0024 0.01
T3
Tf
99.974
Tb
t/℃
374.2
Tc
f=0, three phases in
equilibrium
51

52. Chapter 7
Physical Chemistry
One-component phase equilibrium
For a one-component system (pure water)
f＝1－p＋2＝3－p，(C＝1）
f ≥0, p ≥1, 3≥p≥1
p＝1，f＝2
p＝2，f＝1
p＝3，f＝0
52

53. Lever Rule

54. Lever Rule
• The compositions of the two coexisting phases at a
point in a two phase region is given by the points of
intersection of the tie line from that point with the
boundaries of the respective phases.
• The relative amounts of two coexisting phases at a
point are INVERSELY proportional to the distances of
the point from intersection points of the tie line from
the point with the phase boundaries.”
54

55. Translating This Statement
• “two coexisting phases”
Means you are in a 2 phase
region.
Pick an arbitrary point C.
• There are two phases at point C.
• These phases are A an B
• Hence Phases A and B will be
in equilibrium at point C
•
L
A+L
B+L
C
P
Q
A+B
A
B

56. Tie Lines
The line from A to B through C is a tie line.
A tie line is,
• An isothermal line
• That connects two equilibrium phases

57. Translating This Statement
The tie line from point C
intersect boundaries of
phase A and B at 0% A and
0% B respectively.
Hence the composition of
phase A will be 0% B or
pure A.
Similarly, the composition of B
will be pure B or 0% A.
L
A+L
B+L
C
A+B
A
The distances are AC and AB
B

58. Translating This Statement
L
A+L
“The intercepts of the tie line
with the phase boundaries
A and B are PA and CQ
respectively.
B+L
C
P
Q
A+B
A
B

59. Translating This Statement
The intercepts of the tie line
with the phase boundaries
A and B are CA and CB
respectively.
L
A+L
B+L
C
A+B
A
B

60. Translating This Statement
• “The amounts . . . Are
inversely proportional”
Means AC / AB is the
fraction of B
L
B=
And, CB / AB is the fraction
of A
A+L
B+L
A=
C
A+B
A
B

61. A Sample Calculation
• Draw a horizontal tie line
through the point.
• Identify the phases.
• Measure its length
L (liquid)
C
• Measure the length of
each side
D
AD = 1 cm
A+L
B+L
AC = .75 cm
CD = .25 cm
• Calculate the amounts A & L
A+B
A (solid)
B
A
.25cm
1cm
25% L
.75
1
75%

62. A more complex system . . .
• Draw a tie line.
• Identify the phases.
• Measure the line lengths.
• Calculate the amounts of
each phase present.
A = Li2O-B2O3
B = Li2O-2B2O3
C
A
CB = .562 cm
AC = .188 cm
AB = .75 cm
B
A
.562
.75
75% B
.188
.75
25%

63. One Last Note.
C
If a point is in a single
phase region (including a
solid solution), NO tie line
is used. There is 100% of
that phase.

64. Summary
• The lever rule is used to calculate the relative percents of
each phase when 2 or more phases are present.
• The first step in lever rule calculation is to draw a tie line
through the composition.
• Next one measures the lengths of the tie line, and the
distance from the composition to each phase.
• The relative concentration of a phase is proportional to the
distance from the other phase to the composition, divided
by the length of the tie line. (Opposite length / total
length)

65. 65

66. Cu-Ni Phase Diagram: T vs. c (wt% or at%)
• Tell us about phases as function of T, Co, P.
• For this course:
--binary systems: just 2 components.
--independent variables: T and Co (P = 1atm is always used).
-- isomorphous
i.e., complete
solubility of one
component in
another; a phase
field extends from
0 to 100 wt% Ni.
T(°C)
1600
1500
L (liquid)
Contains 2 Phases
1. L
2.
There are 3 phase fields
1. L
2. L +
3.
1400
1300
1200
(FCC solid
1100
1000
solution)
0
20
40
60
80
100 wt% Ni
66

67. Phase Diagrams: # and types of phases
• Rule 1:
If we know T and Co, then we know:
--the # and types of phases present.
A(1100 C, 60 wt% Ni):
1 phase:
B(1250 C, 35 wt% Ni):
2 phases: L +
1500
L (liquid)
1400
1300
(FCC solid
solution)
1200
A(1100 C,60)
1100
1000
Cu-Ni
phase
diagram
B (1250 C,35)
• Examples:
T(°C)
1600
0
20
40
60
80
100 wt% Ni
67

68. Phase Diagrams: composition of phases
• Rule 2:
If we know T and Co, then we know:
--the composition of each phase.
• Examples:
Consider C0 = 35 wt% Ni
At TA = 1320 C:
Only Liquid (L) present
CL = C0 ( = 35 wt% Ni)
At TD = 1190 C:
Only Solid ( ) present
C = C0 ( = 35 wt% Ni)
At TB = 1250 C:
Both and L present
CL = C liquidus ( = 32 wt% Ni)
C = C solidus ( = 43 wt% Ni)
Cu-Ni
system
T(°C)
A
TA
1300
TB
1200
TD
20
tie line
L (liquid)
B
D
30 35
32
C L C0
(solid)
4043
C
50
wt% Ni
68

69. Phase Diagrams: wt. fraction of phases
• Rule 3:
If we know T and C0, then can determine:
-- the weight fraction of each phase.
• Examples:
Consider C0 = 35 wt% Ni
T(°C)
At TA : Only Liquid (L) present
WL = 1.00, W = 0
At TD : Only Solid ( ) present
WL = 0, W = 1.00
At TB : Both and L present
WL
W
S
R +S
R
R +S
43 35
43 32
Cu-Ni
system
0.73
A
TA
1300
TB
1200
TD
20
tie line
L (liquid)
B
R S
D
30 35
32
CL C0
(solid)
40 43
C
50
wt% Ni
= 0.27
W = wt. fraction of phase out of whole.
69

70. The Lever Rule
• Sum of weight fractions:
W W
L
• Conservation of mass (Ni):
1
C
W C W C
o
L L
• Combine above equations:
T(°C)
tie line
1300
WLR W S
B
TB
(solid)
1200
R
20
moment equilibrium:
L (liquid)
30C
L
S
C0 40 C
1 W
solving gives Lever Rule
50
wt% Ni
70

71. The Lever Rule: an interpretation
•
Tie line – connects the phases in equilibrium with each other – also
sometimes called an isotherm
T(°C)
What fraction of each phase?
tie line
1300
L (liquid)
B
TB
(solid)
1200
R
20
M
ML
30C
L
R
S
C0 40 C
50
M xS
Think of tie line
as a lever
S
ML x R
wt% Ni
WL
ML
ML M
S
R S
C
C
C0
CL
W
R
R S
C0 CL
C CL
71

72. Phase and Microstructure (equilibrium)
Example: Cooling in Cu-Ni Binary
• Consider microstuctural
changes that accompany
the cooling of a
C0 = 35 wt% Ni alloy
T(°C) L (liquid)
130 0
L: 35 wt% Ni
: 46 wt% Ni
• From liquid, solid phase nucleates.
A
35
32
• From solid, other phases can nucleate.
• Like ice, many grains of solid form.
L: 35wt%Ni
B
C
46
43
D
24
L: 32 wt% Ni
36
120 0
: 43 wt% Ni
E
L: 24 wt% Ni
• wt% of SOLUTE given by line dropped
from boundaries
: 36 wt% Ni
• Fraction of PHASES present given by
the “lever rule”.
• Microstructure different depending on
cool slowly or quench.
(solid)
110 0
20
30
35
C0
40
50
wt% Ni
72

73. Binary-Eutectic Systems
has a special composition
with a minimum melting T.
• Ex: Cu-Ag
3 single-phase regions
(L, , )
• Limited solubility
: mostly Cu
: mostly Ag
• TE: no liquid below TE.
• cE: composition for min.
melting T (Eutectic).
Cu-Ag
system
T(°C)
1200
L (liquid)
1000
L+
TE 800
779°C
8.0
L+
71.9 91.2
600
400
200
0
20
40
100
60 CE 80
C , wt% Ag
Eutectic: direct from liquid to 2-phase solid upon cooling: L
cooling
L(71.9 wt% Ag)
(8.0 wt% Ag)
(91.2 wt% Ag)
+
heating
73

74. Example 2: Pb-Sn Eutectic System
• For a 40 wt% Sn-60 wt% Pb alloy at 220 C, determine:
-- phases present:
+L
T(°C)
-- phase compositions
C = 17 wt% Sn
CL = 46 wt% Sn
-- relative amt of phases
300
L (liquid)
L+
220
200
CL - C0
46 - 40
=
W =
= 0.21
CL - C
46 - 17
100
C0 - C
23
=
= 0.79
WL =
CL - C
29
R
S
L+
183 C
+
0
17 20
C
40 46 60
80
C0 CL C, wt% Sn
100
74

75. Example 2: Pb-Sn Eutectic System
• For a 40 wt% Sn-60 wt% Pb alloy at 220 C, determine:
-- phases present:
+L
T(°C)
-- phase compositions
C = 17 wt% Sn
CL = 46 wt% Sn
-- relative amt of phases
300
L (liquid)
L+
220
200
CL - C0
46 - 40
=
W =
= 0.21
CL - C
46 - 17
100
C0 - C
23
=
= 0.79
WL =
CL - C
29
R
S
L+
183 C
+
0
17 20
C
40 46 60
80
C0 CL C, wt% Sn
100
75

76. Solder for electronics
Example 1: Lead-Tin (Pb-Sn) Eutectic Diagram
• For a 40wt%Sn-60wt%Pb alloy at 150oC, determine...
--phases present: +
--compositions of phases:
C = 11 wt% Sn
T(°C)
300
L (liquid)
C = 99 wt% Sn
-- relative amount Use the
of each phase: “Lever Rule” 200
C - C0
S
=
W =
R+S
C -C
99 - 40
99 - 11
W = R =
R+S
40 - 11
=
99 - 11
=
59
= 0.67
88
C0 - C
C -C
150
100
L+
L+
183°C
18.3
61.9
R
97.8
S
+
=
=
29
= 0.33
88
0 11 20
C
40
C0
60
80
C, wt% Sn
99100
C
Adapted from Fig.
10.8, Callister & Rethwisch
3e.
76

77. Example 2: Pb-Sn Eutectic System
• For a 40 wt% Sn-60 wt% Pb alloy at 220 C, determine:
-- phases present:
+L
T(°C)
-- phase compositions
C = 17 wt% Sn
CL = 46 wt% Sn
-- relative amt of phases
300
L (liquid)
L+
220
200
CL - C0
46 - 40
=
W =
= 0.21
CL - C
46 - 17
100
C0 - C
23
=
= 0.79
WL =
CL - C
29
R
S
L+
183 C
+
0
17 20
C
40 46 60
80
C0 CL C, wt% Sn
100
77

78. Microstructure “below” Eutectic (hypoeutectic)
• For alloys for 18.3wt%Sn < Co < 61.9wt%Sn
• Result: a crystals and a eutectic microstructure
T(°C)
L: C0 wt% Sn
L
300
L
C = 18.3 wt% Sn
CL = 61.9 wt% Sn
W = S = 0.50
R+S
WL = (1- W ) = 0.50
L
Pb-Sn
system
L+
200
R
TE
R
100
L+
S
+
S
• Just below TE :
primary
eutectic
eutectic
0
20
18.3
Adapted from Fig.
10.16, Callister &
Rethwisch 3e.
• Just above TE :
40
60
61.9
80
C, wt% Sn
100
97.8
C = 18.3 wt% Sn
C = 97.8 wt% Sn
W = S = 0.73
R+S
W = 0.27
78

79. Solder: Lead-Tin (Pb-Sn) microstructure
L
For 50 wt% Pb alloy:
• Lead-rich phase (dark)
• Lamellar eutectic structure
of Sn-rich phase (light).
L+
+
* Why is Liquid-phase ~62.9wt%Sn and -phase ~16.3wt%Sn at 180 C?
* For fraction of total phase (both eutectic and primary), use the Lever Rule.
79

80. Hypoeutectic & Hypereutectic
Adapted from Fig. 10.8,
Callister & Rethwisch 3e.
(Figs. 10.14 and
10.17 from Metals
Handbook, 9th
ed., Vol.
9, Metallography and
Microstructures, Amer
ican Society for
Metals, Materials
Park, OH, 1985.)
80

81. Example Problem Steel
For a 99.6 wt% Fe-0.40 wt% C steel at a
temperature just below the
eutectoid, determine the following:
a) The compositions of Fe3C and ferrite ( ).
b) The amount of cementite (in grams) that
forms in 100 g of steel.
c) The amounts of pearlite and proeutectoid
ferrite ( ) in the 100 g.
81

82. Solution to Problem
a) Use RS tie line just below
Eutectoid
b)
Use lever rule with
the tie line shown
WFe 3C
R
R S
1600
T(°C)
1200
C0 C
CFe 3C C
0.40 0.022
6.70 0.022
L
1400
+L
1000
+ Fe3C
800
727°C
R
0.057
S
+ Fe3C
600
400
0
Amount of Fe3C in 100 g
L+Fe3C
1148°C
(austenite)
Fe3C (cementite)
C = 0.022 wt% C
CFe3C = 6.70 wt% C
C C0
1
2
3
4
C, wt% C
5
6
6.7
CFe
3C
= (100 g)WFe3C
= (100 g)(0.057) = 5.7 g
82

83. Solution to Problem
c) Using the VX tie line just above the eutectoid
and realizing that
C0 = 0.40 wt% C
C = 0.022 wt% C
Cpearlite = C = 0.76 wt% C
V X
T(°C)
C0 C
C C
0.40 0.022
0.76 0.022
L
1400
1200
+L
L+Fe3C
1148°C
(austenite)
1000
+ Fe3C
0.512
800
727°C
VX
Amount of pearlite in 100 g
= (100 g)Wpearlite
= (100 g)(0.512) = 51.2 g
600
400
0
+ Fe3C
1
C C0 C
2
3
4
5
6
C, wt% C
83
Fe C (cementite)
Wpearlite
V
1600
6.7

90. Example Problem
• One kilogram of an alloy of 70% Pb and 30% Sn is slowly
cooled from 300ºC. Calculate the following:
• a) Weight % of liquid and α at 250ºC
• b) Chemical composition of the liquid and α at 250ºC
• c) Weight % of the liquid and α just above the eutectic
temperature
• d) Chemical composition of the liquid and α at just above the
eutectic temperature
90

92. Summary
Lever Rule
• Lever Rule is useful to determine:
- the composition of each phase,
- and the wt% of each phase
•
92

93. Microstructure Development
• The microstructure developed depends on the
overall composition and the cooling rate

94. Composition dependence of
microstructure

95. Composition dependence of
microstructure

96. Composition dependence of
microstructure

97. Composition dependence of
microstructure

98. Composition dependence of
microstructure

99. Phase diagram for Pb–Sn system. Alloy 1: 63Sn–37Pb,
Alloy 2: 70Pb–30Sn, Alloy 3: 70Sn–30Pb.