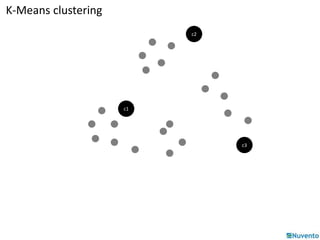
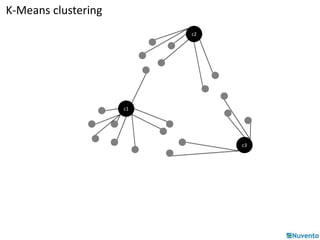
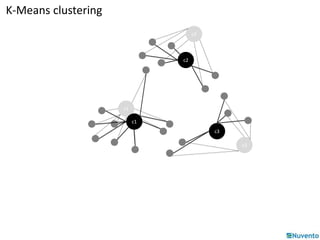
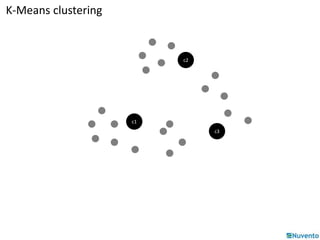
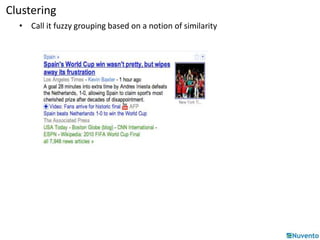
K-Means clustering is an algorithm that partitions data points into k clusters based on their distances from initial cluster center points. It is commonly used for classification applications on large datasets and can be parallelized by duplicating cluster centers and processing each data point independently. Mahout provides implementations of K-Means clustering and other algorithms that can operate on distributed datasets stored in Hadoop SequenceFiles.

1. K-Means Clustering

2. Scale!
• Scale to large datasets
– Hadoop MapReduce implementations that scales linearly
with data.
– Fast sequential algorithms whose runtime doesn’t depend
on the size of the data
– Goal: To be as fast as possible for any algorithm
• Scalable to support your business case
– Apache Software License 2
• Scalable community
– Vibrant, responsive and diverse
– Come to the mailing list and find out more

3. History of Mahout
• Summer 2007
– Developers needed scalable ML
– Mailing list formed
• Community formed
– Apache contributors
– Academia & industry
– Lots of initial interest
• Project formed under Apache Lucene
– January 25, 2008

4. Where is ML Used Today
• Internet search clustering
• Knowledge management systems
• Social network mapping
• Taxonomy transformations
• Marketing analytics
• Recommendation systems
• Log analysis & event filtering
• SPAM filtering, fraud detection

5. Clustering
• Call it fuzzy grouping based on a notion of similarity

6. Mahout Clustering
• Plenty of Algorithms: K-Means,
Fuzzy K-Means, Mean Shift,
Canopy, Dirichlet
• Group similar looking objects
• Notion of similarity: Distance measure:
– Euclidean
– Cosine
– Tanimoto
– Manhattan

7. Classification
• Predicting the type of a new object based on its features
• The types are predetermined
Dog Cat

8. Mahout Classification
• Plenty of algorithms
– Naïve Bayes
– Complementary Naïve Bayes
– Random Forests
– Logistic Regression (SGD)
– Support Vector Machines (patch ready)
• Learn a model from a manually classified data
• Predict the class of a new object based on its
features and the learned model

9. Understanding data - Vectors
X = 5 , Y = 3
(5, 3)
Y
X
• The vector denoted by point (5, 3) is simply
Array([5, 3]) or HashMap([0 => 5], [1 => 3])

10. Representing Vectors – The basics
• Now think 3, 4, 5, ….. n-dimensional
• Think of a document as a bag of words.
“she sells sea shells on the sea shore”
• Now map them to integers
she => 0
sells => 1
sea => 2
and so on
• The resulting vector [1.0, 1.0, 2.0, … ]

11. Vectors
• Imagine one dimension for each word.
• Each dimension is also called a feature
• Two techniques
– Dictionary Based
– Randomizer Based

12. K-Means clustering
• K-means clustering is a classical clustering algorithm that uses an
expectation maximization like technique to partition a number of data points
into k clusters.
• K-means clustering is commonly used for a number of classification
applications.
• It is often run on extremely large data sets, on the order of hundreds of
millions of points and tens of gigabytes of data.
• Because k-means is run on such large data sets, and because of certain
characteristics of the algorithm, it is a good candidate for parallelization.

13. K-Means clustering
• At its simplest, the algorithm is given as inputs a set of n d-dimensional points
and a number of desired clusters k.
• For the purposes of this explanation, we will consider points in a Euclidean
space.
• However, the clustering algorithm will work in any space provided a distance
metric is given as input as well.
• Initially, k points are chosen as cluster centers.
• There is no fixed way to determine these initial points, instead a number of
heuristics are used, most commonly, k-points are chosen at random from the
sample of n points.
• Once the k initial centers are chosen, the distance is calculated from every point
in the set to each of the k centers and each point is assigned to the particular
cluster center whose distance is closest.
• Using this assignation of points to cluster centers, each cluster center is
recalculated as the centroid of its member points.
• This process is then iterated until convergence is reached.
• That is, points are reassigned to centers, and centroids recalculated until the k
cluster centers shift by less than some delta value.
• Because of the way k-means works it has the weakness that it can converge to a
local optimum but not a global optimum.
• This happens when the initial k center points are chosen badly.

14. Pseudocode
iterate {
Compute distance from all points to all k-centers
Assign each point to the nearest k-center
Compute the average of all points assigned to all specific k-centers
Replace the k-centers with the new averages
}

15. c1
c2
c3
K-Means clustering

16. c1
c2
c3
K-Means clustering

17. c1
c2
c3
c1
c2
c3
K-Means clustering

18. c1
c2
c3
K-Means clustering

19. Parallelizing k-means
• In order to parallelize k-means, we want to come up with a scheme where
we can operate on each point in the data set independently.
• In the first step of the iterative process of k-means, it is necessary to
compute the distance from each point to each of the k cluster centers and
assign that point to the cluster with the minimum distance.
• Thus, there is a small amount of shared data – namely the cluster centers.
• However, this is small in comparison to the number of data points.
• So the parallelization scheme involves duplicating the cluster centers,
however once this is duplicated each data point can be operated on
independently of the others and we can gain a nice speedup.

20. Step 1 – Convert dataset into a Hadoop Sequence File
• SGML files
– $ mkdir –p /reuters $ cd reuters-sgm && tar xzf
../reuters21578.tar.gz && cd .. && cd ..
• Extract content from SGML to text file
– $ mahout org.apache.lucene.benchmark.utils.ExtractReuters
reuters reuters/out

21. Step 1 – Convert dataset into a Hadoop Sequence File
• Use seqdirectory tool to convert text file into a
Hadoop Sequence File
– $ mahout seqdirectory
-i reuters/out
-o reuters/seqdir
-c UTF-8
-chunk 5

22. Hadoop Sequence File
• Sequence of Records, where each record is a <Key, Value> pair
– <Key1, Value1>
– <Key2, Value2>
– …
– …
– …
– <Keyn, Valuen>
• Key and Value needs to be of class org.apache.hadoop.io.Text
– Key = Record name or File name or unique identifier
– Value = Content as UTF-8 encoded string
• TIP: Dump data from your database directly into Hadoop Sequence Files

23. Writing to Sequence Files
Configuration conf = new Configuration();
FileSystem fs = FileSystem.get(conf);
Path path = new Path("testdata/part-00000");
SequenceFile.Writer writer = new SequenceFile.Writer(
fs, conf, path, Text.class, Text.class);
for (int i = 0; i < MAX_DOCS; i++)
writer.append(new Text(documents(i).Id()),
new Text(documents(i).Content()));
}
writer.close();

24. Generate Vectors from Sequence Files
• Steps
1. Compute Dictionary
2. Assign integers for words
3. Compute feature weights
4. Create vector for each document using word-integer mapping
and feature-weight
Or
• Simply run $ mahout seq2sparse

25. Generate Vectors from Sequence Files
• $ mahout seq2sparse
-i reuter/seqdir/
-o reuters/sparse
• Important options
– Ngrams
– Lucene Analyzer for tokenizing
– Feature Pruning
• Min support
• Max Document Frequency
• Min LLR (for ngrams)
– Weighting Method
• TF v/s TFIDF
• lp-Norm
• Log normalize length

26. Start K-Means clustering
• $ mahout kmeans
-i reuters/sparse/tfidf/
-c reuters-kmeans-clusters
-o reuters-kmeans
-dm org.apache.mahout.distance.CosineDistanceMeasure –cd 0.1
-x 10 -k 20 –ow
• Things to watch out for
– Number of iterations
– Convergence delta
– Distance Measure
– Creating assignments

27. Inspect clusters
• $ bin/mahout clusterdump
-s reuters-kmeans/clusters-9
-d reuters-out-seqdir-sparse-kmeans/dictionary.file-0
-dt sequencefile -b 100 -n 20
Typical output
:VL-21438{n=518 c=[0.56:0.019, 00:0.154, 00.03:0.018, 00.18:0.018, …
Top Terms:
iran => 3.1861672217321213
strike => 2.567886952727918
iranian => 2.133417966282966
union => 2.116033937940266
said => 2.101773806290277
workers => 2.066259451354332
gulf => 1.9501374918521601
had => 1.6077752463145605
he => 1.5355078004962228

28. FAQs
• How to get rid of useless words
• How to see documents to cluster assignments
• How to choose appropriate weighting
• How to run this on a cluster
• How to scale
• How to choose k
• How to improve similarity measurement

29. FAQs
• How to get rid of useless words
– Use StopwordsAnalyzer
• How to see documents to cluster assignments
– Run clustering process at the end of centroid generation using –cl
• How to choose appropriate weighting
– If its long text, go with tfidf. Use normalization if documents different in
length
• How to run this on a cluster
– Set HADOOP_CONF directory to point to your hadoop cluster conf
directory
• How to scale
– Use small value of k to partially cluster data and then do full clustering
on each cluster.

30. FAQs
• How to choose k
– Figure out based on the data you have. Trial and error
– Or use Canopy Clustering and distance threshold to figure it
out
– Or use Spectral clustering
• How to improve Similarity Measurement
– Not all features are equal
– Small weight difference for certain types creates a large
semantic difference
– Use WeightedDistanceMeasure
– Or write a custom DistanceMeasure

31. More clustering algorithms
• Canopy
• Fuzzy K-Means
• Mean Shift
• Dirichlet process clustering
• Spectral clustering.

32. End of session
Day – 4: K-Means Clustering