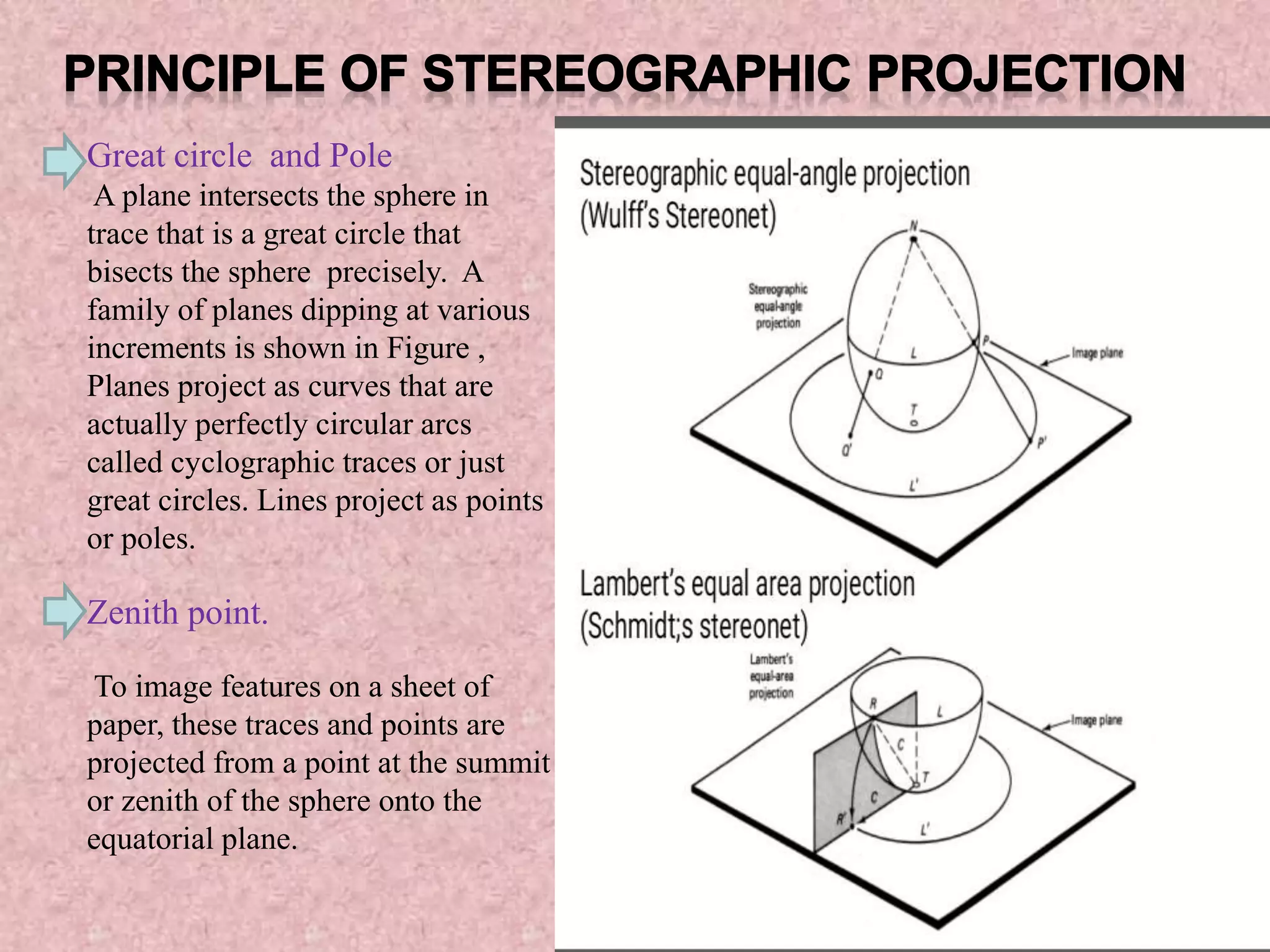
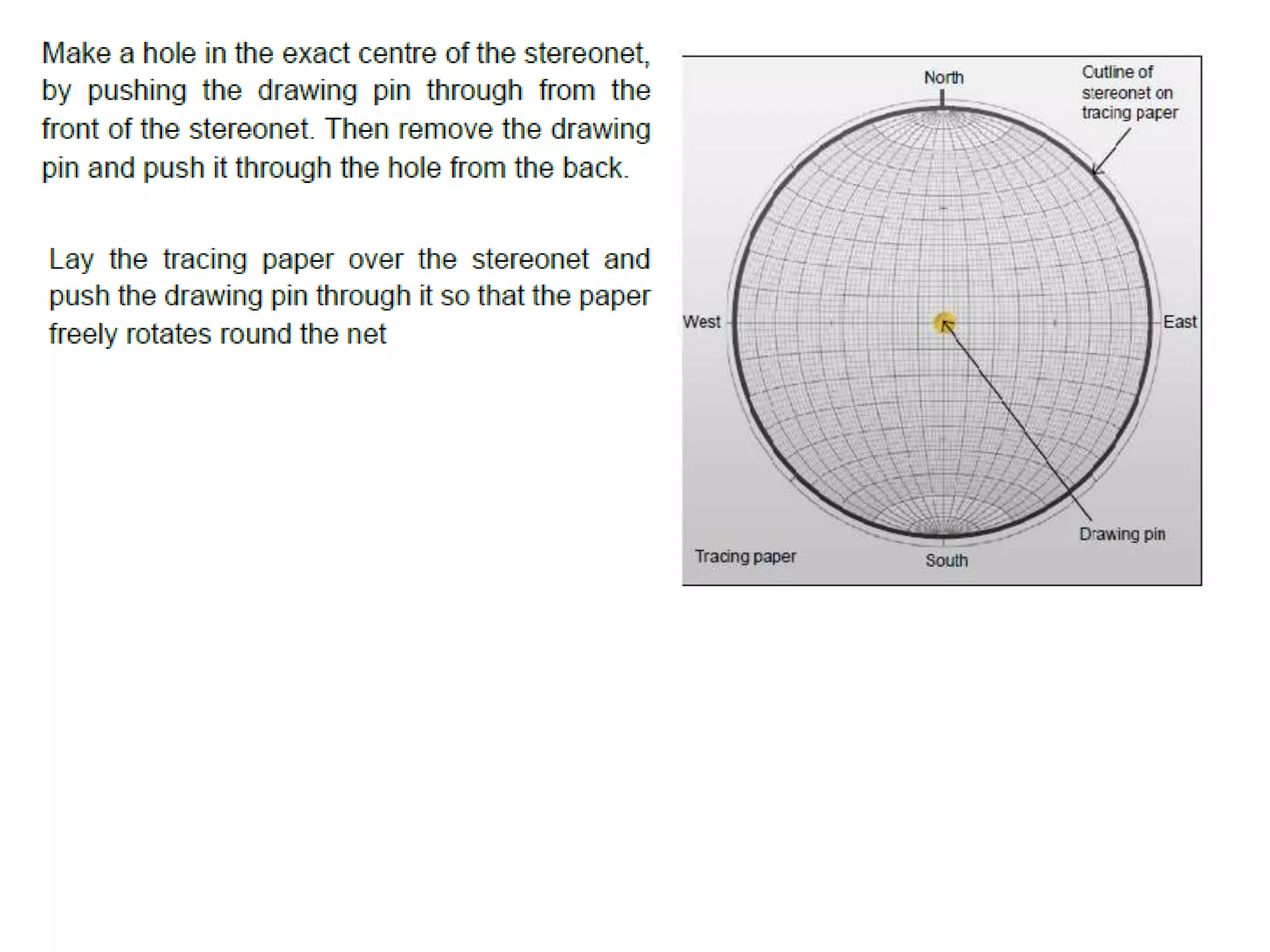
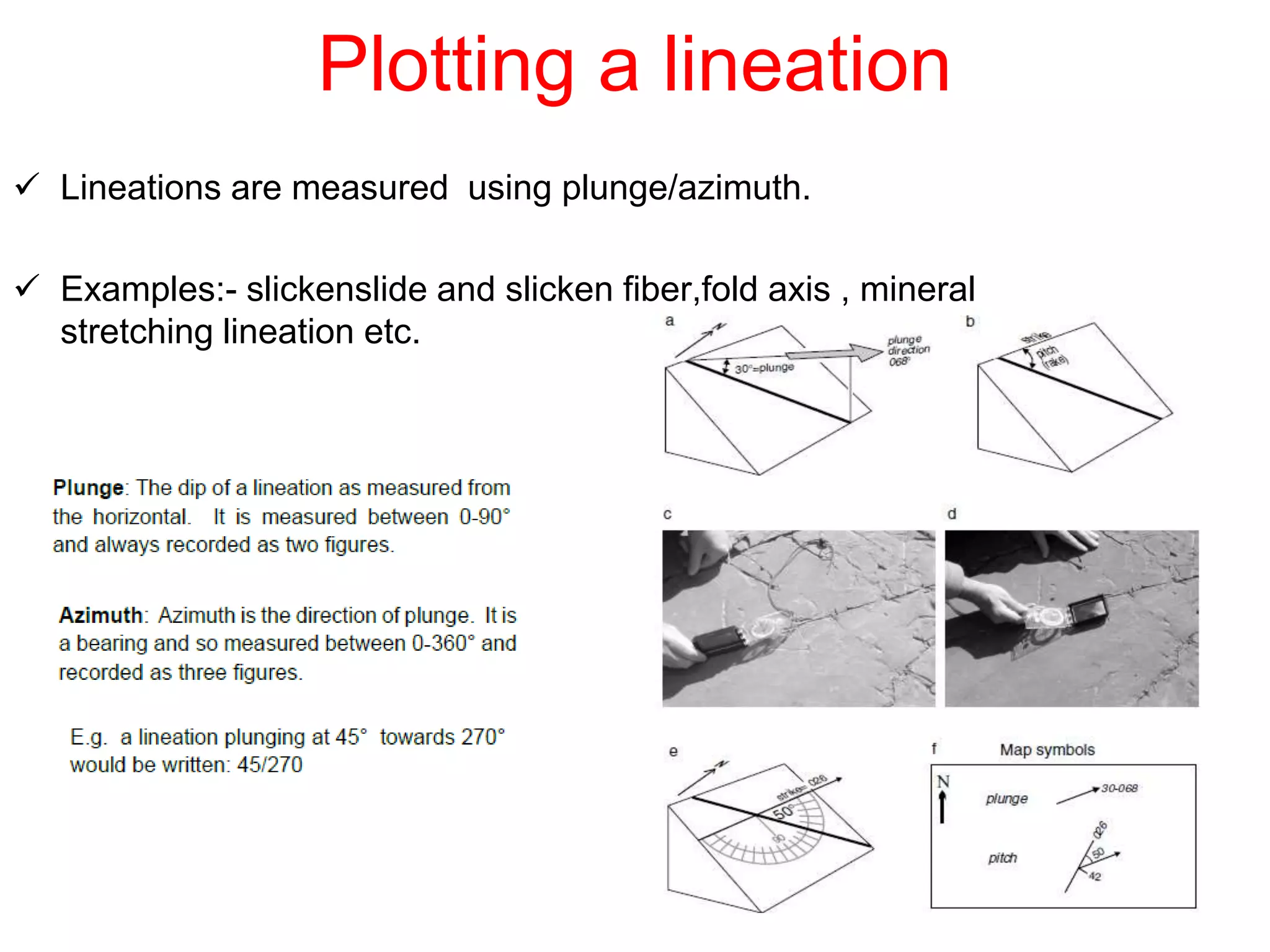
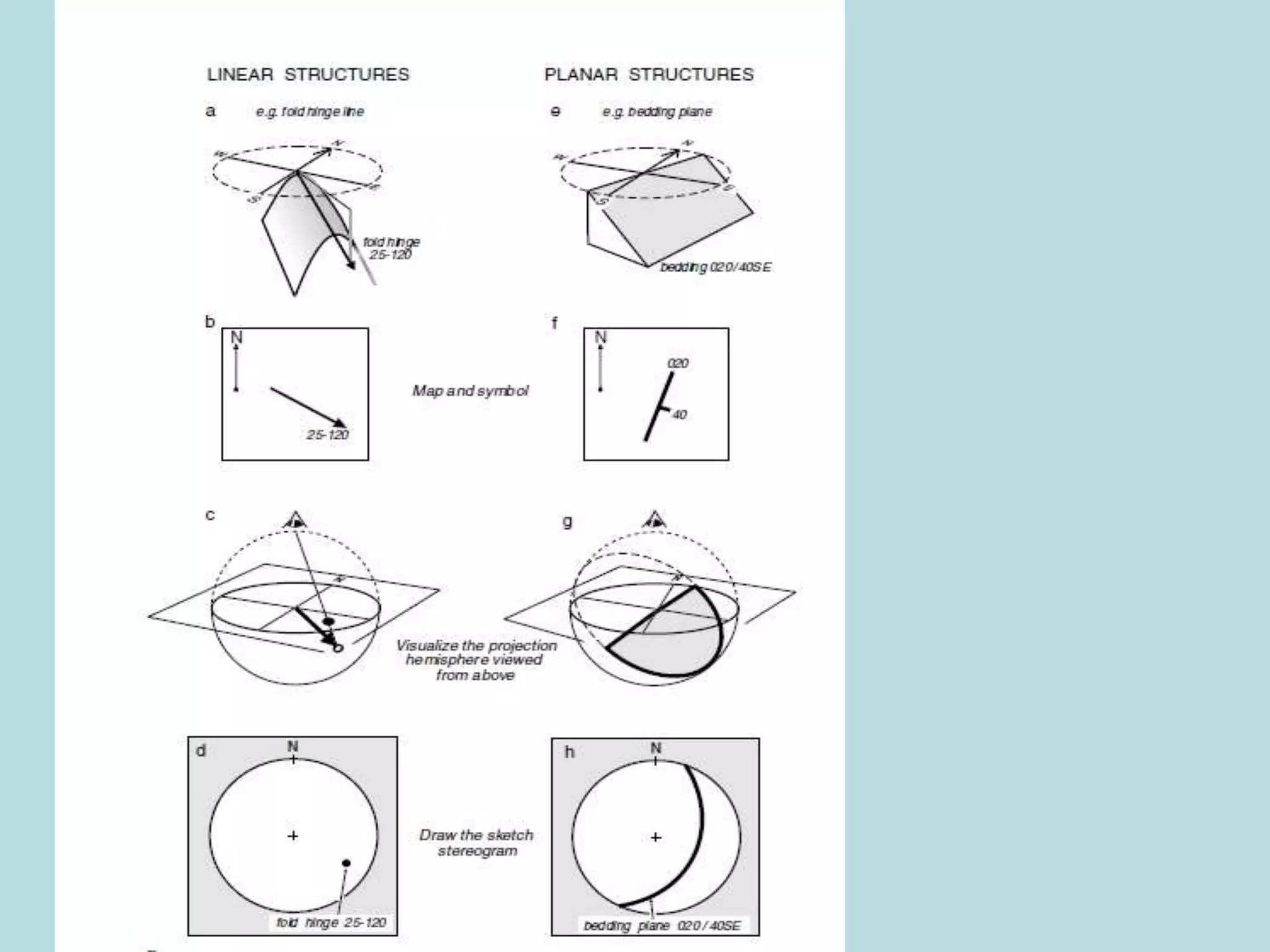
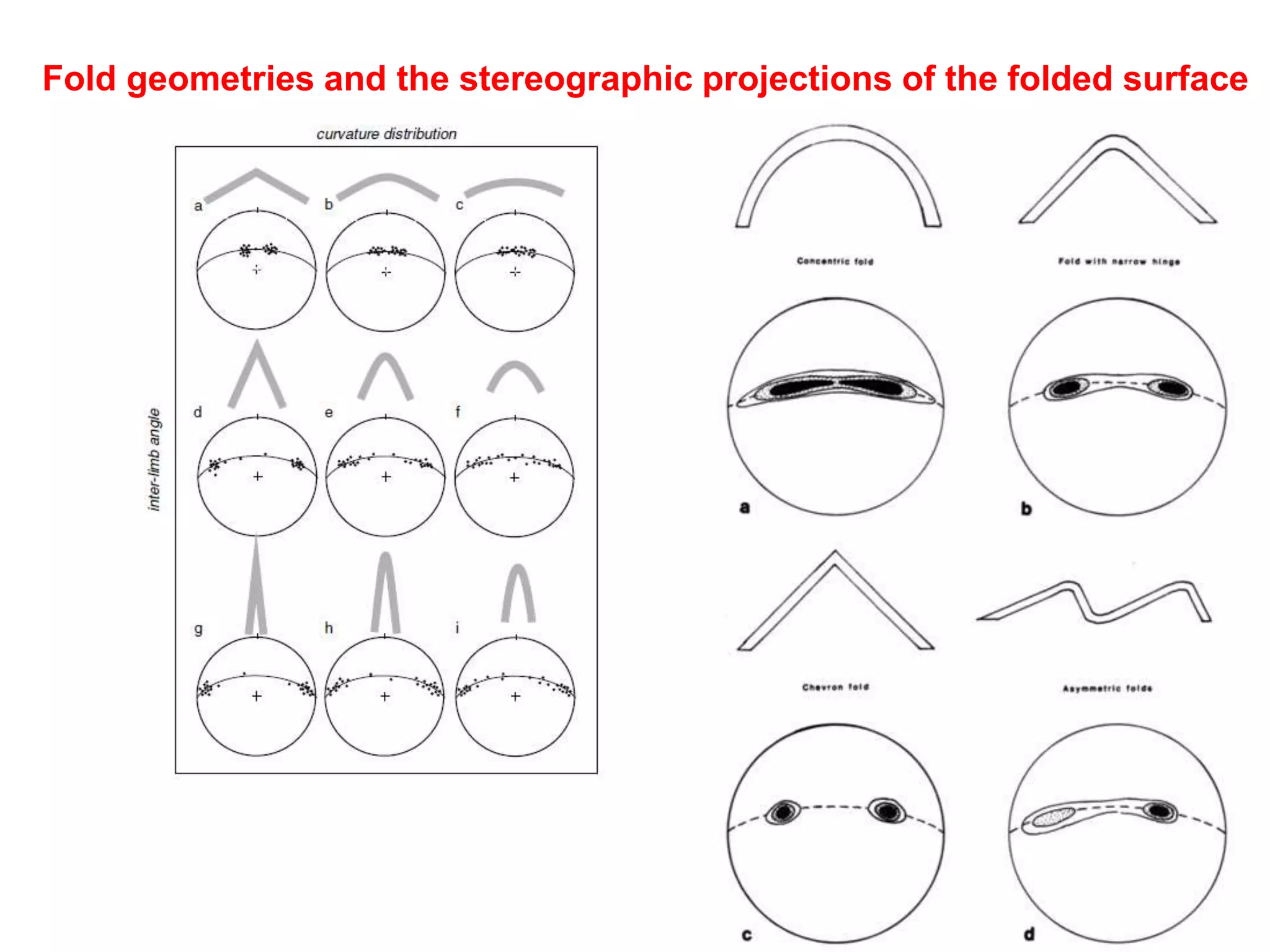
Stereographic projection is a powerful method for representing planar and linear geological features by plotting their orientations on a stereonet. It allows geologists to visualize and analyze structural data. A stereonet is a lower hemisphere projection where great circles represent planar features like bedding planes, and points represent linear features like fold axes. Various geological data can be plotted on a stereonet, including strike and dip of planes, plunge and trend of linear features, and poles to planes. This allows interpreting relationships between structures and reconstructing geometries, like determining the orientation of an ore body in relation to a dike intruding folded beds. Stereographic projection is an invaluable tool in structural geology.

1. DR. HARISINGH GOUR
VISHWAVIDYALAYA SAGAR (M.P.)
(A Central University )
UNDER GUIDENCE OF :-
PROF P.K KATHAL &
DR GAURAV K SINGH
SEMINAR TOPIC : STEREOGRAPHIC PROJECTION
POORVA PANDEY
Y1 9251026
Mtech 1st sem
1

2. CONTENT
Content Page no
1) Introduction of stereographic projection 01 -02
2) Idea about stereonet 03-04
3) Principle of stereographic projection 05 -06
4) construction of stereographic 07- 08
projection on stereonet
5) How to plot a plane 09
6) How to plot a lineation 10
7) how to plot a pole 11
8) How to plot a plunge 12
9) Geometrical represation of planer and linear structure 13
10) About pi and ß diagram 14
11) stereographic projection of folded surface 15
12) some problems related to stereographic projection 16

3. INTRODUCTION
Stereographic projection is a powerful method for solving geometric problems in
structural geology. Unlike structure contouring and other map-based techniques, it
preserves only the orientation of lines and planes with no ability to preserve position
relationships. However, it is extremely useful, as orientation problems are very common
in structural geology. Used by crystallographers as a tool for representing variations in
crystal form
There are several varieties of stereonet available.
Wulff net - which is used for the construction of the true, or equal-angle
stereographic projection .
Schmidt net - which constructs an equal area projection.

4. General idea about stereonet : -
FIGURE 1 FIGURE 2

5. Great circle and Pole
A plane intersects the sphere in
trace that is a great circle that
bisects the sphere precisely. A
family of planes dipping at various
increments is shown in Figure ,
Planes project as curves that are
actually perfectly circular arcs
called cyclographic traces or just
great circles. Lines project as points
or poles.
Zenith point.
To image features on a sheet of
paper, these traces and points are
projected from a point at the summit
or zenith of the sphere onto the
equatorial plane.

8. A
B
C
• A stereonet is a lower hemisphere graph
on to which a variety of geological data
can be plotted .stereonet are used in
many different branches of geology and
can be used in a range of ways beyond
those which are discussed here
,stereographic projection involves
plotting 34D data (planner and linear )on
to the 2D surface ,where it can be
manipulated and interpreted .
• Imagine a sphere with lines lattitude and
longitude marked on it ,A stereonet is the
plane of projection of the lower half of the
sphere –it is a lower hemisphere graph
• Imagine a plane cutting through the
centre of a lower hemisphere ( figure A)
,The stereonet forms the surface of this
lower hemisphere looking from above
where the plane touches the edge of the
lower hemisphere is an arc is projected
back up on the stereonet to form a great
circle ( figure B)
and figure C Shows the resulting
plot.

9. HOW TO PLOT A PLANE
Plot a plane with strike/dip as 090/40S

10.  Lineations are measured using plunge/azimuth.
 Examples:- slickenslide and slicken fiber,fold axis , mineral
stretching lineation etc.
Plotting a lineation

13. Plotting a pole
 The pole to a plane is an imaginary line
perpendicular to the plane.
 A stereonet with poles is known as a Pi (π) plot.
Plotting a pole to 055/20 SE.
● Mark on the strike reading 055°
● Note which way the plane is dipping, then rotate the
tracing paper round until this mark is aligned with north on
the stereonet.
● Find the great circle of the plane by counting along the
equator from the primitive. Count in from the direction of dip
as marked on the tracing paper (in this case SE) along the
equator line 20°.
● Count a further 90° through the centre of the net and mark
a point – this is the pole to the plane

14. Pi-plots and folds on stereonets
• Poles are a common way of plotting folded
bedding on stereonets. The distribution of poles on the stereonet
gives information on the fold’s geometry including estimates of the
fold axis and the fold axial plane.
• In this simple example the beds all have the same strike, it is only
their dip that varies round the fold.

15. Fold geometries and the stereographic projections of the folded surface

17. Problems in Stereographic projection
 Apparent dip of a bed is 26 degreeNE on a cliff trending N60degreeE.The
same bed has an apperent dip of 19degree SW on a cliff trending
N10degreeE. Find the strike and true dip of the bed.

18. solution

19.  An ore body occures in the plunging trough formed by a basic dyke crossing
a limestone layer. The limestone strikes N20degree E and dips 20degreeW.
The dyke strikes N15degreeW and dips 65degreeW. Find the orientation
and plunge of the ore body and its pitch on bothe vein and the bed .

20. solution

21. A set of homoclinal bed ids dipping 60 degree 048degree within which
the foreset laminae of cross bedding dips 40 degree 084degree. If the
original dip direction of foreset laminae give the direction of palaeocurrent,
findout original direction of palaeocurrent.

22. solution

23.  Lisle,R.J,and Leyshon,P.R (2004),Stereographic projection
Technique for Geologists ad Civil Engineers.(2nd edition)
Cambridge Publication.
 Jain .A.K (2014) ,an Introduction to Structural Geology( 1st
edition) Geological Society of india ,p.p 41-54
 Marshak .S. Mitra G(1985) , Basic method of Structural Geology,
prentice hall publication new jersey .p.p 87-192 .
 Roy ,A.K , (2009) ,Introduction to Geological Map and Structure,
3rd edition ,the world press private limited , p.p 149-173
 Fossen Haakon (2010),Structural Geology 1st year of
publication
REFERENCES

24. Conclusion
 In engineering geology project require stable slope ,which are dependent upon the
orientation of planer structure and their relation with angle and direction of slope .
 Invaluable tools in determining attitude of ancient paleodepositional bedding which
needed to established other significant geological data .
 It is helpful in plotting pi and β diagram hence guessing form of fold,
 We find many undersurface bedding , folding, faulting etc ,which could be analysed
by finding its attitude with the help of stereographic projection.
 We can plot many data in one place in any time and can find interrelated attitude,
so it is helpful in saving time and making many structural problem easy.