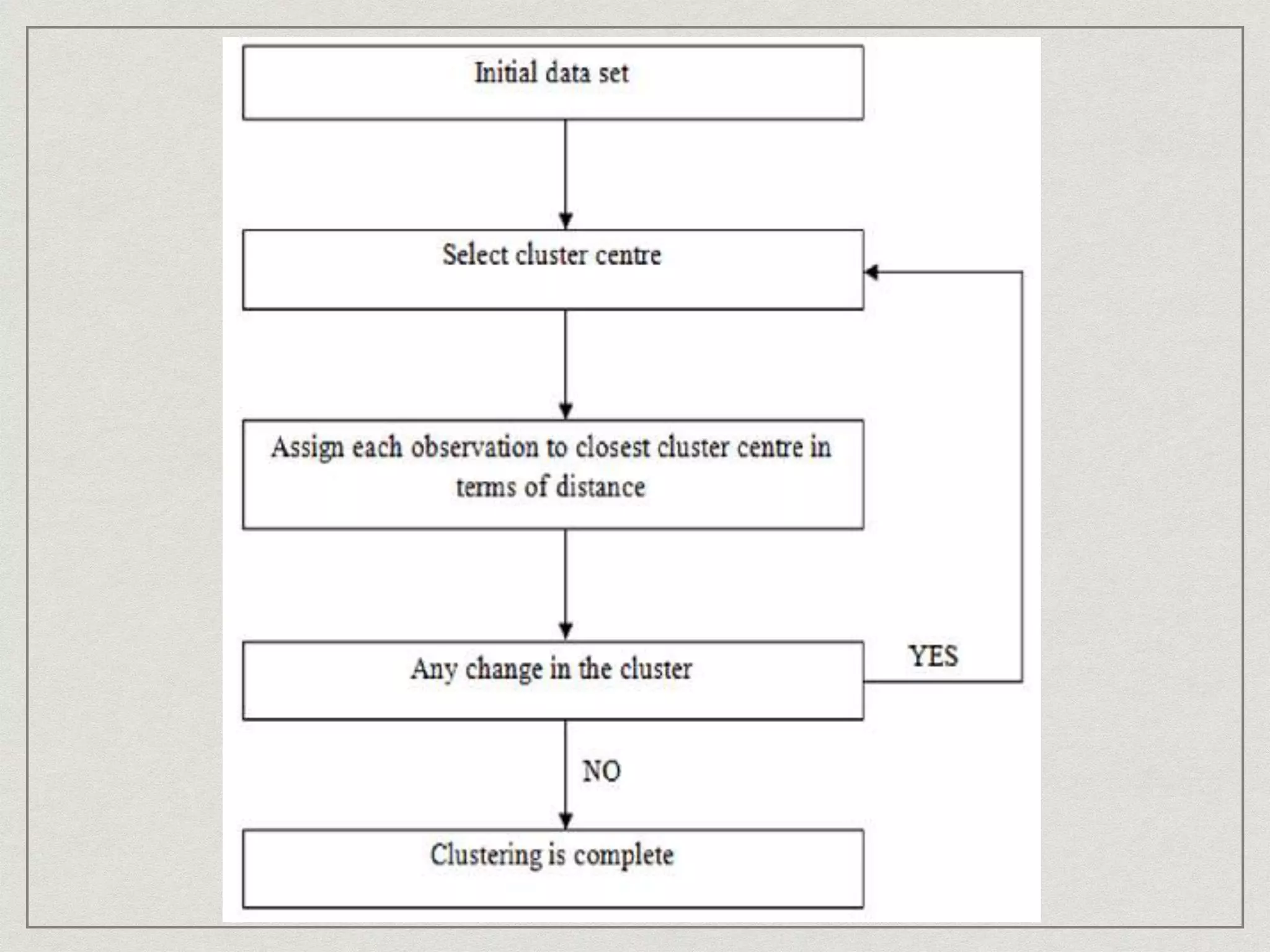
The document discusses the k-means algorithm used for clustering data points into 'k' clusters based on similarity measures, highlighting its dependence on the selection of initial centroids. It proposes an improved method for determining initial centroids to enhance clustering quality and reduce complexity through a two-phase process. The application of this improved algorithm includes rating-based clustering systems in e-commerce to optimize product organization and marketing strategies.

1. AMELIORATION OF
K-MEANS ALGORITHM

2. K-MEANS ALGORITHM

3. K-means algorithm is used for creating and
analyzing clusters.
In this algorithm, ‘n’ number of data points are
divided into ‘k’ clusters based on some similarity
measurement criterion.
However results generated using this algorithm are
mainly dependent on choosing initial cluster
centroids.

5. ADVANTAGES &
DISADVANTAGES

6. Advantages of k-means algorithm:
1. Ease of implementation and high-speed performance
2. Measurable and efficient in large data collection
Disadvantages of k-means algorithm:
1. Selection of optimal number of clusters is difficult
2. Selection of the initial centroids is random.

7. PROBLEM DEFINITION

8. •In the original k-means algorithm, the resulting
set of clusters strongly depends on the selection
of initial centroids which is random.
•Thus, in our project, we will propose a method
for calculating the initial centroids, which will
make the k-Means algorithm more efficient, so
as to get quality clustering with reduced
complexity.

9. PROPOSED SOLUTION

10. Phase-I: The input array of elements is scanned
and split up into sub-arrays, which represent the
initial clusters.
Phase-II: The centroids of previous initial clusters
are computed by calculating mean of each cluster.
Furthermore the data elements having less or equal
distance remains in the same cluster otherwise
they are moved to appropriate clusters. The entire
process continues until no changes in the clusters
are detected.

11. IMPROVED K-MEANS
ALGORITHM

12. Algorithm is divided into two Phases. In Phase-I, we find the initial
clusters, while in Phase-II, data elements are moved in appropriate
clusters.
Phase-I: To find the initial clusters
INPUT: Array {a1, a2, a3,..., an}
OUTPUT: A set of Initial Clusters.
Steps:
1) Find the size of cluster Si by calculating (n/k).
Where n= number of data points Dp (a1, a2, a3, ...... an)
k= number of clusters.
2) Create 'k' number of Arrays Ak
3) Move data points (Dp) from Input Array to Ak until Si.
4) Continue Step 3 until all Dp is removed from input array
5) Exit with having 'k' initial clusters.

13. Phase-II: To find the final clusters
INPUT: A set of Initial Clusters.
OUTPUT: A set of k Clusters.
Steps:
1) Compute the Arithmetic Mean M of all initial clusters C
2) Set 1≤ j≤ k
3) Compute the distance D of all Dp to M of Initial Clusters Cj
4) If D of Dp and M is less than or equal to other distances of Mi (1≤
i≤ k) then Dp stays in same cluster Else Dp having less D is assigned
to Corresponding Ci
5) For each cluster Cj (1≤ j≤ k), Recompute the M and move Dp until
no change in clusters.

14. APPLICATION

15. Rating based clustering system.
In E - commerce sites to cluster products based on
ratings to optimize the purchase-profit ratio of the
enterprise.
Useful for enhanced marketing and devising sales
strategy.

16. THANK YOU!