Downloaded 367 times
Uploaded byVanya Valindria
Radon Transform - image analysis
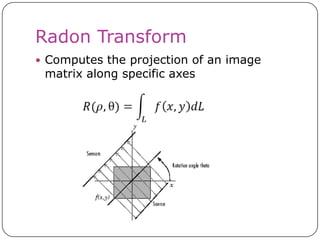
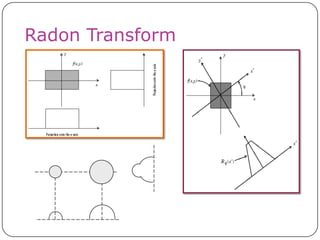
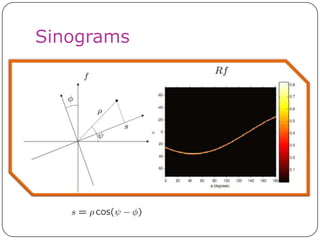
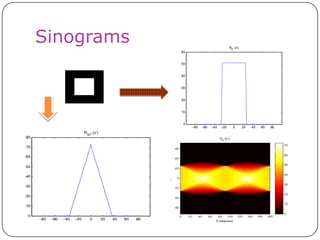
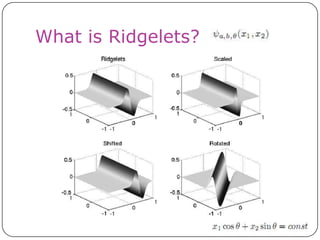
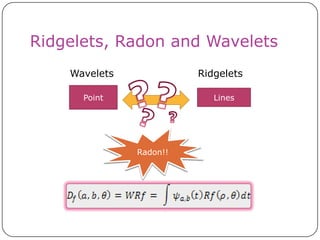
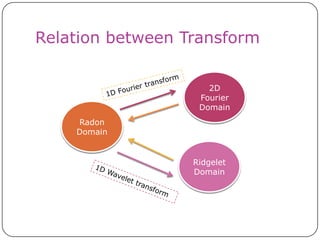
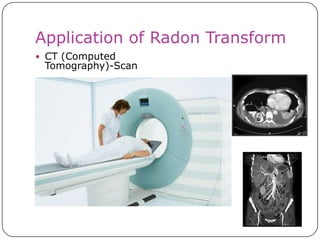
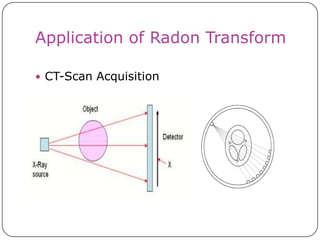
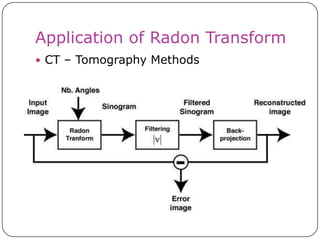
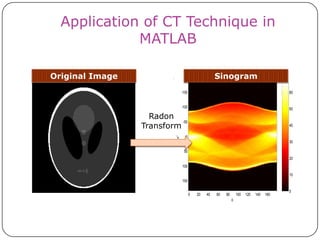
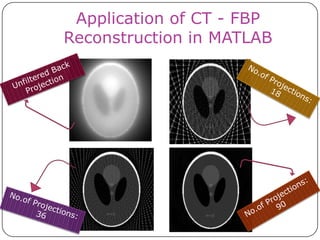
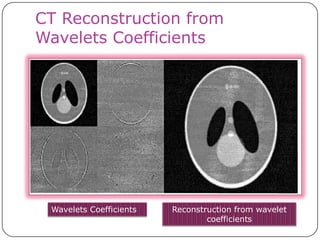
This document discusses the Radon transform and its applications in image processing. It introduces ridgelets as an extension of wavelets that are more effective for line and curve singularities. Ridgelets are derived from the Radon transform and wavelets. The Radon transform computes projections of an image along axes and is used in computed tomography (CT) scans to reconstruct tissue density images from X-ray measurements. Wavelets can localize the Radon transform for reconstruction. Ridgelets and the Radon transform have applications in tasks like line detection in images.
More Related Content
Similar to Radon Transform - image analysis
![11.[23 36]quadrature radon transform for smoother tomographic reconstruction](https://cdn.slidesharecdn.com/ss_thumbnails/11-23-36quadratureradontransformforsmoothertomographicreconstruction-120512235621-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
Radon Transform - image analysis
- 1. Radon Transform, Ridgeletsand their Applications in Image Processing Image Analysis Project By: Vanya V.Valindria Eng Wei Yong -VIBOT 4-
- 2. Outline Radon Transform Wavelets and Radon Transform Ridgelets Transform Applications in Image Processing
- 3. Radon Transform Computesthe projection of an image matrix along specific axes
- 4.
- 5.
- 6.
- 7. Wavelets and Radon In even dimension Radon Transform is not local Projection over all hyper planes is required for reconstruction of image In odd dimension only hyperplane that is in the neighborhood of x is required Less radiation exposed to patient is desired Hence, application of wavelet theory to RT
- 8. Wavelets and Radon The expansion of Radon using wavelets analysis: The wavelets coefficients can be used for Inverse Radon Transform
- 9. Why Ridgelets? Weaknessin wavelets only effective to adapt in point singularities A ridgelet is effective for higher dimensional singularities (line, curve, etc.) Next generation of wavelets
- 10.
- 11. Ridgelets and Wavelets ContinuousRidgelet Continuous Transform Wavelets Transform For a 2D Separable CWT Wavelet in 2D is the tensor product of: Line Point b, θ b1, b2
- 12. Ridgelets, Radon andWavelets Wavelets Ridgelets Point Lines Radon!!
- 13. Relation of Ridgeletswith Radon transform Original Image: f Radon Domain: Rf Radon Transform Ridgelets Domain: Df
- 14. Fourier Slice Theorem Links Radon and Fourier transform F-1 F (Rf) = F(u,v) f(x,y) Base for reconstruction
- 15. Relation between Transform 2D Fourier Domain Radon Domain Ridgelet Domain
- 16. Application of RadonTransform CT (Computed Tomography)-Scan
- 17. Application of RadonTransform CT-Scan Acquisition
- 18. Application of RadonTransform CT – Tomography Methods
- 19. Application of CTTechnique in MATLAB Original Image Sinogram -150 60 -100 50 Radon -50 Transform 40 0 x 30 50 20 100 10 150 0 0 20 40 60 80 100 120 140 160
- 20. Application of CT- FBP Reconstruction in MATLAB
- 21. CT Reconstruction from WaveletsCoefficients Wavelets Coefficients Reconstruction from wavelet coefficients
- 22. Application of RadonTransform
- 23. Application of Ridgelets Transform • Line Detection Original Image From wavelet From ridgelet component coefficients
- 24. Conclusion Radon transformis the key method for tomographic imaging Wavelets can be applied for Radon localization and inverse Radon transform Ridgelets can be derived from Radon and wavelets transform Radon transform and Ridgelets have wide applications in image processing
- 25. References Berenstein, C. Radon Transforms, Wavelets, and Applications. Technical Research Report: Engineering Research Center Program the University of Maryland. Hiriyannaiah, H. P. X-ray computed tomography for medical imaging. IEEE Signal Processing Magazine, March 1997: 42-58. Chen, G.Y. Image Denoising with Complex Ridgelets. 2007. Pattern Recognition 40, pp.578- 585. Carre, P., Andres.Eric. Discrete Analytical Ridgelet Transform. 2004. Signal Processing 84, pp.2165 – 2173. Toft, Peter. The Radon Transform: Theory and Implementation. Denmark: Technical University; 1996. Ph.D. Thesis. Farrokhi, F.R. Wavelet-Based Multiresolution Local Tomography. 2007. IEEE Transcations on Image Processing, Vol.6 No.10. Candes, E., Donoho, D.L.: Ridgelets: A Key to Higher-Dimensional Intermittency? .1999. Phil. Trans. R. Soc. Lond. A, 2495–2509. Zhao, S. Welland, G. Wavelet Sampling and Localization Schemes for the Radon Transform in Two Dimensions. 1997. Journal in Applied Mathematics, Vol.57, No.6 pp.1749 – 1762. Do MN, Vetterli M. The finite ridgelet transform for image representation. 2003. IEEE Transactions on Image Processing 1:16–28. Hasegawa,M. A Ridgelet Representation of Semantic Objects Using Watershed Segmentation. 2004. International Symposium on Communication and Information Technologies, Japan.
Editor's Notes
- #4 What is Radon Transform? It computes the projection of an image matrix along a specific axes. The image in two-dimension f(x,y) is projected into new axes which can be represent by and θ, where θ measures the counter-clockwise angle of the line from the horizontal axes, and measures the distance of the line from the origin of the (x,y) plane.A projection over a two-dimensional function f(x,y) is a set of line integral with each line (sum of the pixel along the line) separated by a specific width length. The multiple beam sources projected over different angle with respect to the centre of the object in order to represent an image.
- #5 3 different example of radon transform are showed. First a simple rectangle. If the image is projected to x-axes, which is the sum of the pixel along .., then image is like this.2nd example,For a square with projected at an angle theta from the x-axes. The maximum of the radon tranform is along the diagonal of the square as the sum of the pixel is max along this line & decreasing as the line integral go away from the diagonal line as line integral decrease. 3rd example,Show a Radon transform when projected to x & y axes. The max is at the centre of the circle & decrease as the go away from the centre.
- #6 Now, we look at the radon transform of a single point onto an axes defined by role and fife, we compute the projection of the point using the formula as shown. and we do it from 0 to 180 degree, the radon transform wil trace out as a sinusoidal function as shown in the diagram. And this is what we called sinograms.
- #7 If we compute the radon transform for this image at 0 degree, this is what we get. While at 45 degree, the radon transform turns out to be the triangle shape as shown as the max over the diagonal line and gradually decrease as it go away from the diagonal line. And, if we do the radon tranform from 0 to 180 degree for this image, the results turns out to be a sinugrams as much complex than the radon transform of a single point in previous slide.
- #8 It is well known that the Radon transform is not localized in two dimensions or even number dimension. Hence, the recovery of f(x) in even dimension requires the integral of f over all hyper planes. In contrary, recovery in odd dimension that only the integral of f over hyper planes that pass through neighborhoods of x is required. That means in even dimension, the recovery of an image at any point requires the information of all projection of image. For tomography example, the patient has to expose to huge amount of X-Ray even though only small part of the patient body is desired to observe in the process. It is desired that the patient is exposed to as little radiation as possible. In order to acquire complete reconstruction of the ROI (Region of Interest) and reduce amount of radiation (in CT), the application of the wavelet theory to the inversion of the Radon Transform was proposed [6].
- #9 The formula for direct inversion Rθf(s) for each angle θ is:The inverse radon transform using wavelet function are local in both odd & even dimension, hence solve the problem of localization in even dimension & reduce the amount of radiation required to expose to the patient. Selective recovery of f at certain resolution. Remove noise in tomographic images.
- #10 The success of wavelets is mainly due to the good performance at catching zero-dimensional or point singularities, but two-dimensional like images have one-dimensional singularities, such asedges, whichare typically smooth curves. Intuitively, wavelets in two dimensions are obtained by a tensor-product of one dimensional wavelets and they are thus good at detecting the discontinuity across an edge, but will not see the smoothness along the edge.To overcome the weakness of wavelets in higher dimensions, Candes and Donoho proposed theridgelets which deal effectively with line singularities in 2-D.
- #11 This is ridgelet function, which is oriented at an angle and is constant along the line…This ridgelet can be scaled, translated and rotated.
- #12 If we compare ridgelets and wavelets..In continous domain, the CRT is deifned by… whereas the rigdelets is this:As can bee seen, this ridgelets transform is similar to the 2D continuous wavelets transform except that the point parameter translation in b1 and b2 are replaced by the line parameter.As a consequence, wavelets are very effective in representing objects with isolated point singularities, while ridgelets are very efiective in representing objects with singularities along lines, edges, etc.
- #13 How to link these point and lines? What is the link between ridgelets and wavelets??We should recall that, In 2-D, points and lines are related via the Radon transform.Thus the wavelet and ridgelet transforms are linked via the Radon transform…!!Then, the ridgelet transform is the application of a wavelet transform to the slice of the Radon transform
- #14 As an illustration, if we convert the original image (Figure 6-top) by Radon transform, we can get a sinogram in Radon domain (Figure 6-bottom left). Then, each column (in red) on the Radon domain is converted by the 1-D wavelet transform. Finally, we can get the result of Ridgelet domain
- #15 One of the important properties of the Radon transform is its relationship to the Fourier transform called Fourier Slice Theorem.If we calculate the Fourier transform of our Radon transform of an image for all angles then it is the same as the Fourier transform of the image. Thus, we can easily obtain the original image by taking the inverse Fourier transform of that.
- #16 Ridgelets analysis can be constructed as wavelet analysis in the Radon domain. Meanwhile, by applying the 1-D inverse Fourier transform to the 2-D Fourier transform from radial lines to origin, we can obtain the Radon transform
- #17 Radon transform is the basis for tomographic imaging technique that allows examining slices of the human body without damaging it. Commonly Radon transform is applied in computed tomography (CT) in medical field.
- #18 A CT-scanner consists of a ring with one X-ray emitter and many detectors in the opposite side to the emitter as shown in Figure. Here, the beams of radiation are passed through the body being imaged from various positions and angles.After the scan, the attenuation maps can be found by reconstruction using inverse Radon transform.
- #19 A brief explanation of step-by-step methods in CT technique is described as the following:Radon transform :In each rotation, the body is X-rayed from several angles to produce the sinogram using the Radon transform. Filtered Back projection (FBP):This algorithm approximates the image based on the projection obtained in the acquisition. Filtering :To compensate the blur introduced when summing up the backprojections of all sinogram lines. Backprojection:Thebackprojection operator is integration along a sine-curve in the filtered sinogram [5].
- #20 Supposed we have a phantom image of the brain (Figure 9 left). We can compute the Radon transform with specified number of projections. Figure 9-right displays a plot of the Random transform or the corresponding sinogram using 90 projections from 0 to 180 degrees. First column in this Radon transform correspond to a projection at 0 degrees
- #21 Next, we can reconstruct the original image from the projection data using Inverse Radon with Filtered Back Projection method. In Figure 10a, we can see that if we used unfiltered back-projection, the result is blur and noisy. After we applied Ram-Lak filter in FBP, the image reconstruction gives a better quality. Figure 10b and 10c shows that using a less number (18 and 36) of projections can lead to inaccurate reconstruction images and include some artifacts from the back-projection. Meanwhile, using more (90) projections the reconstruction (Figure 10d) resembles to the original image. The results above explained that according to the projection-slice theorem, if we have an infinite number of projections of the object taken at infinite number of orientation, we can reconstruct the original object perfectly by finding the inverse Radon transform [5].
- #22 Instead of using FBP for reconstruct image, there is also an algorithm to reconstruct the image by taking the wavelet coefficients from the Radon transform data first. Here, wee can see the approximation and detail, to be used in multi-resolution reconstruction formulas. Then, the quality of the reconstructed image is the same as with the FBP method. This algorithm have advantages, such as more effieicent in computation and more localized.
- #24 Figure 13 shows the original image contains only lines and isotropic Gaussians. The middle image is the reconstructed component from the wavelets component. Whereas, the reconstructed layer from the ridgelets coefficients (right) gives clear separated line component