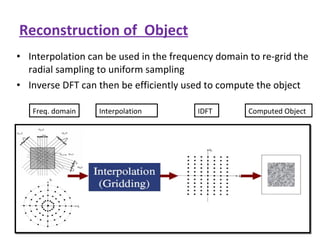
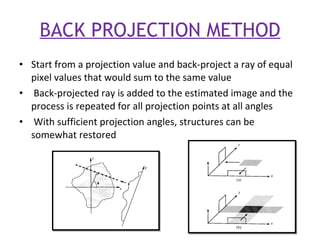
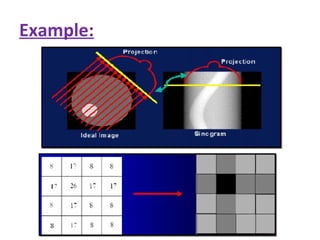
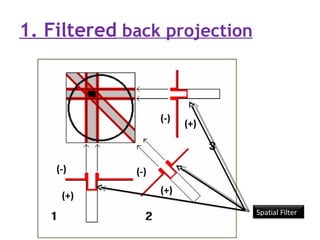
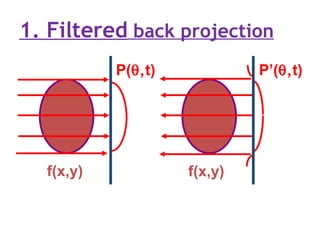
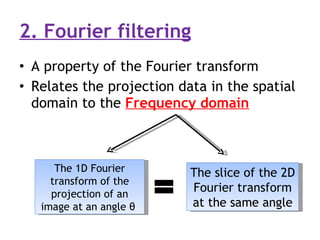
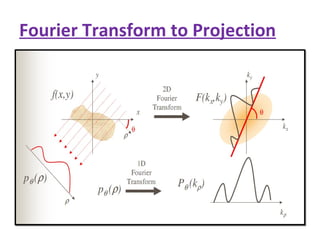
1. Computed tomography (CT) image reconstruction involves estimating digital images from measured x-ray projection data. Early methods included back projection, which was simple but produced blurred images. 2. Modern commercial CT scanners use analytical methods like filtered back projection or Fourier filtering to reduce blurring. These methods apply spatial or frequency domain filters to projection data before back projecting to reconstruct the image. 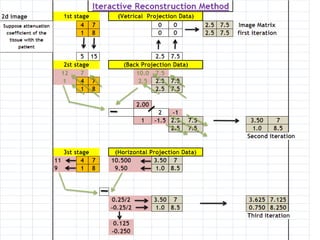3. Iterative reconstruction methods were also developed and provide better image quality than analytical methods but are too computationally intensive for clinical use. Current research aims to make iterative methods fast enough for real-time medical imaging.

1. COMPUTED TOMOGRAPHY IMAGE RECONSTRUCTION Presented By: Gunjan Patel (MS-Medical Software ) (B.E.-Biomedical Engg.) (PGQ-Quality Management)

2. History of Image Reconstruction 1917 Radon has developed mathematical solution to the problems of image reconstruction from of a set of projection . Utilization in solving problems in astronomy and optics. 1961 finally these techniques were used in medical field .

3. CT Image Reconstruction For an N×N image, we have N unknowns to estimate the digital image reconstruction. 2 pixel

4. IMAGE RECONSTRUCTION

5. BACK PROJECTION METHOD The oldest method Not used in commercial ct scanners Method is analogous to a graphic reconstruction Processing part is simple and direct Each projection can not contribute originally formal of profile Some produces images are ‘Starred’ and ‘blurring’ that makes unsuitable for medical diagnosis A sinogram is a special x-ray procedure that is done with contrast media (x-ray dye) to visualize any abnormal opening (sinus) in the body

6. BACK PROJECTION METHOD Start from a projection value and back-project a ray of equal pixel values that would sum to the same value Back-projected ray is added to the estimated image and the process is repeated for all projection points at all angles With sufficient projection angles, structures can be somewhat restored

7. Example:

8. Problem: Problems with back-projection include mainly severe blurring in the computed images

9. Iterative reconstruction Successive approximation method Iterative least squares techniques Algebraic reconstruction Hounsfield used this technique in his First EMI BRAIN SCANNER Iterative methods are not use in today commercial scanners

10. Example: Successive approximation method to obtain an image of attenuation coefficients from the measured intensity form Object slice The attenuation coefficient of the object are unknown before hand Calculation of Method: Click

12. Analytical methods Current Commercial scanner uses this method A mathematical technique known as convolution or filtering Technique employs a spatial filter for remove blurring artifacts. 2 types of method Filtered back projection Fourier filtering

13. 1. Filtered back projection (-) (-) (-) (+) (+) (+) Spatial Filter

14. 1. Filtered back projection This technique elimination the unwanted cusp like tails of the projection. The projection data are convoluted with suitable processing function before back projection The filter function has negative side lobes surrounding a positive core , so that in summing the filtered back projection - positive and negative contribution that cancel outside the central core  The constructed image resemble Original object

15. 1. Filtered back projection f(x,y) f(x,y) P(  t) P’(  t)

16. 2. Fourier filtering A property of the Fourier transform Relates the projection data in the spatial domain to the Frequency domain The 1D Fourier transform of the projection of an image at an angle θ The slice of the 2D Fourier transform at the same angle

17. Fourier Transform to Projection

18. Fourier Slice Theorem Ky Kx  F(Kx,Ky) F[P(  t)] P(  t) f(x,y) t  y x X-rays

19. Mathematical Illustration 2D Fourier transformation: The slice of the 2D Fourier transform at kx=0 is given by: and at ky=0 is given by

20. From Projections to Image y x Ky Kx F -1 [F(Kx,ky)] f(x,y) P(  t) F(Kx,Ky)

21. Reconstruction of Object Interpolation can be used in the frequency domain to re-grid the radial sampling to uniform sampling Inverse DFT can then be efficiently used to compute the object Freq. domain Interpolation IDFT Computed Object

22. References http://www.slideshare.net/NYCCT1199/ct-reconstruction-methods http://en.wikipedia.org/wiki/Iterative_reconstruction Handbook of Biomedical Instrumentation-R.S.Khandpur

23. Queries !!!