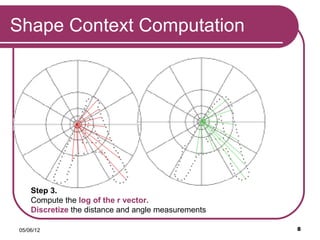
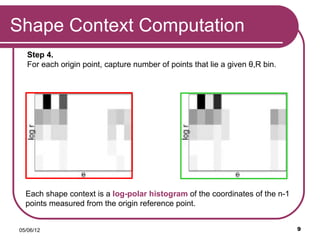
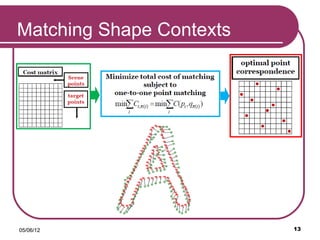
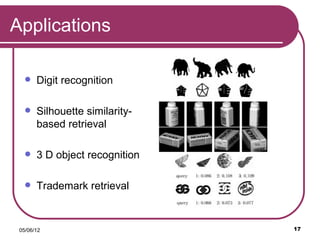
The document discusses the Shape Context method for measuring similarities between shapes, focusing on its algorithm for object classification and recognition. It outlines the process stages, computation steps, and applications such as digit recognition and silhouette retrieval. The method is noted for its invariance to translation, scale, and rotation, making it a valuable tool for shape matching.

1. Shape Context
Rocío Cabrera u1908272
Vanya Valindria u1908259
06/05/12 1

2. Introduction
Can you guess what number it is?
05/06/12 2

3. Objectives
“Have descriptors that can be computed in
one image and used to find corresponding
points, if visible, in another image.”
“Given a query model image, to develop an
algorithm capable of retrieving similar-
shaped images from an extensive database”
05/06/12 3

4. Process Stages
Solve the Use the
Evaluate the
correspondences Compute the
correspondence
.
problem between
the two shapes
.
to estimate an
aligning
transform
distance between
the two shapes ?
distance and
classify the
shape
05/06/12 4

5. SHAPE CONTEXT
“A novel approach to measuring similarities between shapes and
exploit it for object classification/recognition”
05/06/12 5

6. Shape Context Computation
Step 1.
Obtain from ShapeP and ShapeQ n-samples uniformly spaced taken from
their edge elements
05/06/12 6

7. Shape Context Computation
Step 2.
Compute the Euclidean distance (r) and the angle (θ) from each point in
the set to all the other n-1 points.
Normalize r by the median distance (λ) and measure the angle relative to
the positive x-axis.
05/06/12 7

8. Shape Context Computation
Step 3.
Compute the log of the r vector.
Discretize the distance and angle measurements
05/06/12 8

9. Shape Context Computation
Step 4.
For each origin point, capture number of points that lie a given θ,R bin.
Each shape context is a log-polar histogram of the coordinates of the n-1
points measured from the origin reference point.
05/06/12 9

10. Shape Context Computation
 Shape context of the sample points in ShapeP and
ShapeQ.
05/06/12 10

11. Matching Shape Contexts
 How can we assign the sample points of ShapeP to
correspond to those of ShapeQ?
 Determining shape correspondences such that:
l Corresponding points have very similar descriptors
l The correspondences are unique
05/06/12 11

12. Matching Shape Contexts
 Define matching cost function
 Shape context
 Distance between the two normalized histograms
 Local appearance
 Dissimilarity of the tangent angles
05/06/12 12

13. Matching Shape Contexts
05/06/12 13

14. Modeling Transformation
 Given a set of correspondences, estimate a
transformation that maps the model into the target
 Euclidean transformation
 Affine model
 Thin Plate Spline (TPS)
05/06/12 14

15. Classification/Recognition
 This enables a measure of shape similarity
 The dissimilarity between two shapes can be computed
as the sum of matching errors between corresponding
points, together with a term measuring the magnitude
of the aligning transform
 Given a dissimilarity measure, a k-NN technique can
be used for object classification/recognition
05/06/12 15

16. Method Evaluation
Advantages Drawbacks
 Incorporates invariance to:  Sensitive local distortion or
blurred edges
 Translation
 Problems in cluttered
 Scale background
 Rotation
 Occlusions
05/06/12 16

17. Applications
 Digit recognition
 Silhouette similarity-
based retrieval
 3 D object recognition
 Trademark retrieval
05/06/12 17

18. Database for Digit Recognition
 MNIST datasets of
handwritten digits:
 60,000 training and
10,000 test digits
Links:
http://yann.lecun.com/exdb/mnist/
05/06/12 18

19. Database for Silhouette
 MPEG-7 shape silhouette
database (Core Experiment
CE-Shape-1 part B)
 1400 images: 70 shapes
categories and 20 images per
category
 Links:
http://mpeg.chiariglione.org/standards/mpeg-7/mpeg-7.htm
05/06/12 19

20. Database for 3-D object recognition
 COIL-20 database
 20 common household
objects; turned every 5˚ for
a total of 72 views per
object
 Links:
http://www1.cs.columbia.edu/CAVE/software/softlib/coil-20.php
05/06/12 20

21. Database for Trademark retrieval
 300 different real-
world trademark
05/06/12 21

22. MATLAB DEMO
05/06/12 22

23. Conclusions
 The shape context method is simple to implement
yet it is a rich shape descriptor
 The methodology makes it invariant to translation,
scale and rotation
 Useful tool for shape matching and recognition
05/06/12 23