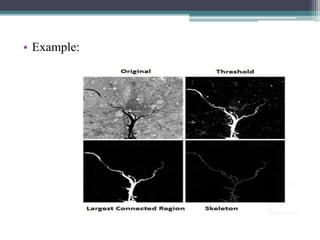
This document discusses topological features in digital images. It defines digital topology as dealing with the topological properties of digital images, providing a mathematical basis for image processing operations. It describes several topological descriptors that are invariant to deformations, including the number of holes (H), number of connected components (C), and Euler number (E=C-H). These descriptors can be used to characterize shapes and regions in images.

1. TOPOLOGICAL FEATURES
R.PAVITHRA
II-MSc-(IT)
DEPARTMENT OF CS&IT
NADAR SARASWATHI COLLEGE OF ARTS AND SCIENCE
THENI.

2. TOPOLOGICAL FEATURES
Digital topology deals with the topological
properties of digital image and provides a sound
mathematical basis for image processing operations
such as image thinning, border following and
connected component labeling. Matrix structure is also
a consistent mathematical framework for image
processing.

3. TOPOLOGICAL DESCRIPTORS
Topology refers to properties of the shape that
don't change, so long as you aren't allowed to tear
or join parts of the shape. (You should know how
to use connected-component labeling to
determine the Euler number.)

4. Cont..
• Topology is the study of properties a figure that are
unaffected by any deformation, as long as there is no
tearing or joining of the figure(also called rubber-
sheet distortions).
• Number of holes in region H.
• Number of connected components C.
• Euler number E=C-H.

5. Cont…
• Number of holes(H):
▫ Invariants to several operators.

6. Cont..
• Number of connected components(C):
▫ Invariants to several operators.

7. Cont…
• Euler number(E=C-H):
▫ Invariants to several components

8. Cont…
• Polygonal net:
▫ V:#of vertices(7)
▫ Q:# of edges(11)
▫ F:# of faces(2)
▫ E=C-H=V-Q+F
 C=1,H=3
 E=-2

9. • Example:

10. T
H
A
N
K
Y
O
U