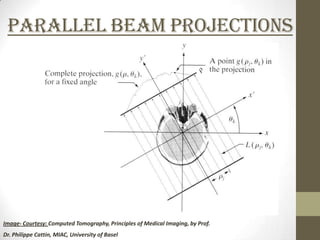
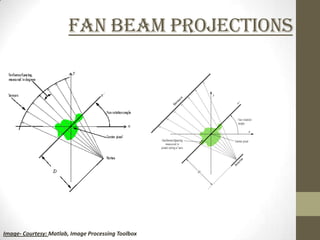
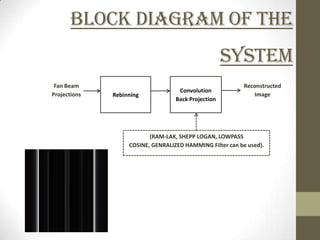
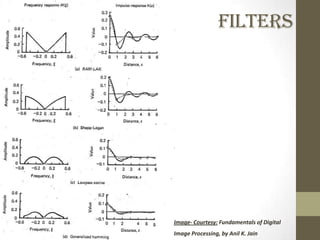
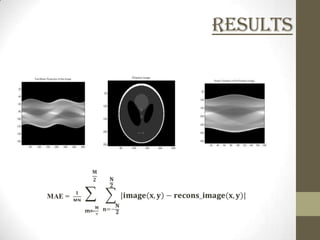
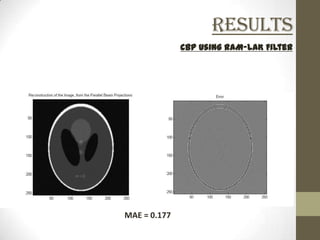
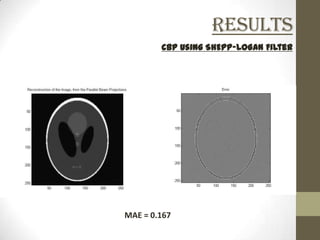
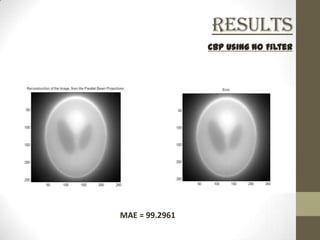
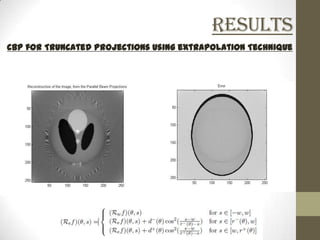
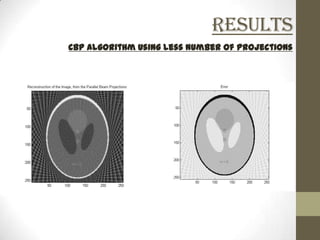
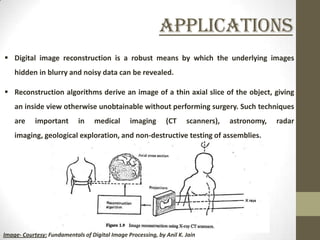
This document discusses two-dimensional image reconstruction algorithms. It begins with an introduction to image projections and reconstruction. It then describes different types of projections like parallel beam, fan beam, and truncated projections. It discusses the convolution back projection algorithm and its digital implementation. Results are shown for different filters. Applications include medical imaging. Present research focuses on limited data reconstruction. The document concludes that image reconstruction is an ill-posed problem.

1. Two Dimensional Image
Reconstruction Algorithms
-By,
Srihari K. Malagi,
Reg No. 090907471
Roll No. 53
Section A
Dept. of Electronics & Communication
Manipal Institute of Technology.
Image Courtesy: Advanced Electron Microscopy Techniques on Semiconductor Nanowires: from Atomic Density of States Analysis to 3D Reconstruction
Models, by Sonia Conesa-Boj, Sonia Estrade, Josep M. Rebled, Joan D. Prades, A. Cirera, Joan R. Morante, Francesca Peiro and Jordi Arbiol

2. Data Flow
 Introduction
 Parallel Beam Projections
 Fan Beam Projections
 Truncated Projections
 Convolution Back-Projection Algorithm
 Digital Implementation
 Results
 Applications
 Present Research
 Conclusion
 References

3. Introduction
 What are Projections?
 How to obtain Projections?
 What is Image Reconstruction?
 What are Truncated Projections?
Image- Courtesy: Fundamentals of Digital Image Processing, by Anil K. Jain

4. Parallel Beam Projections
Image- Courtesy: Computed Tomography, Principles of Medical Imaging, by Prof.
Dr. Philippe Cattin, MIAC, University of Basel

5. Fan Beam Projections
Image- Courtesy: Matlab, Image Processing Toolbox

6. Radon Transform
Image- Courtesy: Matlab, Image Processing Toolbox

7. Inverse Radon Transform
For reconstruction of the image, we define Inverse Radon Transform
(IRT) which helps us achieve in defining the image from its projection data.
Inverse Radon Transform is defined as:
f(x,y) =

8. Reconstruction of an
Image: Algorithm

9. Rebinning
Fan Beam Projections can be related to parallel beam projection data as:
s = Dsinα ; θ = α + β;
Therefore,
g(s,θ) = b(sin-1 s/D, θ - sin-1 s/D);
Hence to obtain g(sm,θm) we interpolate b(α,β).
This process is called Rebinning.

10. Block Diagram of the
System
Fan Beam Reconstructed
Convolution
Projections Rebinning Image
Back Projection
(RAM-LAK, SHEPP LOGAN, LOWPASS
COSINE, GENRALIZED HAMMING Filter can be used).

11. Filters
Image- Courtesy: Fundamentals of Digital
Image Processing, by Anil K. Jain

12. Results

13. Results
CBP using RAM-LAK Filter
MAE = 0.177

14. Results
CBP using SHEPP-LOGAN Filter
MAE = 0.167

15. Results
CBP using No Filter
MAE = 99.2961

16. Results
CBP for Truncated Projections (wrt s)

17. Results
CBP for Truncated Projections using extrapolation Technique

18. Results
CBP algorithm using less number of projections

19. Applications
 Digital image reconstruction is a robust means by which the underlying images
hidden in blurry and noisy data can be revealed.
 Reconstruction algorithms derive an image of a thin axial slice of the object, giving
an inside view otherwise unobtainable without performing surgery. Such techniques
are important in medical imaging (CT scanners), astronomy, radar
imaging, geological exploration, and non-destructive testing of assemblies.
Image- Courtesy: Fundamentals of Digital Image Processing, by Anil K. Jain

20. Present Research
Presently, the key concern is on Reconstruction of objects using
limited data such as truncated projections, limited projections etc… Filtered
Back-projection (FBP) Algorithms have been implemented since the system is
faster when compared to CBP Algorithm. Also new techniques such as
Discrete Radon Transform (DRT) Techniques have been implemented to
achieve the goal.
Also Fan Beam projections are considered for 2D image
reconstructions, since less number of projections will be required when
compared to parallel beam projections. Also from the conventional fixed focal
length Fan-Beam projections, we have observed that the research is moved
onto defining variable focal length Fan-Beam Projections.

21. Conclusion
Image reconstruction is unfortunately an ill-posed problem.
Mathematicians consider a problem to be well posed if its solution (a)
exists, (b) is unique, and (c) is continuous under infinitesimal changes of the
input. The problem is ill posed if it violates any of the three conditions.
In image reconstruction, the main challenge is to prevent
measurement errors in the input data from being amplified to unacceptable
artifacts in the reconstructed image.
“New techniques are being implemented, and tested to overcome
these problems.”

22. References
 Soumekh, M., IEEE Transactions on Acoustics, Speech and Signal
Processing, Image reconstruction techniques in tomographic imaging
systems, Aug 1986, ISSN : 0096-3518.
 Matej, S., Bajla, I., Alliney, S., IEEE Transactions on Medical Imaging, On
the possibility of direct Fourier reconstruction from divergent-beam
projections, Jun 1993, ISSN : 0278-0062.
 You, J., Liang, Z., Zeng, G.L., IEEE Transactions on Medical Imaging, A
unified reconstruction framework for both parallel-beam and variable
focal-length fan-beam collimators by a Cormack-type inversion of
exponential Radon transform, Jan. 1999, ISBN: 0278-0062.

23. References
 Clackdoyle, R., Noo, F., Junyu Guo., Roberts, J.A., IEEE Transactions on
Nuclear Science, Quantitative reconstruction from truncated projections in
classical tomography, Oct. 2004, ISSN : 0018-9499.
 O'Connor, Y.Z., Fessler, J.A., IEEE Transactions on Medical Imaging, Fourier-
based forward and back-projectors in iterative fan-beam tomographic
image reconstruction, May 2006, ISSN : 0278-0062.
 Wang, L., IEEE Transactions on Computers, Cross-Section Reconstruction
with a Fan-Beam Scanning Geometry, March 1977, ISSN : 0018-9340.

24. References
 Anil K. Jain, Fundamentals of Digital Image Processing, Prentice
Hall, Englewood Cliffs, NJ 07632, ISBN 0-13-336165-9.
 Avinash C. Kak and Malcolm Slaney, Principles of Computerized
Tomographic Imaging, Society for Industrial and Applied
Mathematics, Philadelphia, ISBN 0-89871-494-X.
 G. Van Gompel, Department of Physics, University of
Antwerp, Antwerp, Towards accurate image reconstruction from truncated
X-ray CT projections, Publication Type: Thesis, 2009.