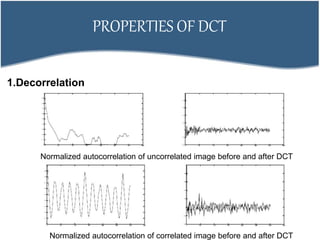
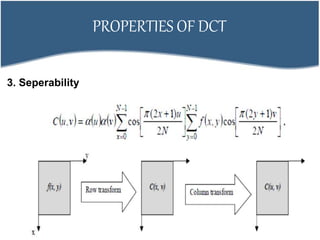
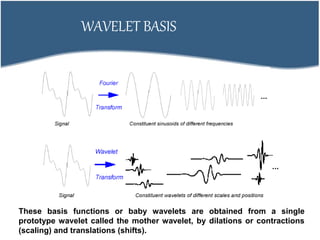
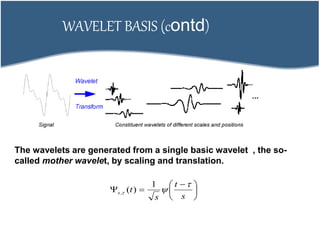
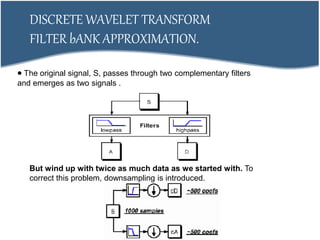
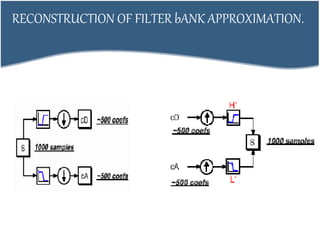
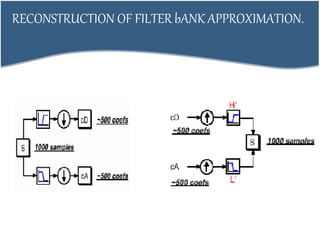
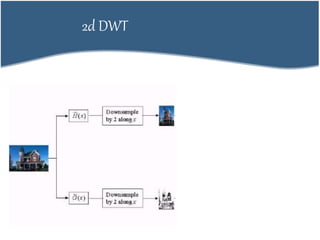
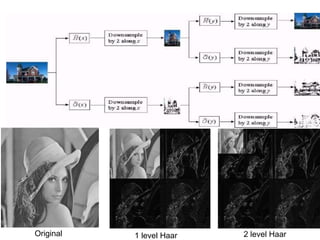
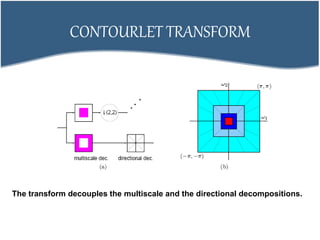
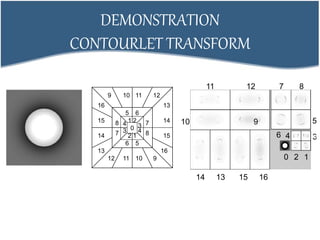
1. The document discusses various image transforms including discrete cosine transform (DCT), discrete wavelet transform (DWT), and contourlet transform. 2. DCT transforms an image into frequency domain and organizes values based on human visual system importance. DWT analyzes images using wavelets of different scales and positions. 3. Contourlet transform is derived directly from discrete domain to capture smooth contours and edges at any orientation, decoupling multiscale and directional decompositions. It provides better efficiency than DWT for representing images.

1. IMAGE TRANSFORMS.
MAHESH MOHAN.M.R
GECT S3 ECE
ROLL NO: 5
OM NAMA
SIVAYA
SHIVA KUDE KANANE…

2. DISCRETE COSINE TRANSFORM







1
0
1
0
),(
2
)12(
cos
2
)12(
cos
)()(2
),(
M
i
N
j
jif
N
vj
M
ui
MN
vCuC
vuF

Given a function f(i, j) over two integer variables i and j, the
2D DCT transforms it into a new function F(u, v), with integers u and
v running over the same range as i and j such that
where i,u = 0, ..., M – 1 and j,v = 0, ..., N – 1
and







otherwise
xif
xC
1
0
2
1
)(

3. SIGNIFICANCE OF DCT
The entries in Y will be organized based on the human visual system.
The most important values to our eyes will be placed in the upper left corner
of the matrix.
The least important values will be mostly in the lower right corner of the
matrix.
Horizontal freq
Most
Important
Verticalfreq
Semi-
Important
Least
Important
DCT MATRIX

4. DEMONSTRATION OF DCT
Can You Tell the Difference?
ORIGINAL Base layer (MSE =38.806)
DCT MATRIX

5. PROPERTIES OF DCT
1.Decorrelation
Normalized autocorrelation of uncorrelated image before and after DCT
Normalized autocorrelation of correlated image before and after DCT

6. PROPERTIES OF DCT
2. Energy Compaction
GECT and its DCT

7. PROPERTIES OF DCT
3. Seperability

8. A serious drawback in transforming to the
frequency domain, time information is lost.
When looking at a Fourier transform of a signal,
it is impossible to tell when a particular event
took place.
DRAWBACK OF DCT

9. HISTORY OF WAVELET
1805 Fourier analysis developed
1965 Fast Fourier Transform (FFT) algorithm
1980’s beginnings of wavelets in physics, vision, speech processing
1986 Mallat unified the above work
1985 Morlet & Grossman continuous wavelet transform …asking: how can
you get perfect reconstruction without redundancy?
1985 Meyer tried to prove that no orthogonal wavelet other than Haar
exists, found one by trial and error!
1987 Mallat developed multiresolution theory, DWT, wavelet construction
techniques (but still noncompact)
1988 Daubechies added theory: found compact, orthogonal wavelets with
arbitrary number of vanishing moments!
1990’s: wavelets took off, attracting both theoreticians and
engineers

10. • For many applications, you want to analyze a
function in both space and frequency
• Analogous to a musical score
WHY WAVELET TRANSFORM
Discrete transforms give you frequency information, smearing
space.
Samples of a function give you temporal information,
smearing frequency.

11. These basis functions or baby wavelets are obtained from a single
prototype wavelet called the mother wavelet, by dilations or contractions
(scaling) and translations (shifts).
WAVELET BASIS

12. WAVELET BASIS (contd)
The wavelets are generated from a single basic wavelet , the so-
called mother wavelet, by scaling and translation.





 

s
t
s
ts


1
)(,

13. DISCRETE WAVELET TRANSFORM
 Discrete wavelet is written as





 
 j
j
j
kj
s
skt
s
t
0
00
0
,
1
)(


j and k are integers and s0 > 1 is a fixed scaling step. The translation factor 0
depends on the scaling step. The effect of discretizing the wavelet is that the
time-scale space is now sampled at discrete intervals.
 



0
1
)()( *
,, dttt nmkj 
If j=m and k=n
others

14. DISCRETE WAVELET TRANSFORM
FILTER bANK APPROXIMATION.

15. But wind up with twice as much data as we started with. To
correct this problem, downsampling is introduced.
DISCRETE WAVELET TRANSFORM
FILTER bANK APPROXIMATION.
 The original signal, S, passes through two complementary filters
and emerges as two signals .

16. PRACTICAL EXAMPLE OF FILTER bANK APPROXIMATION.

17. RECONSTRUCTION OF FILTER bANK APPROXIMATION.

18. RECONSTRUCTION OF FILTER bANK APPROXIMATION.

19. Wavelet Decomposition
Multiple-Level Decomposition
The decomposition process can be iterated, so that one signal is broken
down into many lower-resolution components. This is called the wavelet
decomposition tree.

20. 2d DWT

21. Shiva kathone,,,,kude kannane
1 level Haar 2 level HaarOriginal

22. NEED FOR A NEW TRANSFORM?
Efficiency of a representation refers to the ability to capture significant
information about an object of interest using a small description.
Wavelet Curvelet

23. WHAT WE WISH
in ATRANSFORM?
Multiresolution. The representation should allow images to be successively
approximated, from coarse to fine resolutions.
Localization. The basis elements in the representation should be localized in
both the spatial and the frequency domains.
Critical sampling. For some applications (e.g., compression), the representation
should form a basis, or a frame with small redundancy.
Directionality. The representation should contain basis elements oriented at a
variety of directions
Anisotropy. To capture smooth contours in images, the representation should
contain basis elements using a variety of elongated shapes with different aspect
ratios.

24. CONTOURLET TRANSFORM
• Captures smooth contours and edges at any
orientation
• Filters noise.
• Derived directly from discrete domain
instead of extending from continuous
domain.
• Can be implemented using filter banks.

25. CONTOURLET TRANSFORM
The transform decouples the multiscale and the directional decompositions.

26. 4
DEMONSTRATION
CONTOURLET TRANSFORM
0
1
1
2
2
3
3 4
5
5
6
6
7
7 8
8
16
9
9
10
10
11
11
12
12
13
13
14
1415
15
16
10
0 12
34
5
6
7 8
15 161314
11 12
9 5
4

27. Shiva kathone,,,,kude kannane
Koode kaanane
Om nama sivaya
Koode kanane shiva