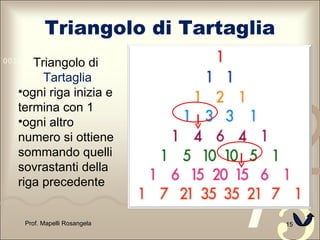
Il documento, redatto da Rosangela Mapelli, fornisce una panoramica sulle proprietà algebriche come il quadrato e il cubo di binomi, la somma per la differenza di binomi, e il quadrato di trinomio, con esempi pratici e esercizi. Viene anche menzionato il triangolo di Tartaglia, attribuendo una breve biografia a Niccolò Tartaglia, un matematico italiano noto per i suoi contributi nel campo dell'algebra. È inoltre sottolineata la licenza Creative Commons che permette la condivisione e modifica delle slide a patto di rispettare alcune condizioni.

1. Creato da Rosangela Mapelli Licenza Creative Commons Sei libero di modificare e pubblicare queste slide a patto di indicare l'autore, non trarne guadagno e devi condividere tutto ciò che ne deriva sotto la stessa licenza.

2. Prodotti Notevoli Quadrato del binomio Cubo del binomio Somma per la differenza di un binomio Potenza di un binomio Quadrato del trinomio Prof. Mapelli Rosangela

3. Somma per la differenza di un binomio Prof. Mapelli Rosangela Il prodotto della somma di due termini per la loro differenza è uguale al quadrato del primo termine meno il quadrato del secondo termine

4. ESEMPI: Prof. Mapelli Rosangela (3a + 2b)(3a - 2b) = 9a 2 - 4b 2 ( - a - 3b)( - a + 3b) = a 2 - 9b 2 ( - 4a + 2b)( - 4a + 2b) = 4b 2 - 16a 2 (a - 3b + c)(a + 3b - c) = [a - (3b - c)][a + (3b - c)] = [a 2 - (3b - c) 2

5. Somma per differenza: esercizi (2a + 7)(2a - 7)= (3a - 4b)(3a+ 4b) = (-2x - 3y)(-2x+3y) = (a 2 + 3b)(a 2 - 3b) = (5a - 3b)(5a+ 3b) = (5a 2 +2b 2 )(5a 2 -2b 2 ) = (-3a 3 +2b 2 )(-3a 3 -2b 2 ) = (2a + 3b)( -2a + 3b) = (7xy - 2x)( -7xy - 2x) = Prof. Mapelli Rosangela 4a 2 - 49 9a 2 - 16b 2 4x 2 - 9y 2 a 4 - 9b 2 25a 2 - 9b 2 25a 4 - 4b 4 9a 6 - 4b 4 9b 2 - 4a 2 4x 2 - 49x 2 y 2

6. Quadrato di un binomio Prof. Mapelli Rosangela Il quadrato di un binomio è un trinomio avente per termini: il quadrato del 1° monomio il doppio prodotto del 1° monomio per il 2° il quadrato del 2° monomio

7. ESEMPI: Prof. Mapelli Rosangela (a + b) 2 = a 2 + 2( + a)( + b) + b 2 = a 2 + 2ab + b 2 (3a + 2b) 2 = 9a 2 + 2( + 3a)( + 2b) + 4b 2 = 9a 2 +12ab + 4b 2 (3a - b) 2 = 9a 2 + 2( + 3a)( - b) + ( - b) 2 = 9a 2 - 6ab + b 2 (- 4a + 2b) 2 =(4a) 2 + 2(- 4a)(+ 2b) + (2b) 2 = 16a 2 -16ab+ 4b 2 (3a 2 - 2ab) 2 =(3a 2 ) 2 + 2(3a 2 )(- 2ab) + (-2ab) 2 =9a 4 -2a 3 b+4a 2 b 2

8. Quadrato di binomio: esercizi (2a + 7) 2 = (3a - 4b) 2 = (-2x - 3y) 2 = (a 2 + 3b) 2 = (5a - 3b) 2 = (5a 2 + 2b 2 ) 2 = (-3a 3 + 2b 2 ) 2 = (2ab - 3b) 2 = (7xy - 2x) 2 = Prof. Mapelli Rosangela 4a 2 + 28 a + 49 9a 2 - 24 ab + 16b 2 4x 2 + 12 xy + 9y 2 a 4 + 6 a 2 b + 9b 2 25a 2 - 30ab + 9b 2 25a 4 + 20 a 2 b 2 + 4b 4 9a 6 - 12 a 3 b 2 + 4b 4 4a 2 b 2 - 12 ab 2 + 9b 2 49x 2 y 2 - 28 x 2 y + 4x 2

9. Cubo di un trinomio Prof. Mapelli Rosangela Il cubo di un binomio è un quadrinomio, cioè è formato da 4 monomi, avente per termini: il cubo del 1° monomio il triplo prodotto del quadrato del 1° per il 2° il triplo prodotto del 1° per il quadrato del 2° il cubo del 2° monomio

10. ESEMPI: Prof. Mapelli Rosangela (a + b) 3 = a 3 + 3(+ a) 2 (+ b) + 3(+ a)(+ b) 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3 (3a +2b) 3 = 27a 3 + 3(+ 3a) 2 (+ 2b)+ 3(+ 3a)(+ 2b) 2 + 8b 3 = 27a 3 + 54a 2 b + 36ab 2 +8b 3 (3a - b) 3 = 27a 3 + 3(+ 3a) 2 (- b) + 3(+ 3a)(- b) 2 + (- b) 3 = 27a 3 - 27 2 b + 9ab 2 - b 3 (- 4a + 2b) 3 = (- 4a) 3 + 3(- 4a) 2 ( + 2b) + 3(- 4a)(+ 2b) 2 + (2b) 3 = - 64a 3 + 96a 2 b - 48ab 2 + 8b 3 (3a 2 - 2ab) 2 = (3a 2 ) 3 + 3(3a 2 ) 2 (- 2ab) + 3(3a 2 )(- 2ab) 2 + (- 2ab) 3 = 27a 6 - 54a 5 b + 36a 4 b 2 - 8a 3 b 3

11. Cubo di binomio: esercizi (2a + 1) 3 = (3a - b) 3 = (-2x - 3y) 3 = (a 2 + 3b) 3 = (a - 3b) 3 = (a 2 + 2b 2 ) 3 = (-3a 3 + 2b 2 ) 3 = (2ab - 3b) 3 = Prof. Mapelli Rosangela 8a 3 +12a 2 +6a+1 27a 3 -27a 2 b+6ab 2 -b 3 -8x 3 -36x 2 y-54xy 2 -27y 3 a 6 +9a 4 b+27a 2 b 2 +27b 3 8a 3 -36a 2 b+54ab 2 -27b 3 a 6 +6a 4 b 2 +12a 2 b 4 +8b 6 -27a 9 +54a 6 b 2 -36a 3 b 4 +8b 6 8a 2 b 2 -36a 2 b 3 +54ab 3 -27b 3

12. Potenza di un binomio Prof. Mapelli Rosangela lo sviluppo di (a+b) n contiene sempre n+1 termini gli esponenti del primo termine decrescono mentre gli esponenti del secondo termine crescono i coefficienti possono essere disposti secondo uno schema detto il Triangolo di Tartaglia

13. ESEMPI: Prof. Mapelli Rosangela (2a + b) 4 = a 4 + 4(+ 2a) 3 (+ b) + 6(+ 2a) 2 (+ b) 2 + 4(+ 2a)(+ b) 3 + b 4 = a 4 + 32a 3 b + 24a 2 b 2 + 8ab 3 + b 4 (a - 2b) 5 = a 5 + 5(a) 4 (- 2b) + 10(a) 3 (- 2b) 2 + 10(a) 2 (- 2b) 3 + 5(a)(- 2b) 4 +(- 2b) 5 = a 5 - 10a 4 b + 40a 3 b 2 - 80a 2 b 3 + 80ab 4 - 32b 5 (3a - b) 4 = 81a 4 + 4( + 3a) 3 (- b) + 6(+ 3a) 2 (- b) 2 + 4( + 3a)(- b) 3 + (- b) 4 = 81a 4 - 108a 3 b + 54a 2 b 2 - 12ab 3 + b 4 (- a +2b) 5 = (- a) 5 + 5(- a) 4 (+ 2b)+ 10(- a) 3 (+ 2b) 2 +10(- a) 2 (+ 2b) 3 + 5(- a)(2b) 4 +(2b) 5 = - a 5 + 10a 4 b - 40a 3 b 2 + 80a 2 b 3 - 80ab 4 + 32b 5

14. Potenza n-esima di binomio: esercizi (2a - b) 4 = (a +b) 7 = (a - b) 7 = (a - b) 6 = (a +2b) 4 = (a - 2b) 4 = (a +2b) 5 = (-x - y) 5 = Prof. Mapelli Rosangela 16a 4 - 32a 3 b + 24a 2 b 2 - 8ab 3 + b 4 a 7 +7a 6 b+21a 5 b 2 +35a 4 b 3 +35a 3 b 4 +21a 2 b 5 +7ab 6 +b 7 a 4 + 8a 3 b + 24a 2 b 2 + 32ab 3 + 16b 4 a 4 - 8a 3 b + 24a 2 b 2 - 32ab 3 + 16b 4 a 6 - 6a 5 b +15a 4 b 2 - 20a 3 b 3 +15a 2 b 4 - 6ab 5 + b 6 a 7 -7a 6 b+21a 5 b 2 -35a 4 b 3 +35a 3 b 4 -21a 2 b 5 +7ab 6 -b 7 a 5 +10a 4 b + 40a 3 b 2 + 80a 2 b 3 +80ab 4 +32b 5 - x 5 - 5x 4 y - 10x 3 y 2 - 10x 2 y 3 - 5xy 4 - y 5

15. Triangolo di Tartaglia Prof. Mapelli Rosangela Triangolo di Tartaglia ogni riga inizia e termina con 1 ogni altro numero si ottiene sommando quelli sovrastanti della riga precedente

16. Chi era Tartaglia Prof. Mapelli Rosangela Niccolò Tartaglia, soprannome di Niccolò Fontana (Brescia, 1499 circa – Venezia, 13 dicembre 1557), è stato un matematico italiano, il cui nome è legato al noto triangolo Nacque da una famiglia poverissima. Durante la presa di Brescia da parte dei francesi nel 1512 il padre fu ucciso e lui stesso ferito alla mandibola e al palato. Dato per morto, sopravvisse grazie alle cure della madre, ma gli rimase una evidente difficoltà ad articolare le parole. Per questo ebbe il soprannome "Tartaglia" che accettò e lui stesso utilizzò tutta la vita per firmare le sue opere. Non poté frequentare alcuna scuola da giovane ed era molto fiero di essere autodidatta. Nei suoi scritti, si vanta infatti di essere andato a scuola di scrittura solo per 15 giorni, all'età di 14 anni. Grazie alla sua abilità, poté comunque guadagnarsi da vivere a Verona risolvendo l'equazione cubica o equazione di terzo grado. In realtà la formula era stata trovata, ma non pubblicata, da Scipione Dal Ferro nei primi del 1500, e fu nuovamente inventata dal Tartaglia una ventina di anni dopo, mentre sullo stesso problema lavoravano anche il professore Gerolamo Cardano e il suo discepolo Ludovico Ferrari più o meno nello stesso periodo. A Tartaglia dobbiamo tra l'altro la prima traduzione italiana degli Elementi di Euclide.

17. Quadrato del trinomio Prof. Mapelli Rosangela Il quadrato di un trinomio è un polinomio composto da 6 monomi, avente per termini: Il quadrato del primo termine, più il quadrato del secondo termine, più il quadrato del terzo termine il doppio prodotto del 1° per il 2° il doppio prodotto del 1° per il 3° il doppio prodotto del 2° per il 3°

18. ESEMPI: Prof. Mapelli Rosangela (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc (3a + 2b + c) 2 = 9a 2 + 4b 2 + c 2 + 2(+ 3a)(+ 2b)+ 2(+ 3a)(+ c)+ 2(+2b)(+ c)= 9a 2 + 4b 2 + c 2 + 12ab + 6ac + 4bc (3a - b + 2c) 2 = 9a 2 + (- b) 2 + (2c) 2 + 2(3a)(- b)+ 2(+ 3a)(2c) + 2(-b)(+2c) = 9a 2 + b 2 + 4c 2 - 6ab + 12ac - 4bc (c - 4a - 2b) 2 = c 2 + (- 4a) 2 + (- 2b) 2 + 2c(- 4a) + 2c(- 2b) + 2(- 4a)(- 2b) = c 2 + 16a 2 + 4b 2 - 8ac - 4bc + 16ab

19. Quadrato di polinomio: esercizi (2a + 2b + 7) 2 = (3a - 4b - 2c) 2 = (-2x - 3y + 1) 2 = (a 2 + 3b - c) 2 = (5a + 2b + c) 2 = (-3a 3 +2b 2 +1) 2 = (2ab - 3b - 2) 2 = (7xy - 2x - 1) 2 = Prof. Mapelli Rosangela 4a 2 +4b 2 +49+8ab+24a+24b 9a 2 +16b 2 +4c 2 -24ab-12ac+16bc 4x 2 +9y 2 +1+12 xy - 4x - 6y a 4 +9b 2 +c 2 + 6a 2 b - 2a 2 c - 6bc 25a 2 +4b 2 +c 2 +20ab+10ac+4bc 9a 6 +4b 4 +1 - 12a 3 b 2 - 6a 3 +4b 2 4a 2 b 2 +9b 2 +4-12ab 2 -8ab+12b 49x 2 y 2 +4x 2 +1- 28 x 2 y -14xy+4x

20. FINE Prof. Mapelli Rosangela A cura di Rosangela Mapelli www.nonsolomatematica.it