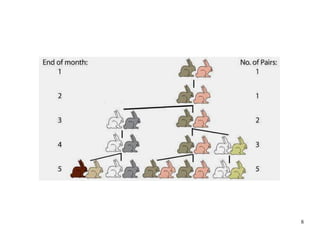
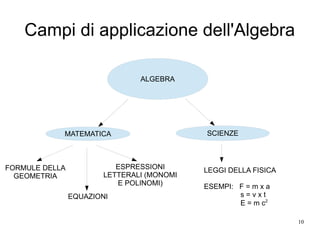
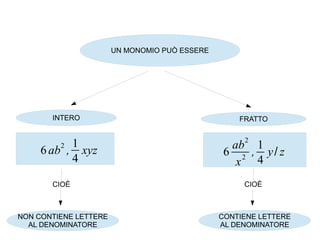
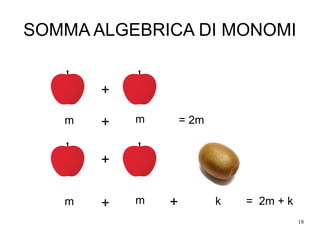
Il documento esplora i concetti fondamentali dell'algebra, inclusi monomi, polinomi e la loro applicazione nelle equazioni. Viene analizzata l'origine del termine 'algebra' e presentato un esempio pratico, insieme al celebre problema dei conigli di Fibonacci. Inoltre, si discutono le operazioni algebriche come somma, prodotto e divisione di monomi, e l'importanza delle funzioni nel descrivere relazioni matematiche.

1. Algebra
(espressioni letterali,
monomi e polinomi)

2. 2
Definizione
L'Algebra è una branca
della matematica
che tratta lo studio di
espressioni algebriche,
ovvero di espressioni
contenenti numeri
e lettere

3. 3
L'origine del termine
● Il termine algebra (dall'arabo ,‫بر‬ ‫ج‬ ‫ال‬ al-ğabr che significa "unione",
"connessione" o "completamento", ma anche "aggiustare") deriva dal
nome del libro del matematico persiano arabo Mu ammad ibn Mūsā al-ḥ
wārizmī, intitolato Al-Kitab al-Jabr wa-l- Muqabala ("Compendio sulḴ
Calcolo per Completamento e Bilanciamento"), che tratta la risoluzione
delle equazioni di primo e di secondo grado.

4. 4
Esempio
“Due volte una quantità incognita addizionata
a quattro unità sono eguali a 5 volte la stessa
quantità incognita”
L’espressione viene tradotta nel nostro
simbolismo con l’equazione: 2x + 4 = 5x.

5. 5

6. 6
I conigli di Fibonacci
C’è una coppia di conigli che si riproduce ogni
mese. Ogni nuova coppia si riproduce a sua
volta, ma a partire dal secondo mese di vita. La
prima coppia genera dopo ogni mese.
Quante coppie di conigli si avranno in un anno?

7. 7
Ecco come ragionò Fibonacci
I mese: A = la prima coppia di conigli ---> 1 coppia
II mese: A, B: la prima coppia ha generato ---> 2 coppie
III mese: A, B, C. C: coppia generata sempre dalla prima coppia ---> 3 coppie
IV mese: A, B, C, D, B1. D generata dalla coppia A, B1 dalla coppia B ---> 5
coppie
V mese: A, B, C, D, E, B1, B2, C1. 3 coppie in più: C1 dalla coppia C, E
dalla coppia A, B2 dalla coppia B ---> 8 coppie
VI mese: A, B, C, D, E, F, B1, B2, B3, B4, C1, C2, D1 5 coppie in più: F
dalla coppia A, B3 dalla coppia B, C2 dalla coppia C, B4 dalla coppia B1, D1
dalla coppia D ---> 13 coppie
E così via…..

8. 8

9. 9
Fn=Fn−1+Fn−2

10. 10
Campi di applicazione dell'Algebra
ALGEBRA
MATEMATICA SCIENZE
FORMULE DELLA
GEOMETRIA
EQUAZIONI
ESPRESSIONI
LETTERALI (MONOMI
E POLINOMI)
LEGGI DELLA FISICA
ESEMPI: F = m x a
s = v x t
E = m c2

11. 11
Ma a che serve l'algebra?

12. 12
I Monomi

13. 13

14. 14

15. 15

16. 16
UN MONOMIO PUÒ ESSERE
INTERO FRATTO
CIOÈ
NON CONTIENE LETTERE
AL DENOMINATORE
CIOÈ
CONTIENE LETTERE
AL DENOMINATORE
6 ab
2
,
1
4
xyz 6
ab2
x
2
,
1
4
y/ z

17. 17

18. 18
SOMMA ALGEBRICA DI MONOMI
+
m m+ = 2m
+
+m + m k = 2m + k

19. 19
QUINDI …
DUE O PIÙ MONOMI SI POSSONO SOMMARE
SOLO SE SONO SIMILI

20. 20

21. 21
PRODOTTO DI MONOMI
6ab
2
⋅(−2)a b
3
=−12a
2
b
4
SI MOLTIPLICANO TRA LORO I COEFFICIENTI E LA PARTE LETTERALE

22. 22

23. 23

24. 24
DIVISIONE DI MONOMI
6a
2
b
2
:(−2)ab
3
=−3(a
2
:a)⋅(b
2
:b
3
)=−3ab
−1

25. 25

26. 26

27. 27
POTENZA DI UN MONOMIO
A=x2
x

28. 28
POTENZA DI UN MONOMIO
A=x2
x
2x
A=(2 x)2
=22
x2
=4 x2

29. 29

30. 30
I Polinomi

31. 31

32. 32
Esercizi
● Nei seguenti monomi indica il coefficiente e la
parte letterale
● Riduci i seguenti monomi in forma normale
+9ab
2
−5ab2
c4
+
3
4
a
2
b
3
c
2
−
1
7
a
2
b
4
−5ab
2
c
4
−5ab
2
c
4
−9a
3
bab⋅(−2) 1
3
xy⋅(−4)⋅x2

33. 33
● Scrivi tre monomi simili al monomio 4ab aventi
come coefficienti rispettivamente i numeri
● Esegui le seguenti somme algebriche di
monomi
−
2
5
, +
3
8
, −1, −
1
7
3x+(−7x)+(+12x)
3ab+(−2a)−(−ab)+(−5a)

34. 34
● Esegui le seguenti moltiplicazioni e divisioni di
monomi
(−56b
4
c):(−8b
3
c)
−8x
3
y
4
⋅(+2xy
2
)
3
2
ab⋅(9
4
a
2
b
2
)
(−
14
9
x
6
y
4
):(−
7
3
x
5
z)

35. 35

36. 36

37. 37
I MONOMI COME FUNZIONI

38. 38
Immaginiamo di avere una pianta
che cresce di un metro all'anno
All'età di un anno misurerà un metro
A 2 anni, 2 metri
A 3 anni, 3 metri
A x anni, x metri

39. 39
● Chiamiamo y l'altezza della pianta e x il tempo
● Allora possiamo scrivere
y = x
QUINDI L'ALTEZZA DELL'ALBERO È UN MONOMIO

40. 40
Cos'è una funzione
● Una funzione è una relazione matematica che
ad ogni valore della variabile indipendente (x)
fa corrispondere un valore della variabile
dipendente (y)
● Matematicamente si indica: y =f(x) e si
legge :” y è funzione di x”
● Nel nostro caso:
y = x se x = 1 → y = 1
se x = 2 → y = 2
se x = k → y = k

41. 41
Applicazioni nella geometria e nella fisica

42. 42
Area del quadrato
● Se chiamiamo y l'area e x il lato troviamo che
l'area è un monomio ed è funzione del lato
x
¿
y=x2 x = 1 → y = 12
= 1
x = 2 → y = 22
= 4

43. 43
Moto rettilineo uniforme (s =v·t)
● Se chiamiamo y lo spazio percorso è x il
tempo troviamo che lo spazio è un monomio
ed è funzione del tempo
¿
y=k⋅x¿
velocitàspazio tempo