Downloaded 79 times
Uploaded byGerardina Cientanni
Prismi e-piramidi
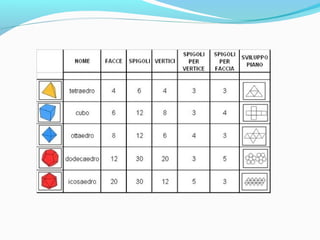
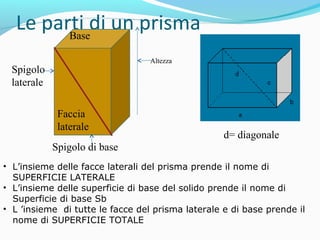
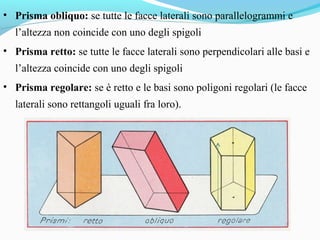
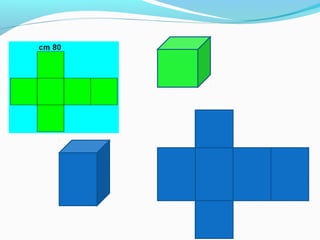
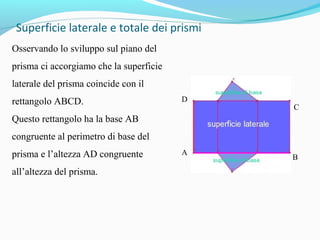
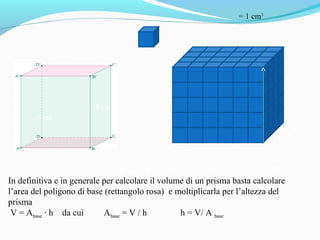
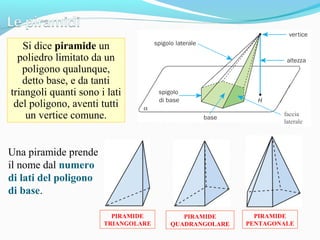
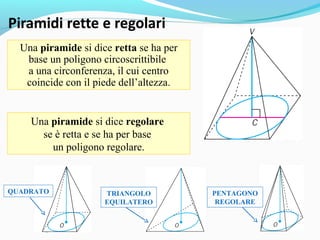
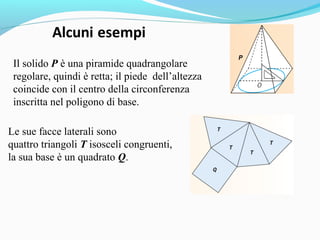
Il documento analizza i poliedri e i solidi, definendo poliedri regolari, prismi e piramidi, con spiegazioni dettagliate su superficie, volume e relazioni geometriche. Si evidenziano le formule per calcolare superficie e volume di prismi e piramidi, sottolineando l'importanza delle unità di misura. L'argomento viene accompagnato da esempi pratici e distintivi nell'uso di termini come superficie e area.
![Le tre leggi di keplero [prof. santi caltabiano]](https://cdn.slidesharecdn.com/ss_thumbnails/letreleggidikepleroprof-190913155739-thumbnail.jpg?width=640&height=640&fit=bounds)
Prismi e-piramidi
- 1.
- 2. Abbiamo visto chei solidi si suddividono in… Poliedri, se la sua superficie è formata esclusivamente da poligoni Solidi a superficie curva se, la sua superficie è parzialmente curva
- 3. Poliedri regolari Un poliedroè regolare se tutte le sue facce sono poligoni regolari e congruenti e tutti i diedri e gli angoloidi sono congruenti fra loro I Poliedri regolari sono solo cinque e prendono il nome di solidi platonici
- 6. Un prisma è Unpoliedro costituito da due poligoni congruenti, posti su piani paralleli, e da tanti parallelogrammi quanti sono i lati di ciascuno dei due poligoni di base I poligoni di base danno il nome al prisma
- 7.
- 8. Le parti diun prisma Base Altezza Spigolo laterale Faccia laterale d= diagonale Spigolo di base • L’insieme delle facce laterali del prisma prende il nome di SUPERFICIE LATERALE • L’insieme delle superficie di base del solido prende il nome di Superficie di base Sb • L ’insieme di tutte le facce del prisma laterale e di base prende il nome di SUPERFICIE TOTALE
- 9. • Prisma obliquo:se tutte le facce laterali sono parallelogrammi e l’altezza non coincide con uno degli spigoli • Prisma retto: se tutte le facce laterali sono perpendicolari alle basi e l’altezza coincide con uno degli spigoli • Prisma regolare: se è retto e le basi sono poligoni regolari (le facce laterali sono rettangoli uguali fra loro).
- 10. La superficie diun solido Per visualizzare la superficie di un solido si ricorre ad una operazione chiamata “sviluppo sul piano del solido” e ci permette di capire come si calcola la misura dell’area di un solido. Lo sviluppo di un solido è la superficie che si ottiene riportando su un piano le facce che lo compongono. Lo sviluppo di un solido consiste nel distendere su una superficie piana tutte le facce, laterali e di base, del solido.
- 12. Superficie laterale etotale dei prismi Osservando lo sviluppo sul piano del prisma ci accorgiamo che la superficie laterale del prisma coincide con il rettangolo ABCD. D C Questo rettangolo ha la base AB congruente al perimetro di base del prisma e l’altezza AD congruente all’altezza del prisma. A B
- 13. In definitiva lasuperficie laterale del prisma si ottiene moltiplicando il perimetro del poligono di base del prisma per l’altezza: Sl = p x h P= Sl : h h = Sl : p P.s. ricorda dire superficie o dire Area è la stessa cosa
- 14. Superficie totale La superficietotale è data dalla somma della superficie laterale e dell’area delle due basi: St = Sl + 2Ab Formule inverse Sl = St – 2Ab Ab = (St – Sl )/2
- 15. Il volume deiprismi Per comprendere la formula che ci permette di calcolare il volume di un prisma, consideriamo il caso di un parallelepipedo rettangolo avente le dimensioni di base di 4 cm e 6 cm e l’altezza di 5 cm. Scegliamo come unità di misura il cm3, calcolare il volume del parallelepipedo significa trovare quanti cubetti con lo spigolo da 1 cm3, esso può contenere.
- 16. = 1 cm3 5cm 4 cm 6 cm 6 cm x 4 cm = 24 cm x 5 cm = 120cm3 In definitiva e in generale per calcolare il volume di un prisma basta calcolare l’area del poligono di base (rettangolo rosa) e moltiplicarla per l’altezza del prisma V = Abase ∙ h da cui Abase = V / h h = V/ A base
- 17. Avvertimento !!!!! Quando devitrovare il Volume dei solidi ricordati che devi stare attento all’unità di misura Se V è in Allora P è in E Ps è in dm3 Kg Kg/dm3 cm3 g g/cm3 m3 t t/m3
- 18. Il rapporto trapeso e volume di una sostanza prende il nome di peso specifico (ps) Ps = P/V P = Ps x V V = P / Ps Quindi il volume di un corpo si può ricavare dal peso specifico della sostanza
- 19. il parallelepipedo rettangolo Sei poligoni di base sono dei rettangoli abbiamo il c parallelepipedo rettangolo, tutte e 6 le facce sono quindi dei rettangoli a due a due congruenti e paralleli. I tre spigoli che escono b a da uno stesso vertice si chiamano V=a∙b∙c dimensioni del parallelepipedo e a = V / b∙c sono lunghezza larghezza e altezza b = V / a∙c c = V / a ∙b
- 20. Il cubo èun particolare parallelepipedo rettangolo avente le tre dimensioni congruenti Nel caso del cubo, poiché le facce sono quadrati congruenti sarà sufficiente trovare l’area di una faccia e moltiplicarla per 4 per avere l’area della superficie laterale e per 6 per avere l’area della superficie totale Slaterale = Abase ∙ 4 = l2 ∙ 4 l= Stotale = Abase ∙ 6 = l2 ∙ 6 l=
- 21.
- 22. Si dice piramideun poliedro limitato da un poligono qualunque, detto base, e da tanti triangoli quanti sono i lati del poligono, aventi tutti un vertice comune. faccia laterale Una piramide prende il nome dal numero di lati del poligono di base. PIRAMIDE TRIANGOLARE PIRAMIDE QUADRANGOLARE PIRAMIDE PENTAGONALE
- 23. Una piramide sidice retta se ha per base un poligono circoscrittibile a una circonferenza, il cui centro coincide con il piede dell’altezza. Una piramide si dice regolare se è retta e se ha per base un poligono regolare. QUADRATO TRIANGOLO EQUILATERO PENTAGONO REGOLARE
- 24. Il solido Pè una piramide quadrangolare regolare, quindi è retta; il piede dell’altezza coincide con il centro della circonferenza inscritta nel poligono di base. Le sue facce laterali sono quattro triangoli T isosceli congruenti, la sua base è un quadrato Q.
- 25. In una piramideretta le facce triangolari laterali hanno tutti la stessa altezza, che prende il nome di apotema ATTENZIONE!!!! Non confondere l’apotema della piramide con l’apotema del poligono di base che coincide con il raggio della circonferenza
- 26. Come avrai notatol’apotema di una piramide coincide con l’ipotenusa di un triangolo rettangolo che ha come cateti l’altezza della piramide e il raggio della circonferenza inscritta nel altezza apotema poligono. raggio LO HAI NOTATO?!!!!? POSSIAMO ALLORA RICORRERE AL TEOREMA DI PITAGORA PER TROVARE I TRE SEGMENTI?
- 27. Osservando lo svilupposul piano di una piramide regolare si nota che la superficie laterale è formato da tanti triangoli quanti sono i lati del poligono di base. Questi triangoli, hanno tutti la stessa altezza (apotema della piramide). Questi triangoli sono equivalenti a un unico triangolo che ha per base il perimetro del poligono di base e per altezza l’apotema della piramide.
- 28. Poiché l’area deltriangolo è A = (b ∙ h) : 2 la superficie laterale è Sl = (2p ∙ a) : 2 da cui 2p = (2 ∙ Sl) : a a = (2 ∙ Sl ) : 2p La superficie totale si trova come nei prismi
- 29. Il volume della piramide Percapire come si calcola il volume della piramide possiamo ricorrere ad un esperimento. Costruiamo una piramide e un prisma con lo stesso poligono di base e la stessa altezza. Riempiamo la piramide di sabbia e versiamola nel prisma. Che cosa noti? Poiché il volume del prisma si ottiene V = Abase ∙ h Il volume della piramide è V = (Abase ∙ h) : 3