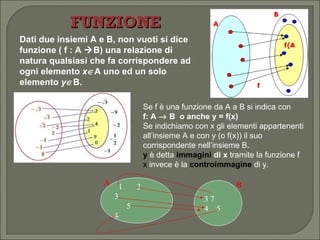
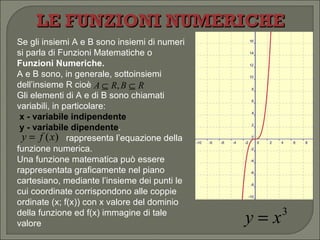
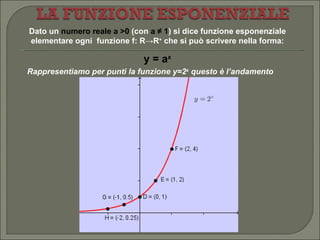
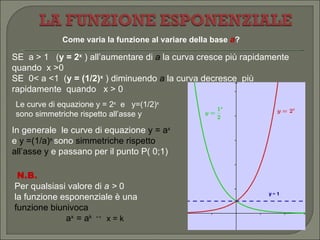
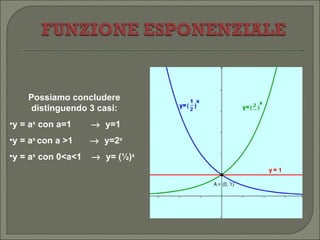
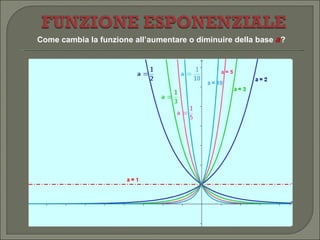
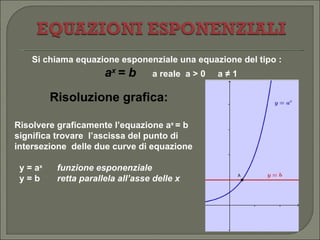
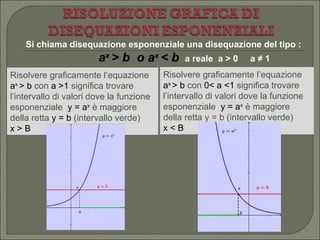
Il documento esplora la funzione esponenziale, trattando obiettivi di apprendimento come il riconoscimento, la grafica e la risoluzione di equazioni e disequazioni esponenziali. Espone le proprietà delle funzioni numeriche, i concetti di dominio e codominio, e fornisce dettagli su come risolvere equazioni esponenziali sia graficamente che algebricamente. Infine, descrive diverse situazioni riguardanti l'andamento della funzione al variare della base e le regole di comportamento relative a esse.

1. Creato da: Rosangela Mapelli www.nonsolomatematica.it Licenza Cretive Commons: Sei libero di modificare e pubblicare questa Presentazione a patto di indicare l'autore, non trarne guadagno e devi condividere i derivati sotto la stessa licenza. LA FUNZIONE ESPONENZIALE

2. OBIETTIVI PREREQUISITI Riconoscere e disegnare la funzione esponenziale Saper risolvere equazioni esponenziali Saper risolvere equazioni esponenziali graficamente Saper risolvere disequazioni esponenziali Proprietà delle potenze Equazioni di I e II grado Funzioni e loro proprietà Dominio e codominio di una funzione Alcuni di questi argomenti verranno riproposti nelle prime slide

3. Dati due insiemi A e B, non vuoti si dice funzione ( f : A  B) una relazione di natura qualsiasi che fa corrispondere ad ogni elemento x  A uno ed un solo elemento y  B. FUNZIONE Se f è una funzione da A a B si indica con f: A  B o anche y = f(x) Se indichiamo con x gli elementi appartenenti all’insieme A e con y (o f(x)) il suo corrispondente nell’insieme B. y è detta immagini di x tramite la funzione f x invece è la controimmagine di y. 1 2 3 5 4 3 7 4 5 A B

4. LE FUNZIONI NUMERICHE Se gli insiemi A e B sono insiemi di numeri si parla di Funzioni Matematiche o Funzioni Numeriche. A e B sono, in generale, sottoinsiemi dell’insieme R cioè Gli elementi di A e di B sono chiamati variabili, in particolare: x - variabile indipendente y - variabile dipendente . rappresenta l’equazione della funzione numerica. Una funzione matematica può essere rappresentata graficamente nel piano cartesiano, mediante l’insieme dei punti le cui coordinate corrispondono alle coppie ordinate (x; f(x)) con x valore del dominio della funzione ed f(x) immagine di tale valore

5. DOMINIO E CODOMINIO Si definisce dominio D (o Campo di Esistenza CdE, o anche insieme di definizione) della funzione reale di variabile reale è il più ampio sottoinsieme di R costituito da tutti e soli i valori della x ( variabile indipendente ) per cui esistano finiti i corrispondenti valori di y = f(x), cioè ammetta almeno un’immagine in y Si definisce codominio C di una funzione il sottoinsieme di R costituito da tutti gli elementi y ( variabile dipendente ). corrispondenti dei punti x appartenenti al dominio della funzione cioèl’insieme delle immagini della variabile x.

6. Casi particolari:

7. Dato un numero reale a >0 (con a ≠ 1 ) si dice funzione esponenziale elementare ogni funzione f: R->R + che si può scrivere nella forma: y = a x Rappresentiamo per punti la funzione y=2 x questo è l’andamento

8. Come varia la funzione al variare della base a ? SE a > 1 ( y = 2 x ) all’aumentare di a la curva cresce più rapidamente quando x >0 SE 0< a <1 ( y = (1/2) x ) diminuendo a la curva decresce più rapidamente quando x > 0 Le curve di equazione y = 2 x e y=(1/2) x sono simmetriche rispetto all’asse y In generale le curve di equazione y = a x e y =(1/a) x sono simmetriche rispetto all’asse y e passano per il punto P( 0;1) N.B. Per qualsiasi valore di a > 0 la funzione esponenziale è una funzione biunivoca a x = a k ↔ x = k

9. - Il dominio della funzione è  D =  = (-  ;+  ) - Il codominio della funzione è  + C =  + = (0; +  ) - E’ sempre positiva - Interseca l’asse delle ordinate nel punto (0;1) Se a>1 La funzione è sempre crescente Se x  +  la funzione tende a +  Se x  -  la funzione tende a 0 quindi l’asse delle ascisse è asintoto orizzontale Se 0<a<1 La funzione è sempre decrescente Se x  +  la funzione tende a 0 quindi l’asse delle ascisse è asintoto orizzontale Se x  -  la funzione tende a +  y = a x con a > 0 e a ≠ 1

10. Possiamo concludere distinguendo 3 casi: y = a x con a=1  y=1 y = a x con a >1  y=2 x y = a x con 0<a<1  y= (½) x

11. Come cambia la funzione all’aumentare o diminuire della base a ?

12. Si chiama equazione esponenziale una equazione del tipo : a x = b a reale a > 0 a ≠ 1 Risoluzione grafica: Risolvere graficamente l’equazione a x = b significa trovare l’ascissa del punto di intersezione delle due curve di equazione y = a x funzione esponenziale y = b retta parallela all’asse delle x

13. Risoluzione algebrica Per determinare la soluzione dell’equazione a x = b si deve quindi riscrivere l’equazione in modo che entrambi i membri siano potenze della stessa base a Es: 2 x = 8 -> 2 x = 2 3 Ricordiamo che la funzione esponenziale y = a x è una funzione biunivoca e quindi: a x = a k ↔ x = k due potenze con la stessa base sono uguali solo se sono uguali i loro esponenti Si dice che l’equazione esponenziale a x = a k è ridotta in forma canonica Possiamo quindi uguagliare gli esponenti dell’equazione ottenendo x = 3 che è la soluzione dell’equazione iniziale Attenzione !! Non sempre una equazione esponenziale può essere ridotta in forma canonica; In questi casi dobbiamo ricorrere ai logaritmi

14. In generale possiamo dire che l’equazione esponenziale: a x = b con a > 0 e a ≠ 1 è determinata e ammette una sola soluzione se b > 0 impossibile se b ≤ 0 Risolvendo un’equazione ridotta alla forma a x = b, possono presentarsi due casi: b è una potenza di a : è sufficiente in questo caso risolvere l’equazione ottenuta uguagliando gli esponenti b non è una potenza di a: si risolve l’equazione ottenuta considerando i logaritmi dei suoi due membri

15. ESEMPI Poniamo t = 3 x Risolviamo l’equazione di secondo grado e troviamo da cui e 1. 2. 3. 4.

16. Si chiama disequazione esponenziale una disequazione del tipo : a x > b o a x < b a reale a > 0 a ≠ 1 Risolvere graficamente l’equazione a x > b con a >1 significa trovare l’intervallo di valori dove la funzione esponenziale y = a x è maggiore della retta y = b (intervallo verde) x > B Risolvere graficamente l’equazione a x > b con 0< a <1 significa trovare l’intervallo di valori dove la funzione esponenziale y = a x è maggiore della retta y = b (intervallo verde) x < B

17. Risoluzione algebrica Per determinare la soluzione della disequazione a x > b si deve quindi riscrivere l’equazione in modo che entrambi i membri siano potenze della stessa base a , bisogna poi distinguere i due casi : La base a >1 Es: La base 0 < a < 1 Es: a x > a k o a x > a k si dice che la disequazione esponenziale è ridotta in forma canonica Attenzione al segno