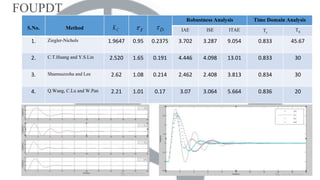
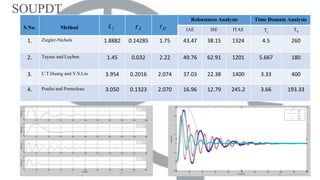
This document compares different PID controller tuning methods for first-order and second-order unstable processes with dead time (FOUPDT and SOUPDT). It analyzes the Ziegler-Nichols, C.T. Huang and Y.S. Lin, Shamsuzzoha and Lee, and Q. Wang et al. tuning methods for FOUPDT processes, finding that the Shamsuzzoha and Lee method provides the best response with minimum IAE, ISE, and ITAE. For SOUPDT processes, it analyzes the Ziegler-Nichols, Tayrus and Luyben, C.T. Huang and Y.S. Lin, and P

1. COMPARISON OF PID CONTROLLER TUNING METHODS FOR FOPDT AND
SOPDT OF UNSTABLE SYSTEM
Paper ID:1037
Presented by,
Nidhi Yadav, M.Tech Scholar
Supervised By,
Mr. S.K.Sharma
(Assistant Professor)
Chemical Engineering Department
Deenbandhu Chhotu Ram University of Science and Technology, Murthal(Haryana), India

2. CONTENT
• PID Controller
• Unstable System
• Controller Tuning
• Process and Tuning Methods
• FOUPDT (First order unstable process with dead time)
• SOUPDT (Second order unstable process with dead time)
• Conclusion
• References

3. PID CONTROLLER
• It is most commonly used in control process for better stability of the process
• It combines the beneficial features of PD and PI controller
• It gives lower overshoot
• It eliminate derivative and proportional Kick
• It gives direct and reverse action
• It consist automatic and manual control modes
• It has lower rise and settling time
• In chemical industry desired output (product) of the process needed in small time with out taking any
deficiency
G(s) is transfer function of PID controller and , , are controller parameter
1
( ) [1 ]C D
I
G s K s
s


  
CK I D

4. UNSTABLE SYSTEM
• An initially system is said to be unstable if bounded input produces unbounded output
• Unstable system shows erratic and extreme behavior
• It can not restore themselves to equilibrium
• It exceed performance level of stable system but lose stability
• Roots of unstable system lies in right hand of s-plane
G(s) is transfer function of Unstable system, Where , are process gain and time constant respectively
• Batch Reactor system is an unstable system which considered here
• When an exothermic reaction take place in Batch Reactor then it become an Unstable system
( )
( 1)
PK
G s
s


PK 

5. CONTROLLER TUNING
• Controller tuning refers to the selection of tuning parameters to ensure the best response of the controller
• The experimentation for optimum values of the controller parameter with respect to a particular process is
Controller tuning
Dead Time:
Output variable does not response immediately to a change in the input variable this condition called dead
time.
Standard transfer function of first and second order unstable process with dead time given below,
FOUPDT SOUPDT
( )
( 1)
s
PK e
G s
s




 1 2
( )
( 1)( 1)
s
PK e
G s
s s

 


 
( ) s
dG s e 


6. PROCESS AND TUNING METHODS
• FOUPDT
• Tuning Methods
1. Ziegler-Nichols
2. C.T.Huang and Y.S.Lin
3. Shamsuzzoha and Lee
4. Q.Wang, C.Lu and W.Pan
• SOUPDT
• Tuning Methods
1. Ziegler-Nichols
2. Tayrus and Luyben
3. C.T.Huang and Y.S. Lin
4. Poulin and Pomerleau
0.4
1.
( )
1. 1
s
e
G s
s



0.939
1.
( )
(5. 1)(2.07 1)
s
e
G s
s s


 

7. FOUPDT
S.No. Method
Robustness Analysis Time Domain Analysis
IAE ISE ITAE Tr TS
1. Ziegler-Nichols 1.9647 0.95 0.2375 3.702 3.287 9.054 0.833 45.67
2. C.T.Huang and Y.S.Lin 2.520 1.65 0.191 4.446 4.098 13.01 0.833 30
3. Shamsuzzoha and Lee 2.62 1.08 0.214 2.462 2.408 3.813 0.834 30
4. Q.Wang, C.Lu and W.Pan 2.21 1.01 0.17 3.07 3.064 5.664 0.836 20
CK I D

8. SOUPDT
S.No. Method
Robustness Analysis Time Domain Analysis
IAE ISE ITAE Tr TS
1. Ziegler-Nichols 1.8882 0.14285 1.75 43.47 38.15 1324 4.5 260
2. Tayrus and Luyben 1.45 0.032 2.22 49.76 62.91 1201 5.667 180
3. C.T.Huang and Y.S.Lin 3.954 0.2016 2.074 37.03 22.38 1400 3.33 400
4. Poulin and Pomerleau 3.050 0.1323 2.070 16.96 12.79 245.2 3.66 193.33
CK I D

9. CONCLUSION
• PID controller designed for FOUPDT and SOUPDT by different controller tuning
methods.
• All methods are worked in direction of settling the process variable to a desired set value.
• For FOUPDT; IAE, ISE and ITAE are very minimum by Shamsuzzoha and Lee method as
compared to other controller tuning methods, this shows that this method gives very good
response and robust performance of controller for first order unstable process without
taking too much time and oscillation for attain stability of the system.
• For SOUPDT; IAE, ISE and ITAE are very minimum by Poulin and Pomerleau method as
compared to other controller tuning method, this shows this method gives very good and
robust performance of controller for second order unstable process without taking too
much time and oscillation for attain stability of the system.

10. REFERENCES
• Shamsuzzoha, M.; Lee, M. IMC-PID controller design for improved disturbance rejection of time
delayed processes; Ind. Eng. Chen. Res.2007; 46, 2077-2091.
• Huang, C. T., & Lin, Y. S. Tuning PID controller for open-loop unstable processes with time delay.
Chemical Engineering Communications, 1995; 133, 11.
• Poulin, ED., & Pomerleau, A. PID tuning for integrating and unstable processes. IEE Process Control
Theory and Application, 1996; 143(5), 429.
• Qing Wang, Changhou Lu, Wei Pan, IMC PID controller tuning for stable and unstable processes
with time delay, Chemical Engineering Research and Design, 2015; 42.
• Tyreus, B. D.; Luyben, W. L. Tuning PI controllers for integrator/dead time processes. Ind. Eng.
Chem. Res. 1992, 2625−2628.
• Seborg, Edgar, Mellichap, Doyle Process Dynamics and control; 2011; Edition 3rd page no. 223-225.
• Donald R. Coughanour, Process System Analysis and Control;1991; Edition 2nd page no. 54
• Shahian, B., & Hassul, M. Control system design using MATLAB. Englewood Cli!s, 1993; NJ:
Prentice Hall.

11. THANK YOU