This document discusses the design, implementation, and applications of controllers. It describes how controllers can be designed in the time domain or frequency domain. The main types of controllers discussed are proportional (P), proportional-derivative (PD), proportional-integral (PI), and proportional-integral-derivative (PID) controllers. It explains how each type of controller affects the transient response and steady-state response by improving damping ratio, reducing settling time and overshoot, and reducing steady-state error. The effects of adding poles and zeros to open-loop and closed-loop transfer functions are also covered. Finally, an example application of using a PID controller for speed and torque control of a wind generator connected to the power grid is mentioned.

1. Design, Implementation, and
Applications of Controllers
Design, Implementation, and
Applications of Controllers
Dr. S. P. Gawande
MIEEE, LMISTE. MIACSIT, MIE(I)
spgawande_18@yahoo.com

2. Control System
Control System
14-Mar-20 2

3. Design of Controller
Design of Controller
•The design of the controller can be carried out either in time
domain or frequency domain
• In Time domain the specifications used are Maximum (Peak)
Overshoot, Rise Time and Settling time.
Overshoot, Rise Time and Settling time.
• In frequency domain the specifications used are Gain Margin,
Phase Margin, Resonant Peak.
• The choice of the controller design depends on the preference
of the designer and the complexity of the system.

4. Types of Controllers
Types of Controllers
Controllers in Time Domain
• Proportional Controller
• Proportional Derivative Controller (PD Controller)
• Proportional Integral Controller (PI Controller)
• Proportional Integral Derivative Controller (PID Controller)
• Proportional Integral Derivative Controller (PID Controller)
Controllers in Frequency Domain
• Lead Compensator
• Lag compensator
• Lag-Lead Compensator
• Notch Controller
14-Mar-20 4

5. Role of Controllers to Improve Transient Response and
Steady state Response
Role of Controllers to Improve Transient Response and
Steady state Response
Transient Response
• Increase in Damping ration ( )
• Reduction in Peak overshoot (MP %)
• Reduction in settling time (Ts)
Steady state Response
ξ
Steady state Response
• Reduction in Steady State Error (Ess)
• Increase in Gain (k)
• Increase in Type of the System
14-Mar-20 5

6. Proportional Controller and Addition of Poles and Zeros
Proportional Controller and Addition of Poles and Zeros
• The controller has been typically a simple amplifier with a constant gain
Kp. This type of control action is formally known as proportional control,
because the control signal at the output of the controller is simply related to
the input of the controller by a proportional constant (Kp)
• Along with the derivative and integral controller, these controllers add
additional poles and zeros to the open loop or the close loop transfer function
of the overall system.
• Addition or cancellation of undesirable poles and zeros of TF often
necessary in achieving the satisfactory time domain performance of control
system.

7. Uncompensated System (or With Only Proportional
controller)
Uncompensated System (or With Only Proportional
controller)
• Proportional Controller : The controller in which the
controller output is proportional to the error signal
• The uncompensated 2nd order system for under damped system
is given by
is given by
2
, ( )
( 2 )
n
Where G S
S S n
ω
ξω
=
+
14-Mar-20 7

8. With Proportional Controller
2
( )
K p n
G S
ω
=
Effects :
1. Increases the Gain of the System
2. Generate impact similar to the shifting of the pole away from
the origin
( )
( 2 )
K p n
G S
S S n
ω
ξω
=
+
14-Mar-20 8

9. Derivative Error compensation (Derivative Error Controller)
Error Rate Controller
Derivative Error compensation (Derivative Error Controller)
Error Rate Controller
Objective :
1) To improve Transient Response by improving Damping ( )
3) To reduce the Peak overshoot (%Mp) and Settling time (Ts)
Derivative Controller/PD Controller : The input to the plant is
the combination/sum of two signals. One is proportional to
ξ
the combination/sum of two signals. One is proportional to
the error signal while the other is proportional to the
derivative of error signal
Where , Kp = Proportional Gain , KD = Derivative Error
Constant / Derivative Gain of the controller
( ( ))
( ) ( )
d e t
Vc t K e t K
p D
dt
= +
( ) ( ) ( )
Vc S K E S K S E S
p D
= +
14-Mar-20 9

10. 2(1 )
( )
2
( ) ( 2 ) (1 )
n SK
C S D
R S S S n n SKD
ω
ξω ω
+
=
+ + +
1
2
K n
D ω
ξ ξ
= +
14-Mar-20 10

11. Derivative Output compensation (Derivative Output
Controller) Output Rate Controller
Derivative Output compensation (Derivative Output
Controller) Output Rate Controller
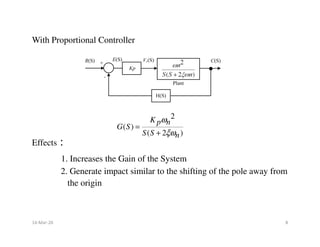
Objective :
1) To improve the Transient Response by improving ( )
3) To reduce the Peak overshoot (%Mp) and Settling time (Ts)
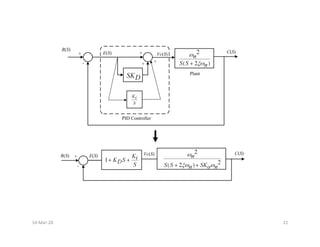
Derivative Controller/PD Controller : The derivative of the
output signal is compared with the error signal and the
ξ
output signal is compared with the error signal and the
resultant is given as input to the plant.
[ ( )]
( ) ( )
( ) ( ) ( )
d C t
V t e t K
c o
dt
V S E S K S C S
c o
= −
= −
Where , Ko = Derivative output Constant / Tachometer
feedback constant
14-Mar-20 11

12. 2
( )
2 2 2
( ) (2 )
C S n
R S S K S n
n o n
ω
ξω ω ω
=
+ + +
1
2
K o n
ω
ξ ξ
= +
14-Mar-20 12

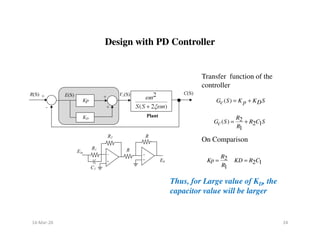
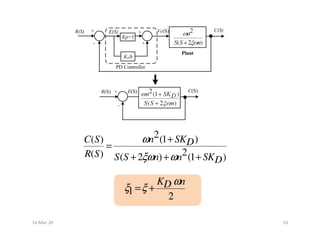
13. Effect of Addition of Zero to the Close loop Transfer Function
(Unity Feedback System)
Effect of Addition of Zero to the Close loop Transfer Function
(Unity Feedback System)
Consider a closed loop T.F. of second order uncompensated system
Consider a zero S = -1/KD to be added to the prototype of second
order T.F.
2
2
( )
2 2
( ) 2
Y S n
R S S nS n
ω
ξω ω
=
+ +
2(1 )
( )
2 2
( ) 2
2
2
( )
2 2 2 2
( ) 2 2
[ ( )]
( ) 1
( )
1
( )
n K S
Y S D
R S S nS n
K S n
Y S n D
R S S nS n S nS n
d Y t
Y S
Y t KD
R S dt
ω
ξω ω
ω
ω
ξω ω ξω ω
+
=
+ +
= +
+ + + +
= +
For ωn = 1, ξ = 0.5 and KD = 0, 1, 3, 6, 10
14-Mar-20 13

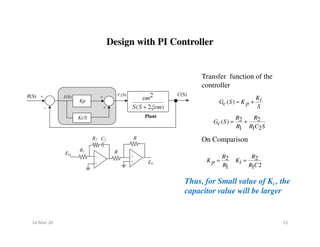
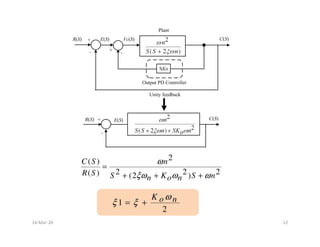
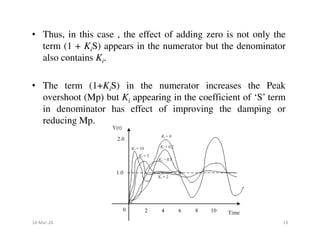
14. • As KD increases, zero will move closer to the origin, thus decreasing the
rise time and increasing the peak overshoot (Mp)
• Thus Y1(t) increases by after adding a zero to the close loop T.F..
Thus it increases the Mp and decreases the rise time.
• As KD approaches to infinity, Mp also approaches to infinity and yet the
system is stable as long as peak overshoot (Mp) is finite and damping is
positive.
[ 1( )]
d Y t
KD
dt
14-Mar-20 14

15. Effects of PD Controller
Effects of PD Controller
• The Damping ratio/Factor is increased from by factor
as compared with damping factor of uncompensated system. (The
damping ratio can be increased to any desired value with suitable choice of
Ko or KD)
• The increase in damping reduces the Peak overshoot as
2 2
k K
D n o n
ω ω
=
πξ
−
1
ξ ξ
−
• The Increase in damping reduces the Settling Time as
• At optimal value of Kp and Kd, controller reduces the settling time
and also rise time.
• Improves Bandwidth and improves GM, PM and Mr. (In frequency
Domain)
2
1
%Mp e
πξ
ξ
−
−
=
4 3
Ts
n n
ξω ξω
= =
14-Mar-20 15

16. Integral Controller/Compensation/Integral Error
Compensation (PI Controller)
Integral Controller/Compensation/Integral Error
Compensation (PI Controller)
Objective :
1) To improve the Steady State Response of the system
2) To increase the Type of the system
Integral or PI Controller : The input to the Plant is the
combination of sum of two signals. One is proportional to the
combination of sum of two signals. One is proportional to the
error signal and other is proportional to integral of error
signal.
( ) ( ) ( ).
0
( ) ( ) ( )
V t e t K e t dt
c i
Ki
V S E S E S
c
S
∞
= + ∫
= +
Where , Ki = Integral Error Constant/ Gain of the Integral
controller
14-Mar-20 16

17. Thus the Loop Transfer function of the compensated system
with integral controller is
2( )
( ) ( )
2( 2 )
n S Ki
G S H S
S S n
ω
ξω
+
=
+
Thus with integral controller, the Type of the system increases
to 2 from 1.
14-Mar-20 17

18. Effect of Addition of zero to the Forward Path Transfer
Function
Effect of Addition of zero to the Forward Path Transfer
Function
Consider a second order unity feedback system with forward path
T.F.
Consider a zero S = -1/Ki to be added to the prototype of second
2
( )
( 2 )
n
G S
S S n
ω
ξω
=
+
Consider a zero S = -1/Ki to be added to the prototype of second
order T.F.
Therefore,
2(1 )
( )
( 2 )
n K S
i
G S
S S n
ω
ξω
+
=
+
2(1 )
( )
2 2 2
( ) 2
2(1 )
( )
2 2 2
( ) (2 )
n K S
Y S i
R S S nS n n K S
i
n K S
Y S i
R S S n n K S n
i
ω
ξω ω ω
ω
ξω ω ω
+
=
+ + +
+
=
+ + +
14-Mar-20 18

19. • Thus, in this case , the effect of adding zero is not only the
term (1 + KiS) appears in the numerator but the denominator
also contains Ki.
• The term (1+KiS) in the numerator increases the Peak
overshoot (Mp) but Ki appearing in the coefficient of ‘S’ term
in denominator has effect of improving the damping or
reducing Mp.
reducing Mp.
14-Mar-20 19

20. Effects of PI Controller
Effects of PI Controller
• Thus, the Integral controller improves the steady state
performance of the system by increasing the type of the system
and reducing the steady state error.
• Increases Rise Time (Ts)
• Decreases Bandwidth (BW)
• Improves GM, PM and Mr
• Improves GM, PM and Mr
• Improves Damping and reduces Maximum Overshoot
14-Mar-20 20

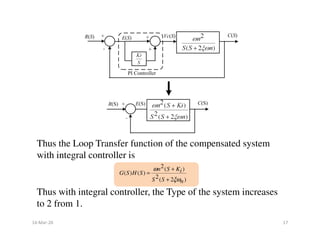
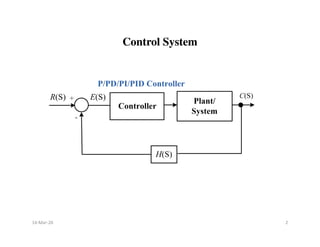
21. Proportional Integral Derivative Controller
(PID Controller)
Proportional Integral Derivative Controller
(PID Controller)
Objective :
1) To improve the Transient and Steady State Response of the
system
PID Controller : In PID Controller, input to the plant is a
combination /sum of three signals. First is the proportional to
the error signal, second is proportional to derivative of error
the error signal, second is proportional to derivative of error
signal and the third is proportional to the integral of error
signal.
[ ( )]
( ) ( ) ( ).
0
( ) ( ) ( ) ( )
d e t
V t e t K K e t dt
c D i
dt
Ki
Vc S E S K S E S E S
D
S
∞
= + + ∫
= + +
Where , KD and Ki = Gains of Derivative and Integral
Controllers, respectively.
14-Mar-20 21

22. 14-Mar-20 22

23. Effects of PID Controller
Effects of PID Controller
• In PID controller, Derivative controller part increases the
damping ratio. This reduces the peak overshoot (%Mp) and
Settling time (Ts) of the system. This reduces the response
time of the system.
• The Integral controller part improves steady state response by
• The Integral controller part improves steady state response by
increasing the type of the system and reducing the steady state
error.
• Hence, PID controller improves the transient as well as steady
state performance of the system.
14-Mar-20 23

24. Design with PD Controller
Design with PD Controller
( )
G S K K S
c p D
= +
Transfer function of the
controller
2
( ) 2 1
R
G S R C S
c
R
= +
( ) 2 1
1
G S R C S
c
R
= +
On Comparison
2
2 1
1
R
Kp KD R C
R
= =
Thus, for Large value of KD, the
capacitor value will be larger
14-Mar-20 24

25. Design with PI Controller
Design with PI Controller
( )
Ki
G S K
c p
S
= +
Transfer function of the
controller
2 2
( )
R R
G S
c
R R C S
= +
( )
1 1 2
G S
c
R R C S
= +
On Comparison
2 2
2
1 1
R R
K K
p i
R R C
= =
Thus, for Small value of Ki , the
capacitor value will be larger
14-Mar-20 25

26. Application
Application
*
T
*
i
bg
ag i
i
bg
agV
V
g
θ
*
*
*
V
V
V
*
*
*
V
V
V
14-Mar-20 26
m
ω
*
e
T
*
qs
i
cs
bs
as i
i
i
0
*
=
ds
i
ds
i
qs
i
*
di
V *
qi
V
bg
ag i
i
*
g
Q
dc
V
*
dc
V
dg
V
5
.
1
−
g
g
θ
r
P λ
5
.
1
1
*
*
*
ci
bi
ai V
V
V
*
*
*
cs
bs
as V
V
V
Controller for Speed and Torque control of Wind Generator
connected to the Grid

27. Thank You ?
Thank You ?
14-Mar-20 27