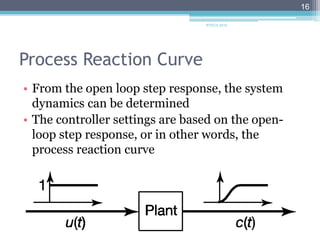
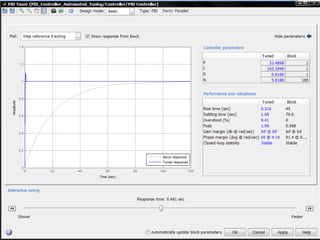
This document discusses various empirical techniques for tuning PID controllers, including the Ziegler-Nichols and Cohen-Coon reaction curve methods. The Ziegler-Nichols method determines controller parameters by forcing sustained oscillations and measuring the ultimate gain and period. The Cohen-Coon method analyzes the open-loop step response curve to estimate parameters. Simulation tools can also assist in empirically tuning controllers to achieve desired closed-loop responses.

1. Tuning PID Controllers
Eng. Mahmoud Hussein
RTECS 2010
1
RTECS 2010
1
Gc(s)
Controller
+
+ n
sensor
noise
+
w load disturbance
+
Gp(s)
Plant
u
control
y
output
+
-
r
reference
input, or
set-point
e
sensed
error

2. RTECS 2010
2

3. Analytical Vs. Empirical Techniques
• Analytical Tuning Techniques
▫ Frequency response analysis
• Empirical Tuning Techniques
▫ On-line tuning after the control system is installed
▫ Computer simulation
RTECS 2010
3

4. Empirical Tuning Techniques
• Two Steps:
▫ Determination of the dynamic characteristics of
the control loop
▫ Estimation of the controller tuning parameters
that produce a desired response
• Tuning Techniques
▫ Ziegler-Nichols Oscillation Method
▫ Ziegler-Nichols Reaction Curve Method
▫ Cohen-Coon Reaction Curve Method
RTECS 2010
4

5. Z-N Closed Loop Method
Z-N Continuous Cycling Method
By Ziegler and Nichols (1942)
RTECS 2010
5

6. Quarter Decay Ratio Response By
Ultimate Gain
• Use the proportional controller to force
sustained oscillations.
• Goal is to determine ultimate gain and ultimate
period of oscillation of the control loop
RTECS 2010
6

7. Quarter Decay Ratio Response By
Ultimate Gain
• Ziegler-Nichols method specifies a decay ratio of
one-fourth (1/4)
• Decay ratio = ratio of the amplitudes of two
successive oscillations
RTECS 2010
7

8. Tuning Procedure
• Set the true plant under proportional control,
with a very small gain
• Increase the gain until the loop starts oscillating
▫ Note that linear oscillation is required and that it
should be detected at the controller output.
• Record the controller critical gain (ultimate
gain) Kp = Kc (Ku) and the oscillation period of
the controller output, Pc (Pu).
RTECS 2010
8

9. Tuning Procedure
• Calculate the parameters according to the
following formulas
RTECS 2010
9
Controlle
r Type
Proportional
Gain (Kp)
Integral
Time (tI)
Derivative
Time (tD)
P-only Ku/2 - -
PI Ku/2.2 Pu/1.2 -
PID Ku/1.7 Pu/2 Pu/8

10. Example
• Consider the given plant
▫ Find the parameters of a PID controller using the
Z-N oscillation method.
▫ Obtain a graph of the response to a unit step input
reference.
RTECS 2010
10
 3
1
1
)(
+

s
sGp

11. Example Solution
• Applying the procedure we find
▫ Kc = 8 and ωc = 3
• Hence, from Table we have
▫ Kp = 4.8
▫ Tr = 1.81
▫ Td = 0.45
• Try the same procedure for the second order
system
RTECS 2010
11
 2
1
1
)(
+

s
sGp

12. Drawbacks
• Time-consuming
▫ If the process dynamics are slow
• The process is pushed to the stability limits
▫ Risk of plant damage
• For first-order and second-order model without
time delays the ultimate gain does not exist
▫ Because the closed-loop system is stable for all
values of Kp. However, in practice, it is unusual
for a control loop not to have an ultimate gain.
RTECS 2010
12

13. RTECS 2010
13

14. Tuning Procedure
• Same procedure as Z-N closed loop method
• TLC tuning values tend to reduce oscillatory
effects and improves robustness.
RTECS 2010
14

15. Z-N Open-loop Method
RTECS 2010
15

16. Process Reaction Curve
• From the open loop step response, the system
dynamics can be determined
• The controller settings are based on the open-
loop step response, or in other words, the
process reaction curve
RTECS 2010
16

17. Tuning Procedure
• With the plant in open loop, take the plant
manually to a normal operating point
▫ Say that the plant output settles at y(t) = y0 for a
constant plant input u(t) = u0.
• At an initial time, t0, apply a step change to the
plant input, from u0 to u
▫ This should be in the range of 10 to 20% of full
scale
• Record the plant output until it settles to the
new operating point. Assume you obtain the
curve shown on the next slide.
RTECS 2010
17

18. Tuning Procedure
RTECS 2010
18
• Compute the parameter model as follows
m.s.t. stands for maximum slope
tangent

19. RTECS 2010
19

20. Tuning Procedure
• Cohen and Coon carried out further studies to
find controller settings which, based on the same
model, lead to a weaker dependence on the ratio
of delay to time constant. Their suggested
controller settings are shown below
RTECS 2010
20

21. Simulink Control Design 3.0
RTECS 2010
21

22. PID Controller Block
▫ PID_Controller_Automated_Tuning.mdl
RTECS 2010
22

23. Initial PID Design
RTECS 2010
23

24. Adjusting Response Time To Tune
Parameters
RTECS 2010
24