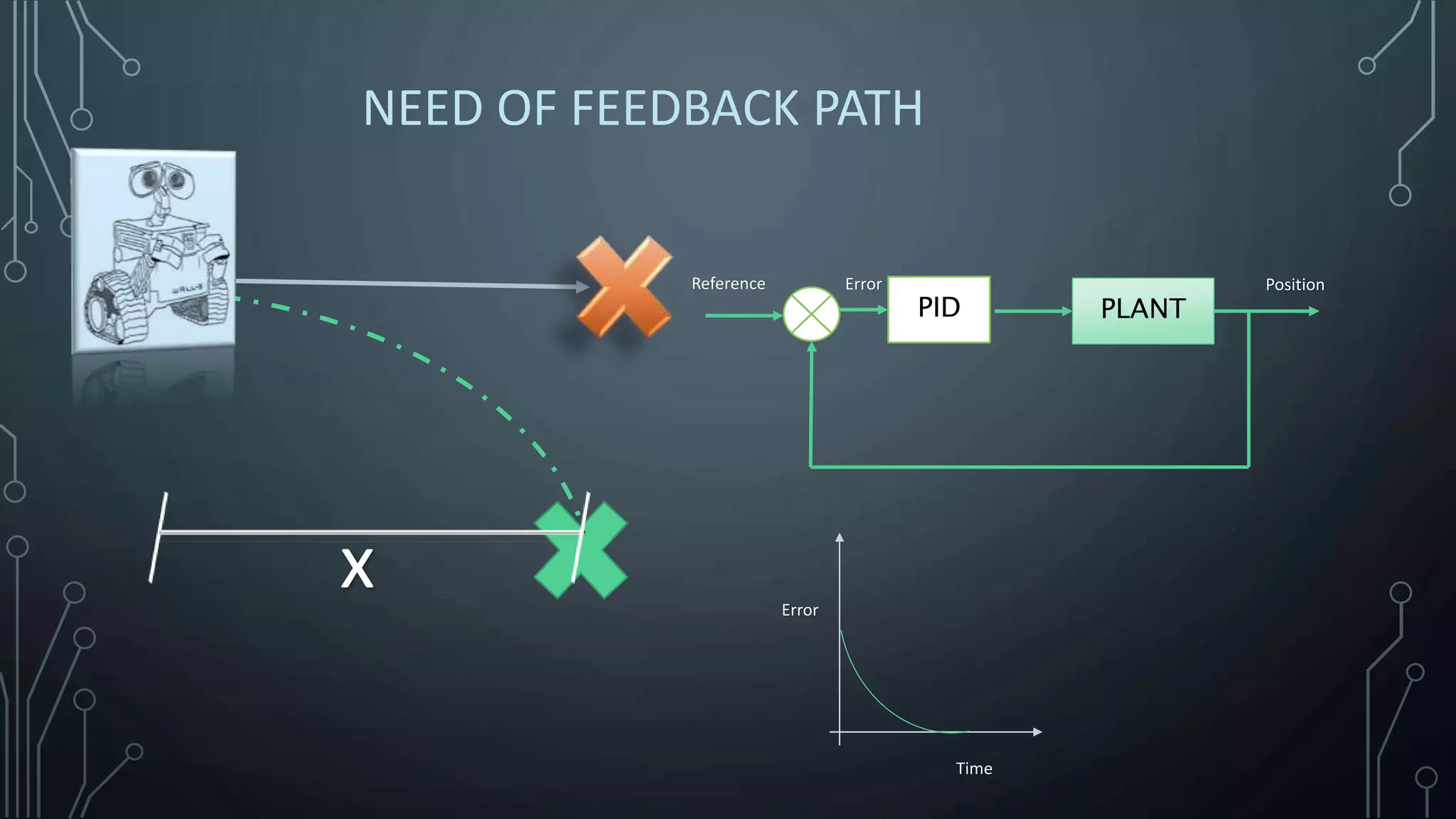
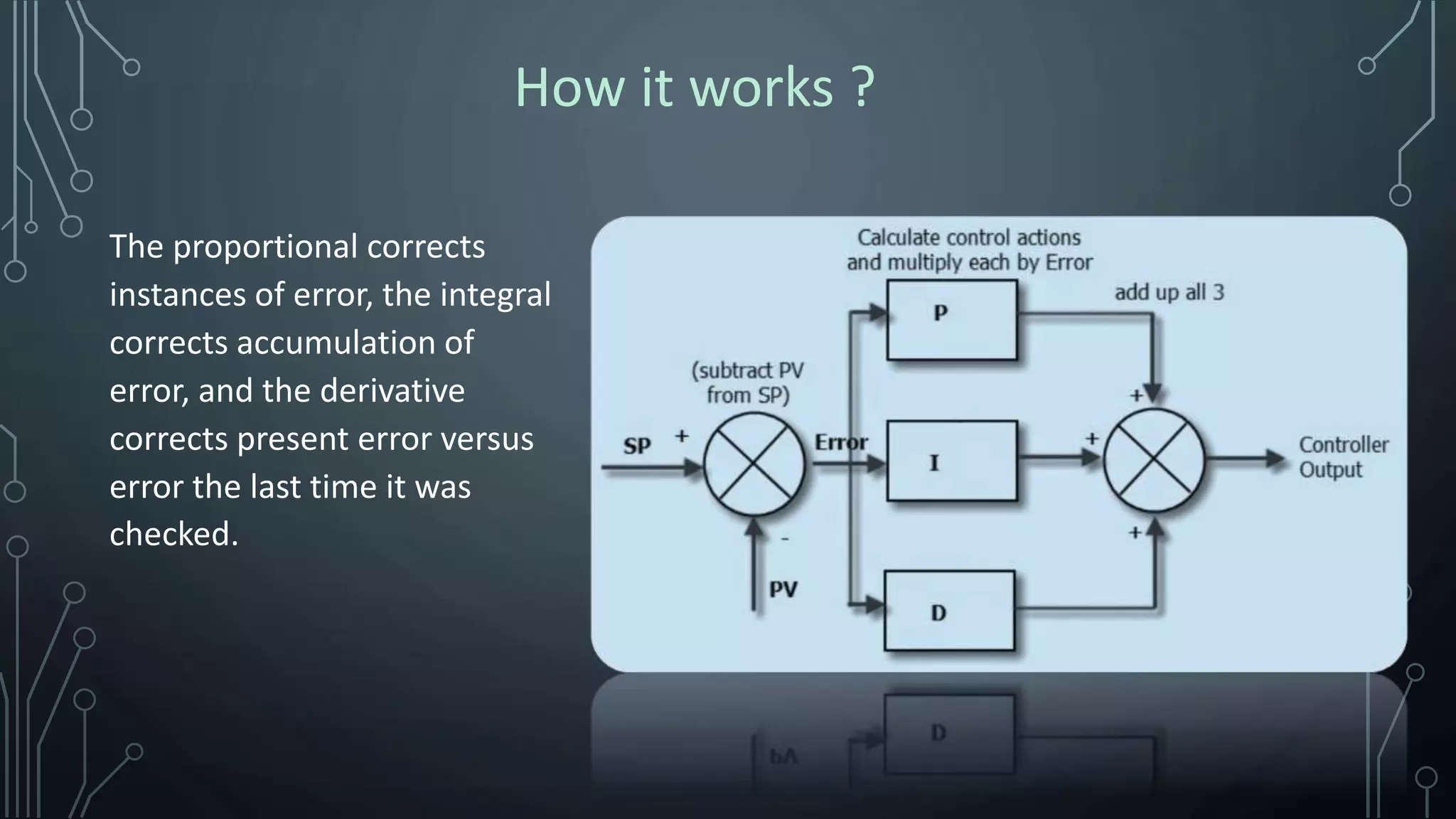
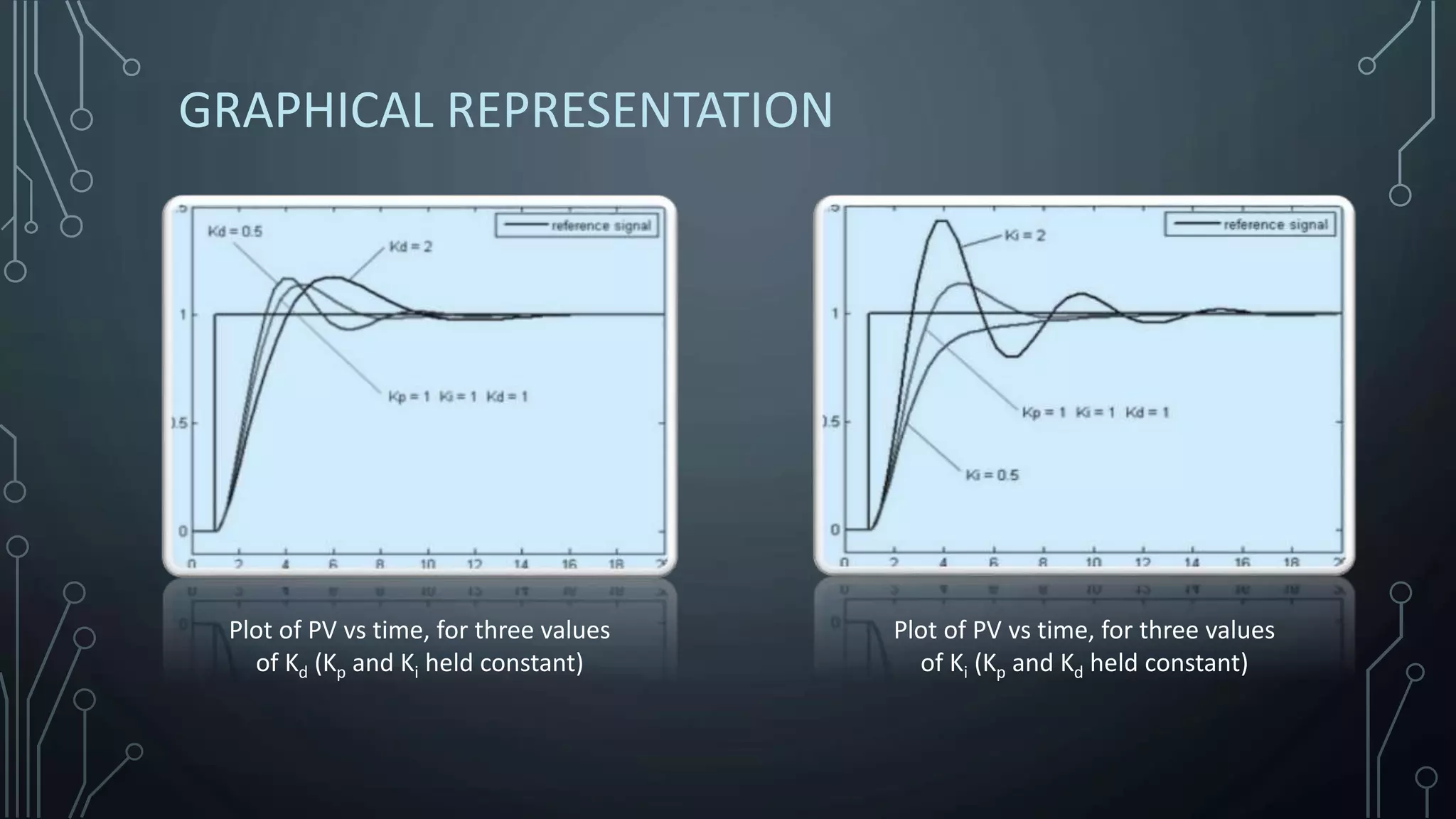
The document explains the concept of PID (Proportional, Integral, Derivative) controllers, emphasizing their role in reducing errors in control systems through feedback mechanisms. It details how each term of the PID controller functions and highlights its widespread industrial application, where over 95% of controllers are of this type. Examples of applications include temperature control, chemical reactors, and automation in various technologies.

1. P.I.D. CONTROLLER
BY NAYAN SHREE
DEPARTMENT OF ELECTRICAL ENGINEERING
ROLL NO:- 15/EE/69
HALDIA INSTITUTE OF TECHNOLOGY

2. WHAT IS P.I.D. ?
• PID stands for Proportional(P) Integral(I) Derivative(D).
• It is a Control Loop Feedback Mechanism, which is used to reduce the errors
produced in a control system.
• It helps in continuous modulated control, which calculates the error that is
equal to the difference between Process Variable and Setpoint(Reference
Value) and helps to regulate the desired output what us set by us as a
reference point.

3. NEED OF FEEDBACK PATH
x
PID PLANT
Reference Error Position
Error
Time

4. The proportional corrects
instances of error, the integral
corrects accumulation of
error, and the derivative
corrects present error versus
error the last time it was
checked.
How it works ?

5. PROPORTIONAL TERM
• The Proportional term makes the value of current error multiplied by a gain(Kp), thus the
result will be the output signal of the gain and the error.
• Output signal will be = Kp * e(t), where e(t) is the error in time t.
• From this curve we can see that when the error is large the proportional path will produce
large outputs, when error is zero the output is zero and when the error is negative the
output will be negative.
Error
Time

6. INTEGRAL TERM
• The integral makes the current error signal value and duration multiplied
with a gain(Ki).
• The Output signal comes out to be = Ki
𝟎
𝒕
𝒆 𝒕 𝒅𝒕.
• Integral signal is sum of all instantaneous values, so when integral and
proportional terms are added the movement get accelerated towards the
setpoint.

7. DEREVATIVE TERM
• Derivative term is the instantaneous value of the error at a particular
moment multiplied with a gain(Kd).
• So the output signal comes out to be = Kd
𝒅
𝒅𝒕
e(t).
• Derivative term slows the rate of change of the controller output.

8. • PID is simple, efficient, and effective, so from the earlier ages it is considered as the
best controller.
• More than 95% of the industrial controllers are of PID type, the output of the PID
controller u(t) can be expressed in terms of the input e(t), as:
WHY PID?

9. GRAPHICAL REPRESENTATION
Plot of PV vs time, for three values
of Ki (Kp and Kd held constant)
Plot of PV vs time, for three values
of Kd (Kp and Ki held constant)

10. APPLICATIONS
• Temperature Control using a Digital PID controller
• Chemical Reactors
• Self balancing robot
• Line following bot
• Auto balancing of a multirotor flying machine
• Auto driving vehicles for roads
• Home automation and control
• Automatic power control in substations

11. References :- Wikipedia, NPTEL, google