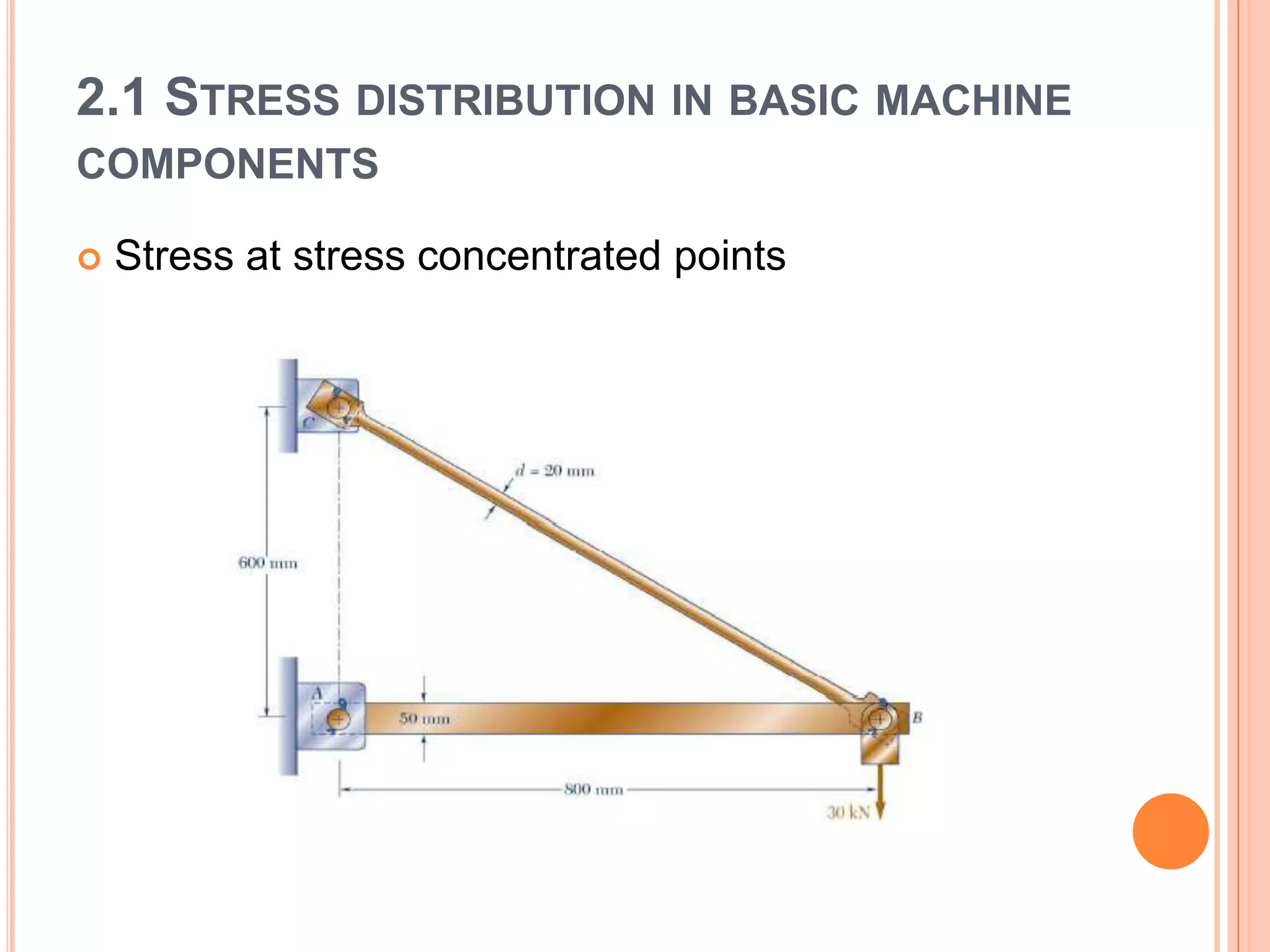
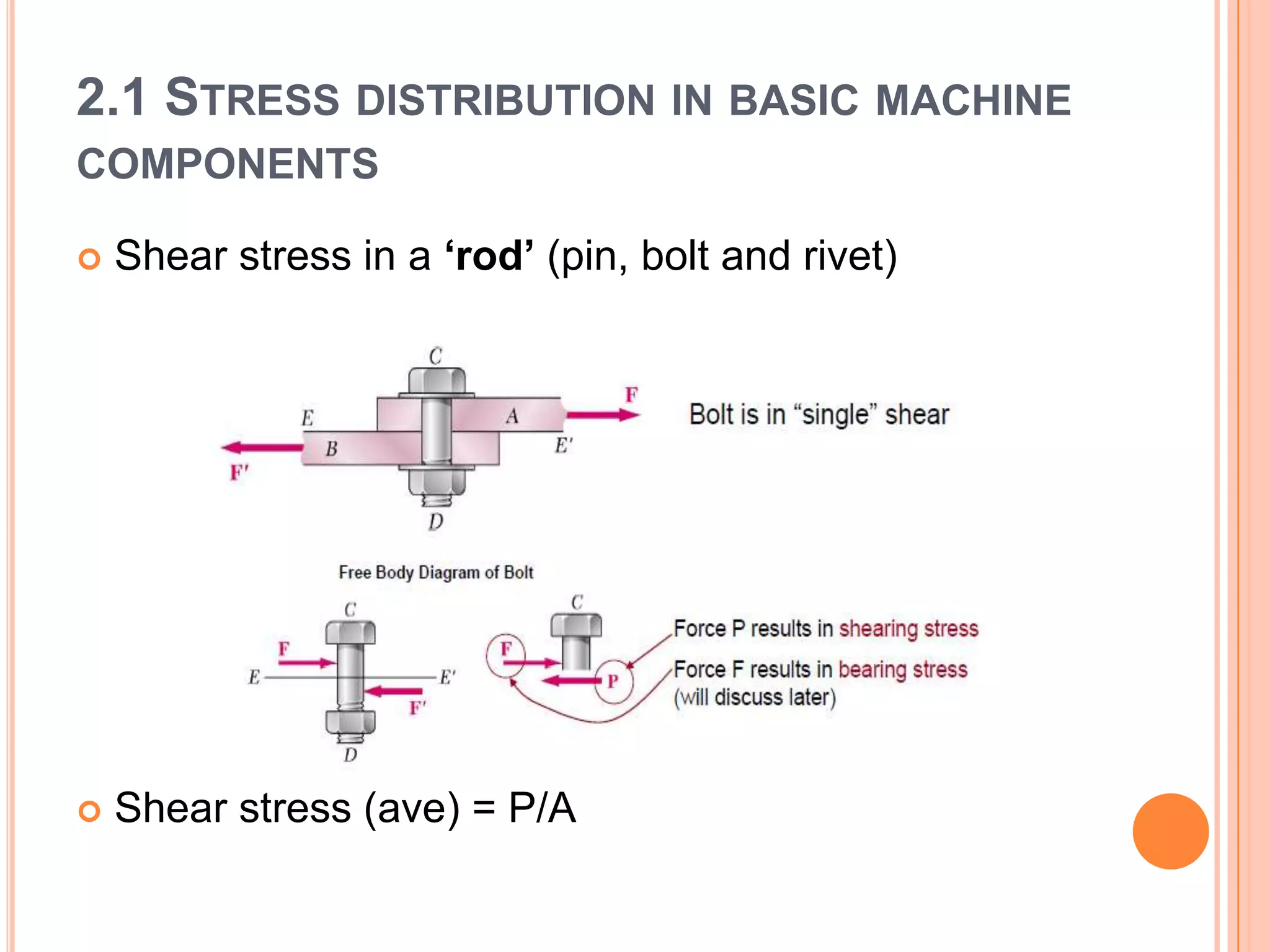
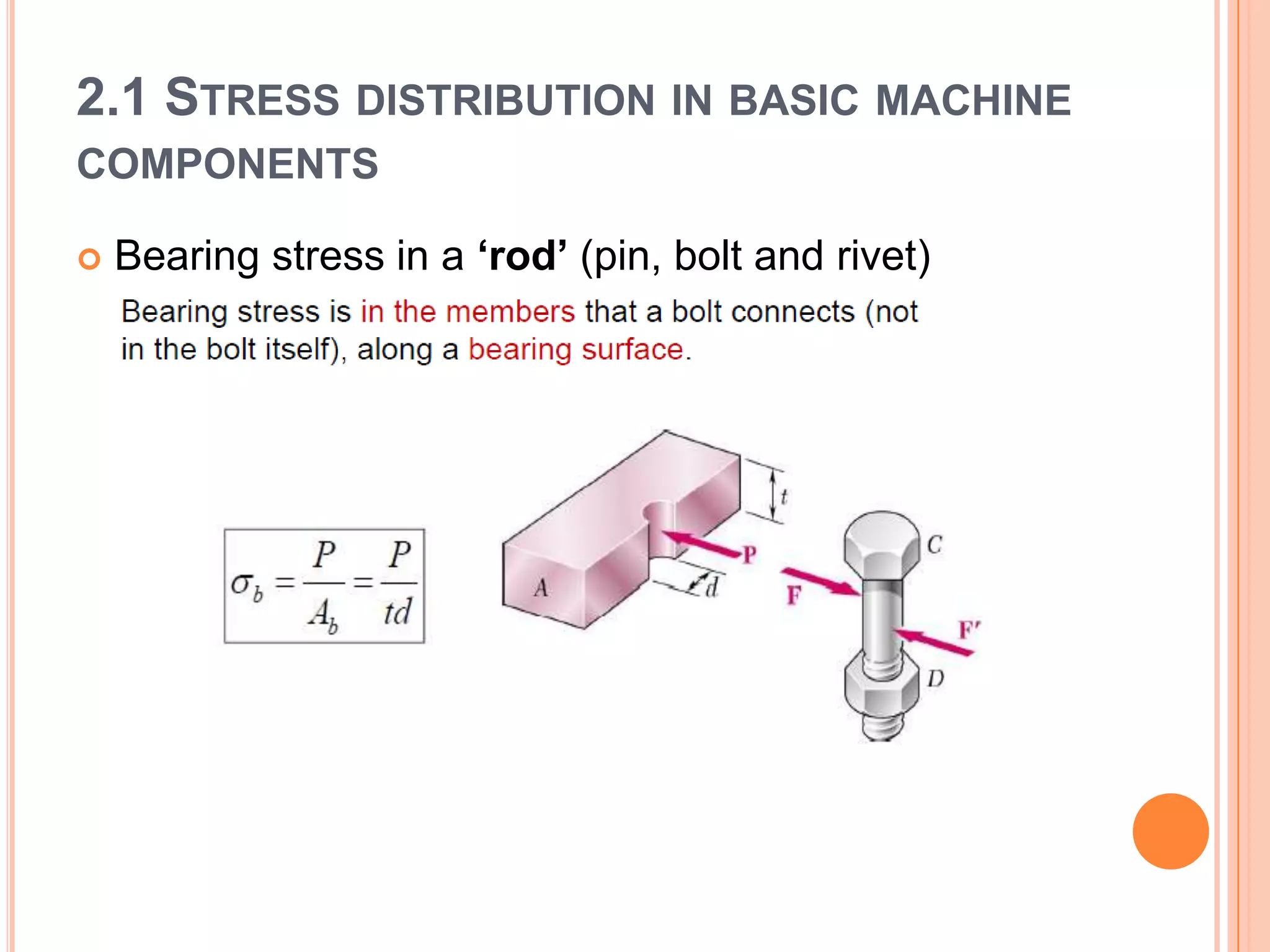
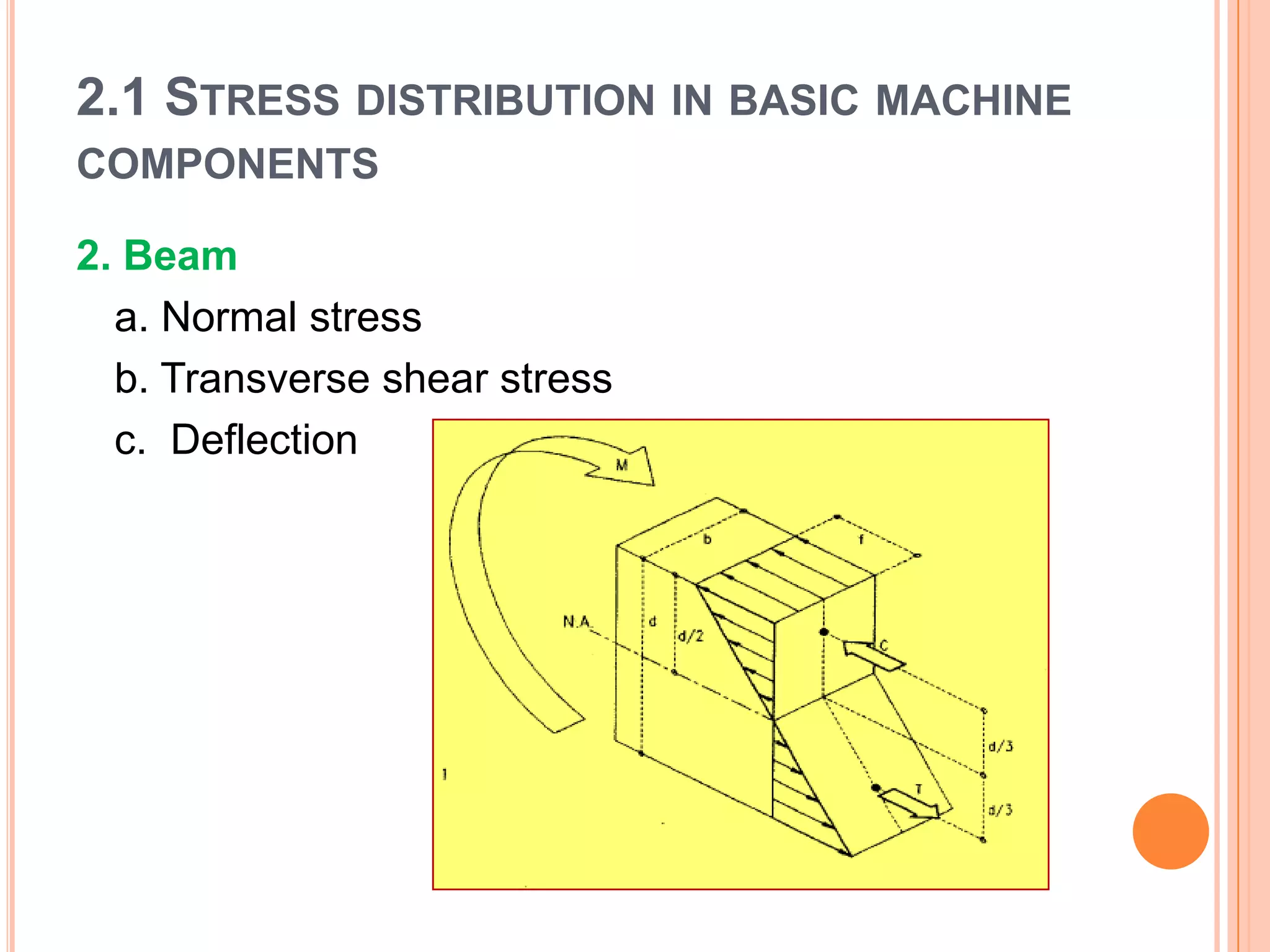
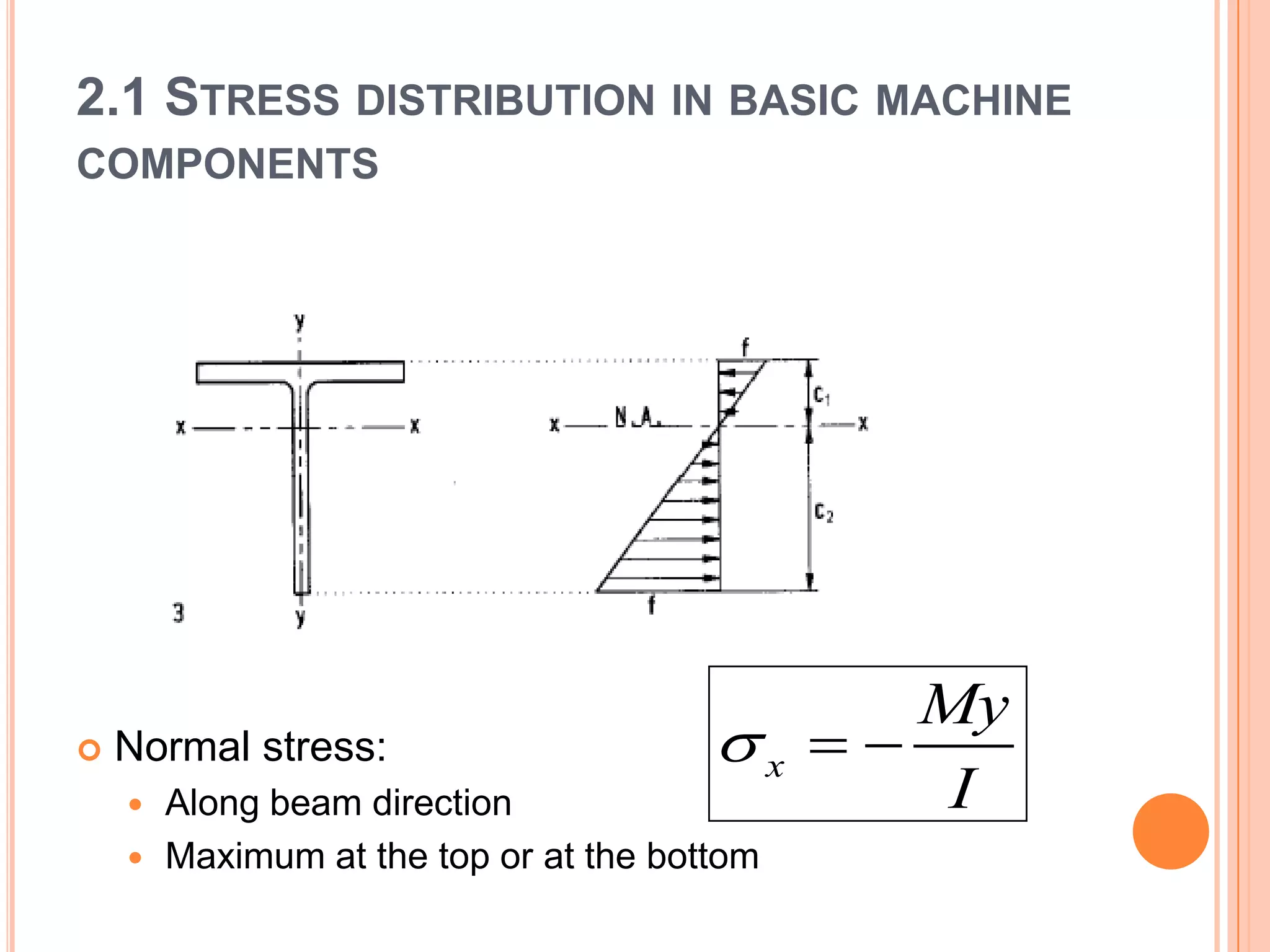
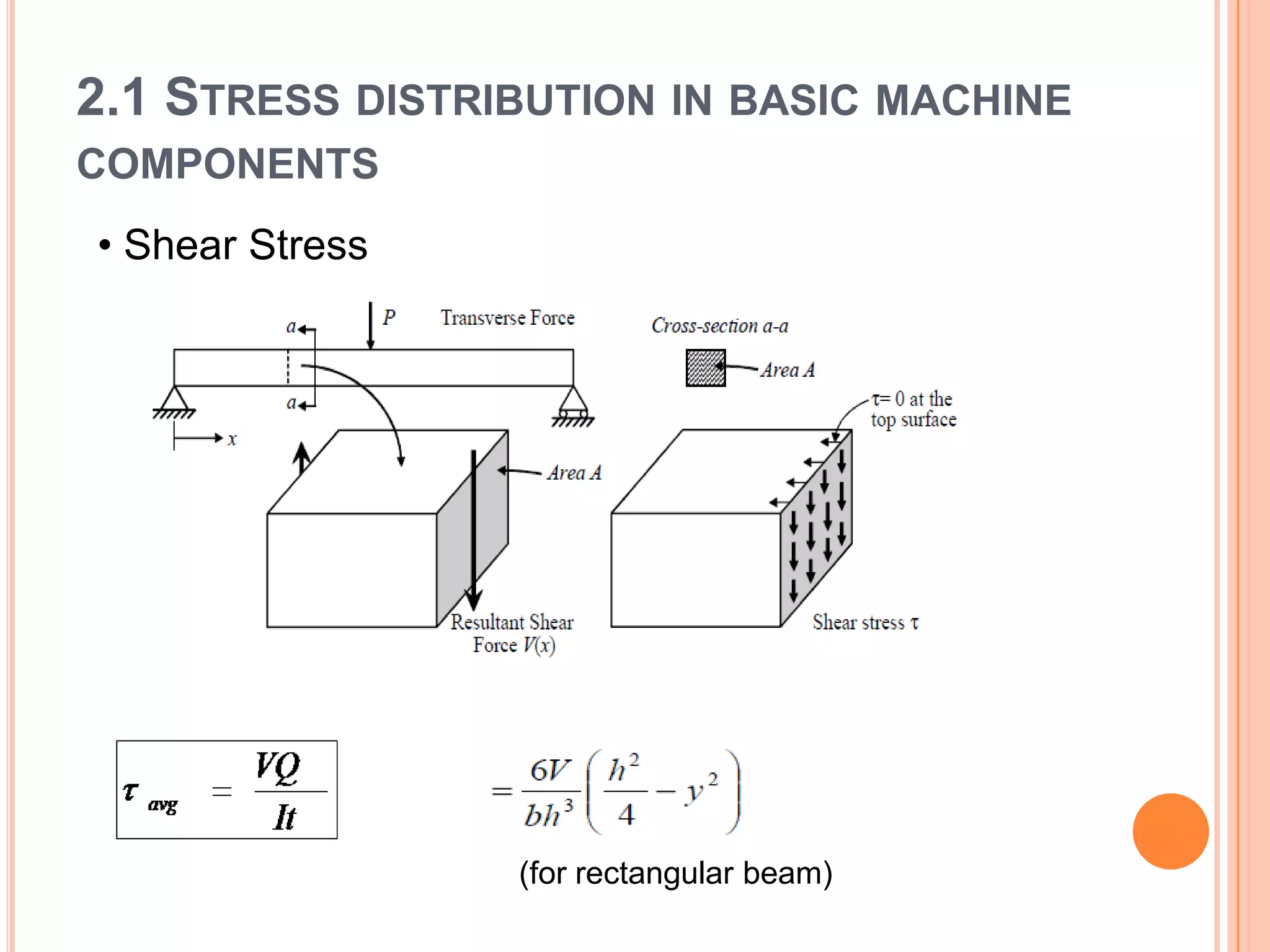
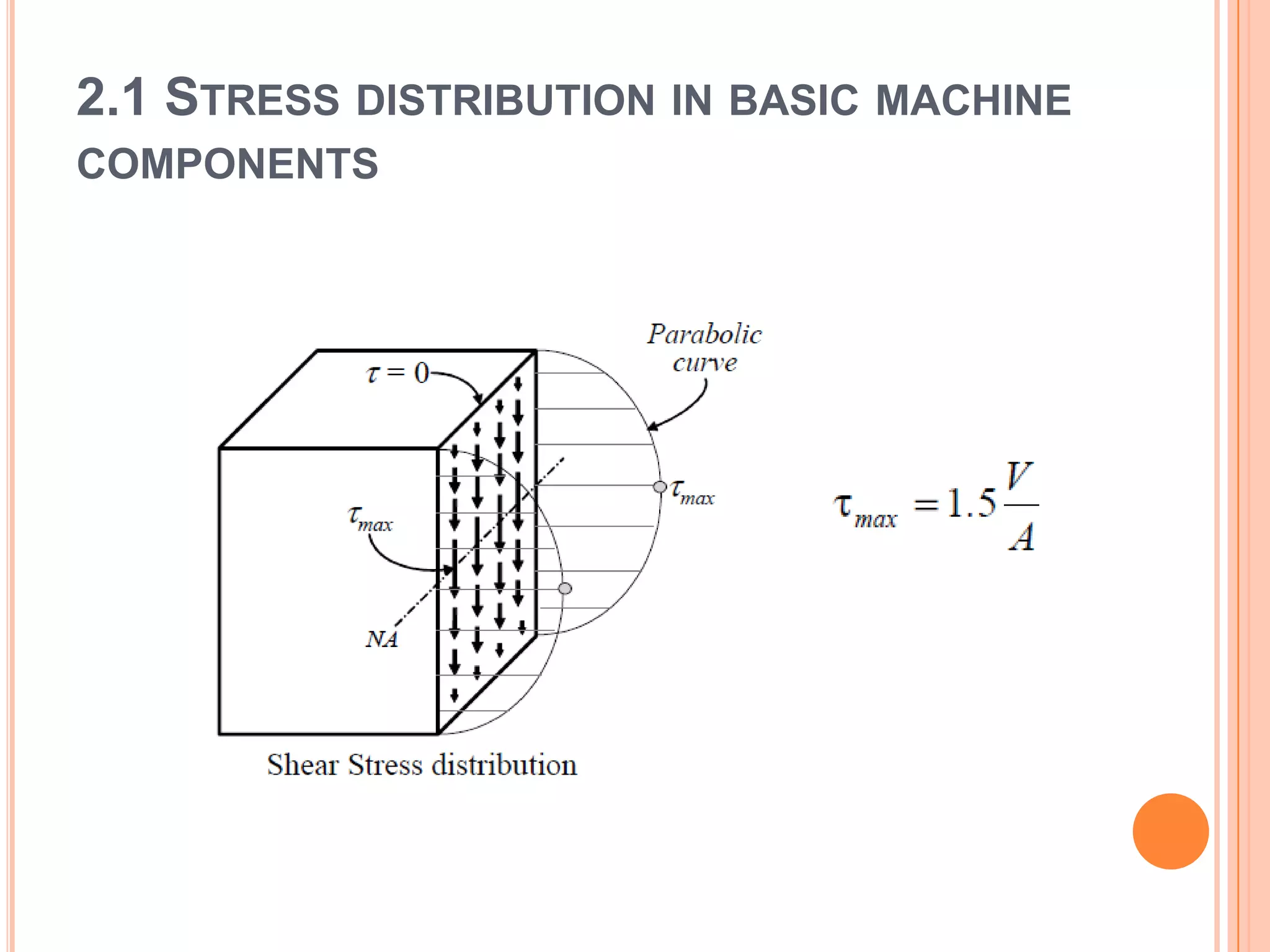
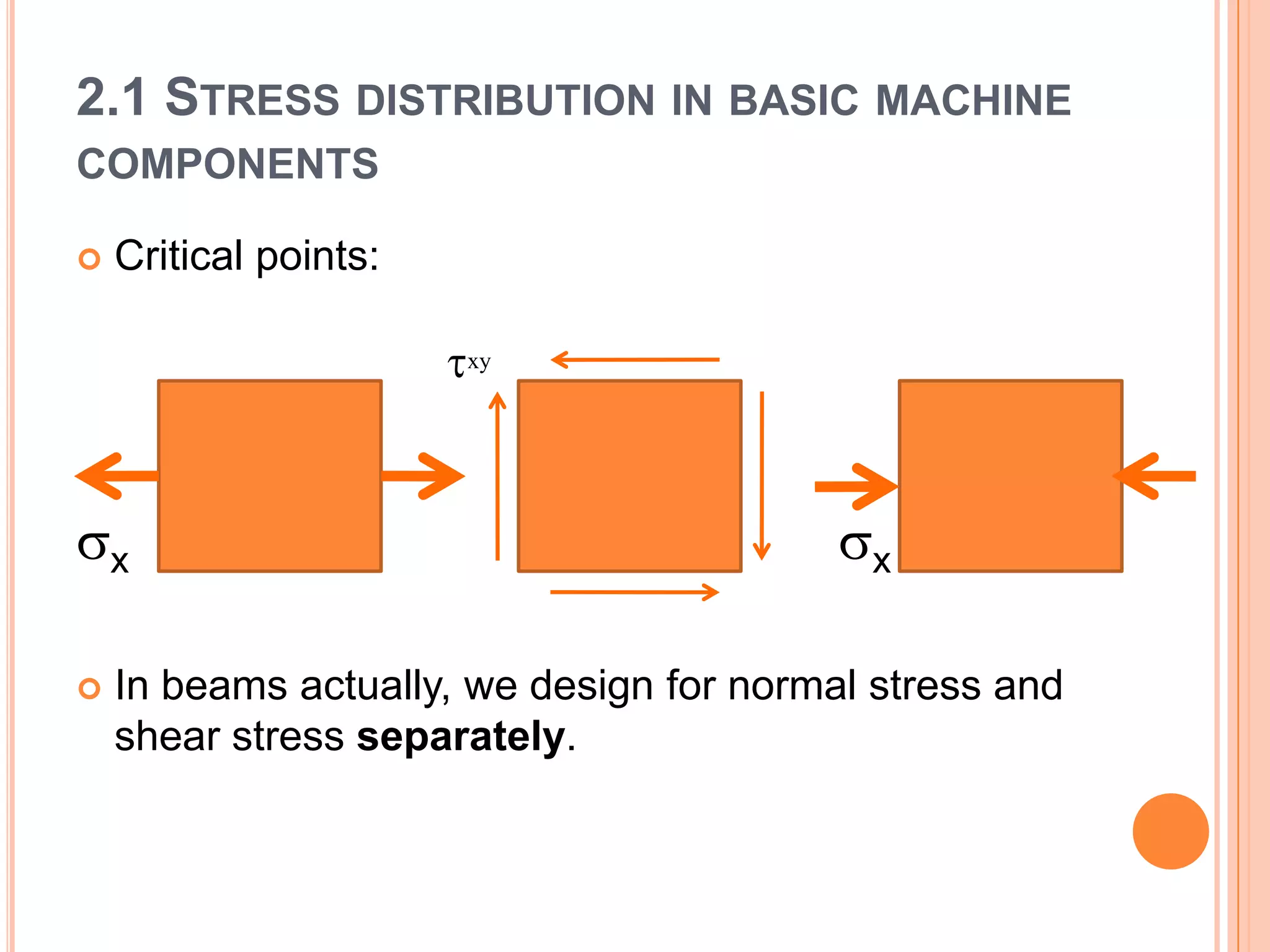
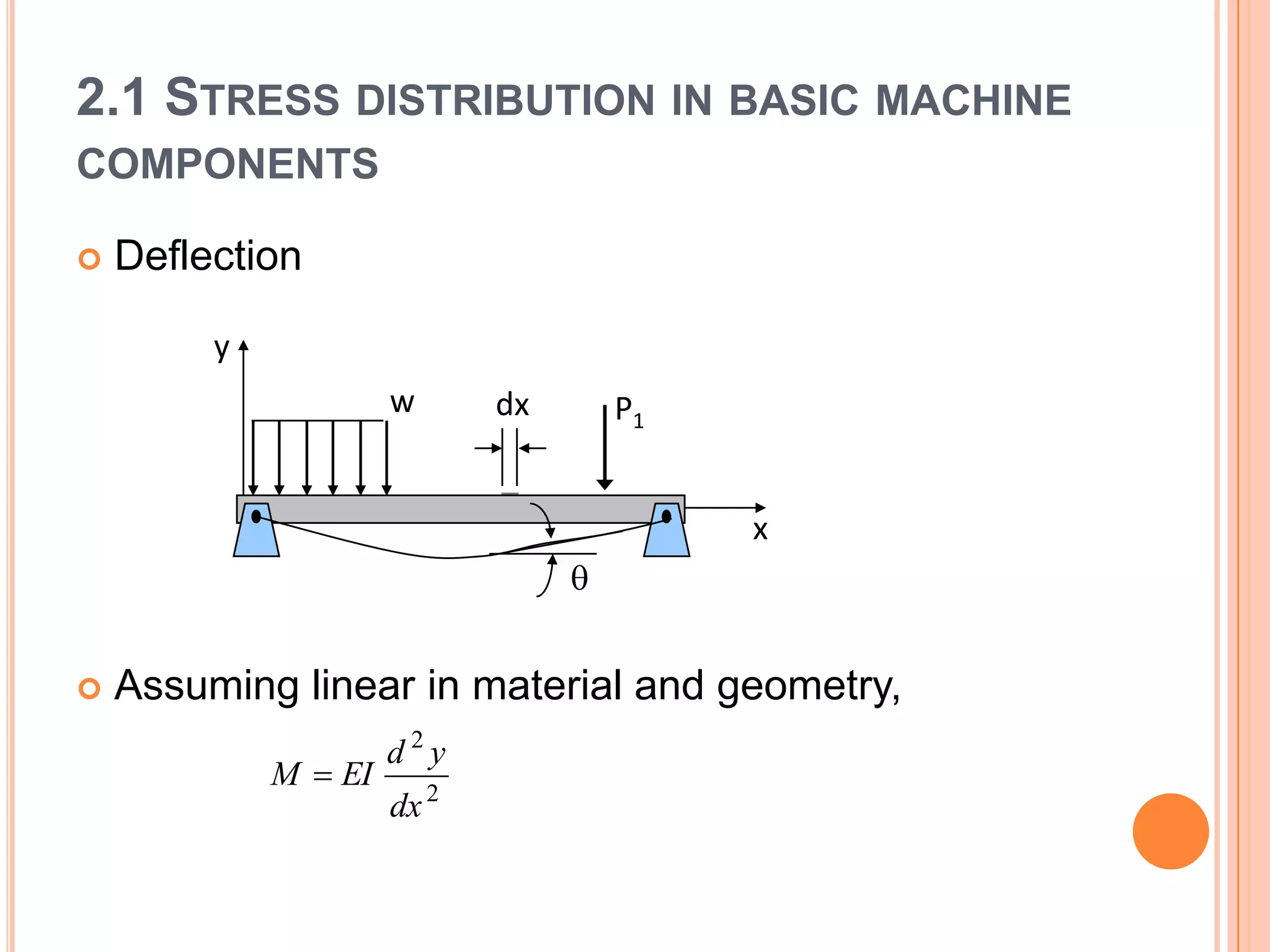
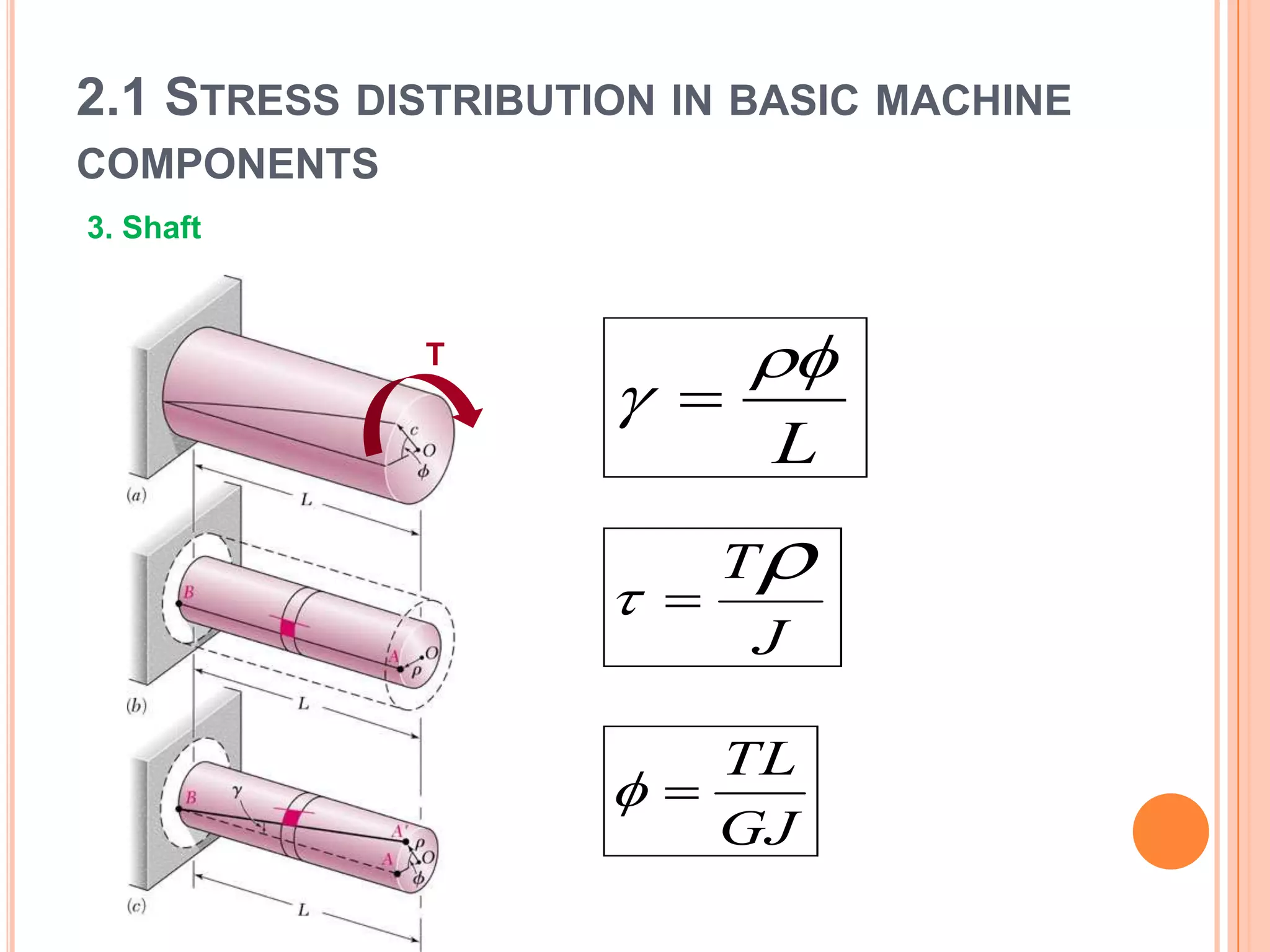
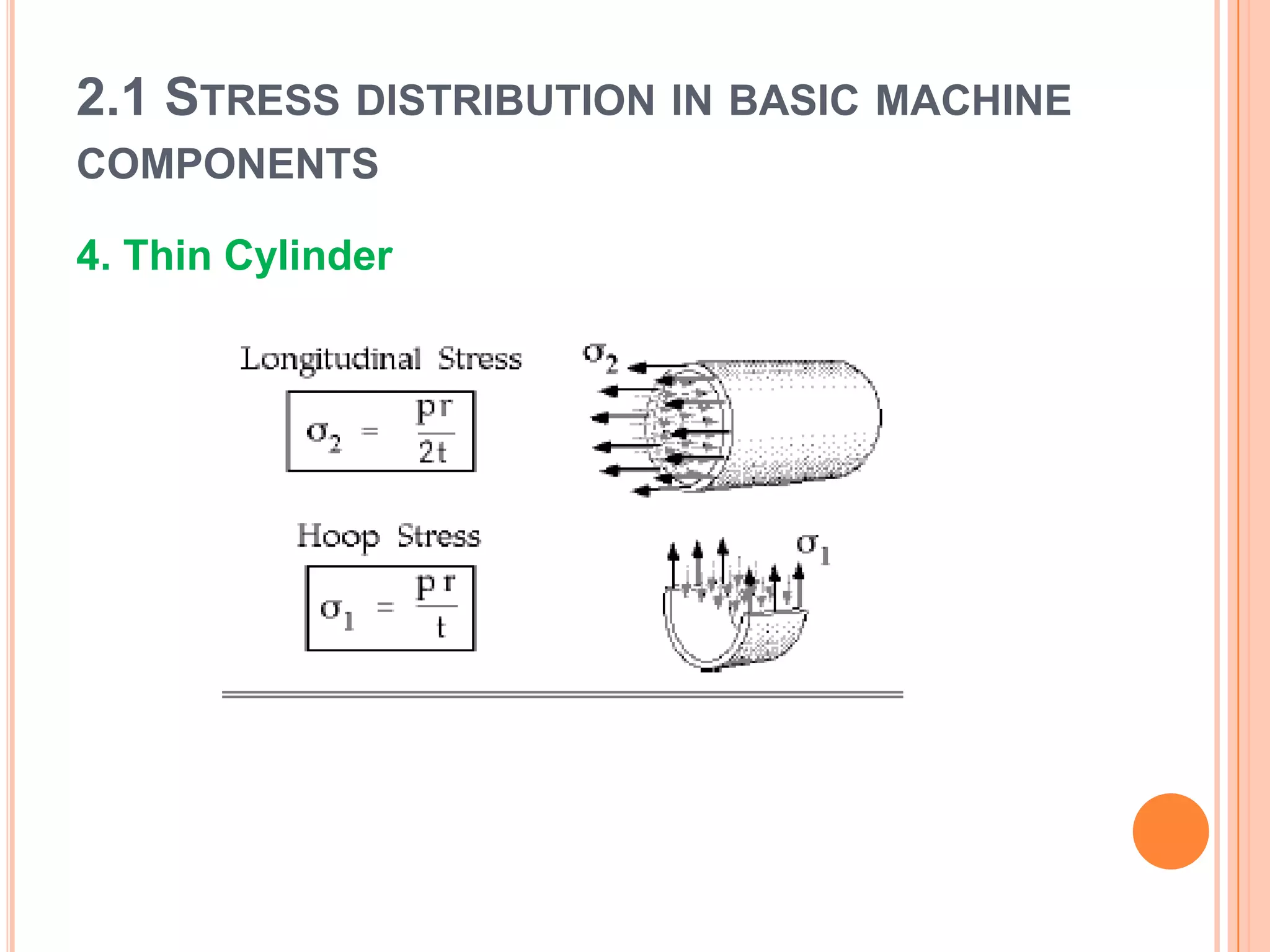
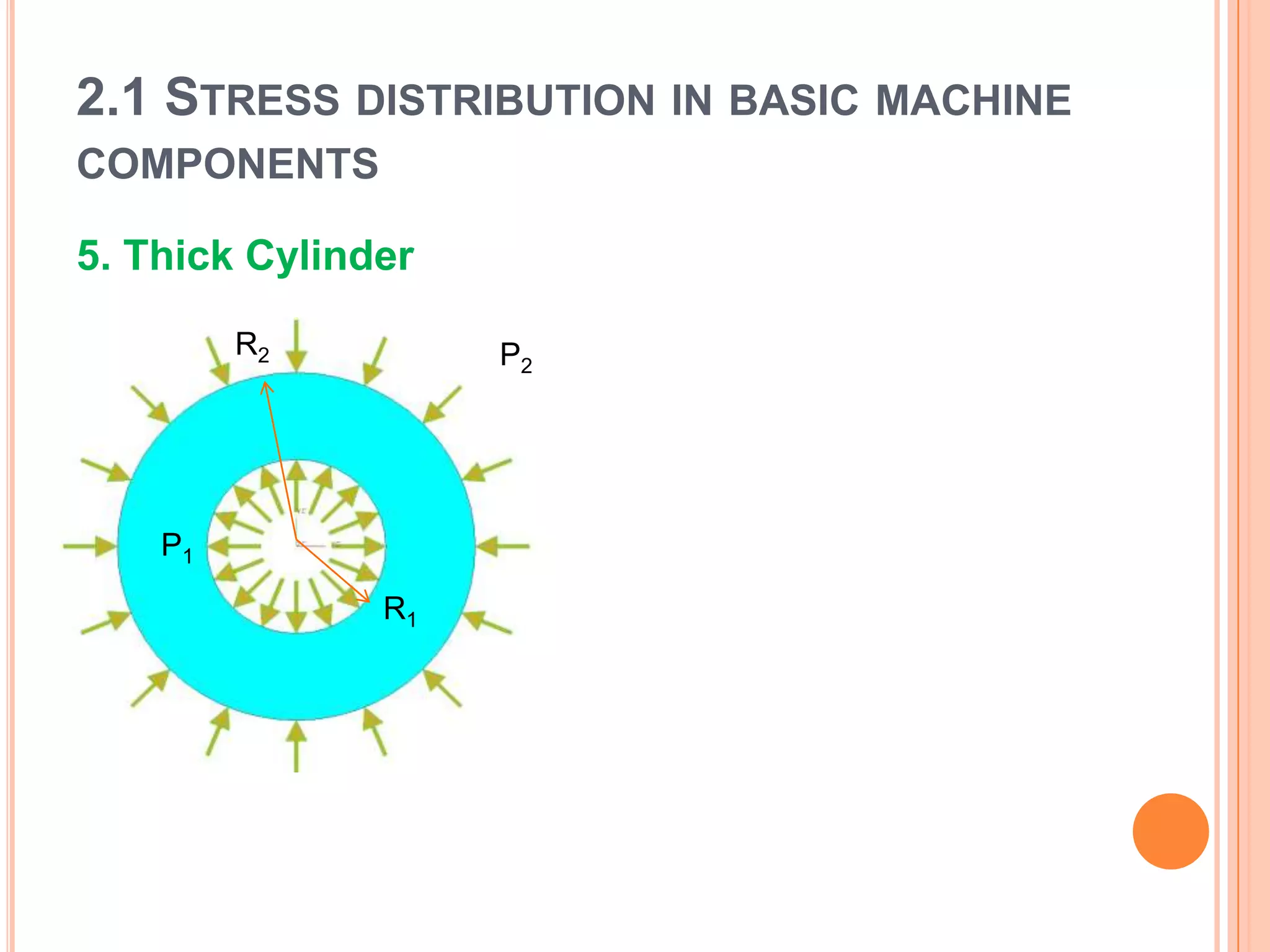
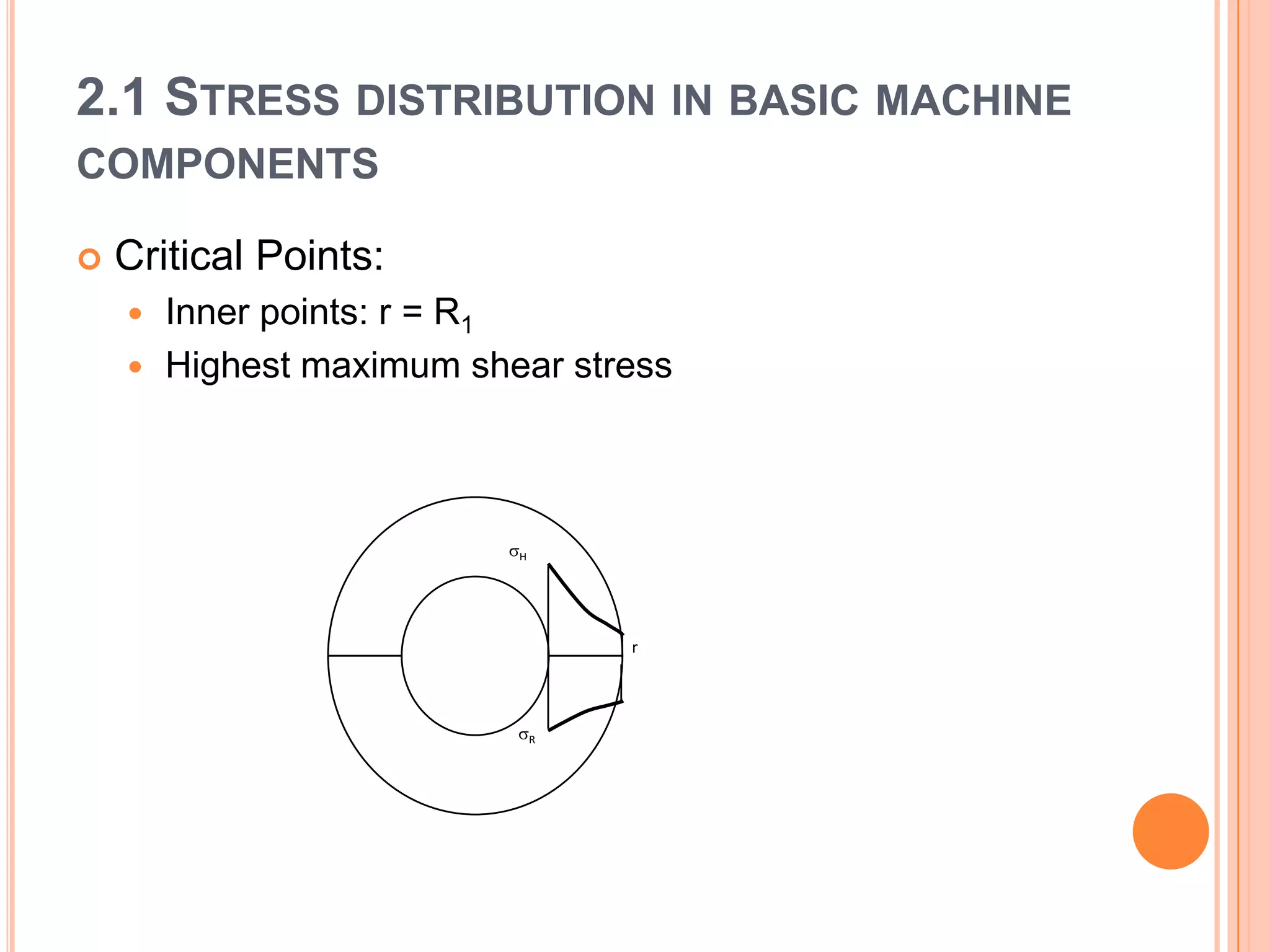
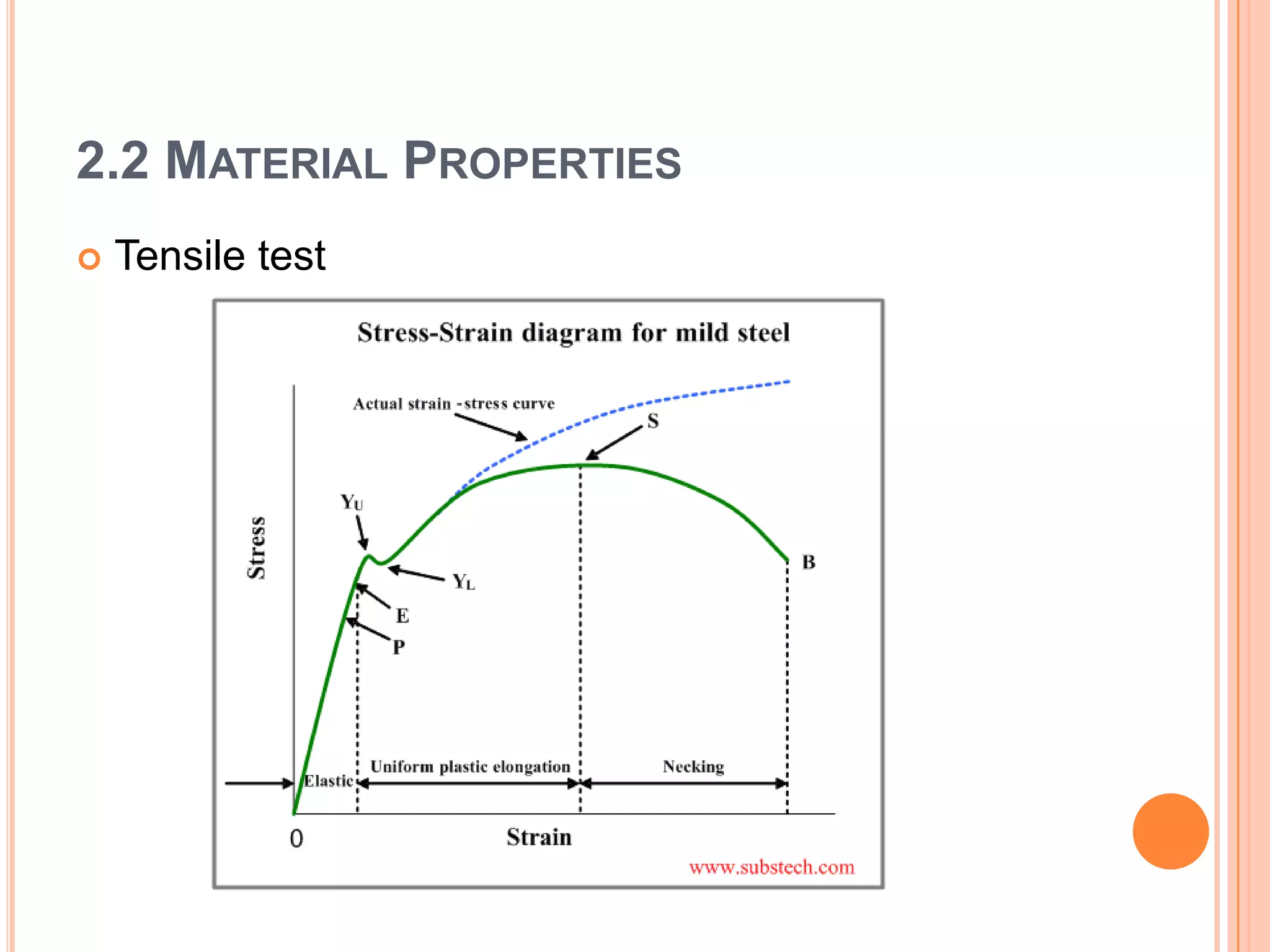
The document discusses stress distribution in basic machine components such as rods, beams, shafts, thin cylinders, and thick cylinders. It describes the different types of stresses that act on these components, including normal stress, shear stress, bearing stress, and deflection. The key points covered are the stress concentration at critical points, the formulas used to calculate stresses, and the factors considered in the design of these components for both stress and strength.

1. CHAPTER 2 : STATIC LOADING

2. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
1. Rod
 Critical point (in general): Any point
 Critical point (specifically): At stress cncentrated
points

3. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
 Stress at stress concentrated points

4. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
 Shear stress in a ‘rod’ (pin, bolt and rivet)
 Shear stress (ave) = P/A

5. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
 Bearing stress in a ‘rod’ (pin, bolt and rivet)

6. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
2. Beam
a. Normal stress
b. Transverse shear stress
c. Deflection

7. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
 Normal stress:
 Along beam direction
 Maximum at the top or at the bottom
x
My
I
  

8. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
(for rectangular beam)
• Shear Stress

9. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS

10. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
 Critical points:
 In beams actually, we design for normal stress and
shear stress separately.
x x
xy

11. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
 Deflection
 Assuming linear in material and geometry,
P1
x
y
w dx

2
2
dx
yd
EIM 

12. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
 Design of beams
 Prismatic design:
 Design for normal stress
Sreqd = Required section modulus
For long beam.
 Design for shear stress
For short beam with concentrated load
Especially for wood beam
 Fully stressed beam design

13. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
T
L

 
GJ
TL

J
T 
3. Shaft

14. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
4. Thin Cylinder

15. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
5. Thick Cylinder
P2
P1
R2
R1

16. 2.1 STRESS DISTRIBUTION IN BASIC MACHINE
COMPONENTS
 Critical Points:
 Inner points: r = R1
 Highest maximum shear stress
r
H
R

17. 2.2 MATERIAL PROPERTIES
 Basic material properties:
 Physical: Density
 Mechanical:
 Young’s modulus
 Shear modulus
 Yield strength
 UTS
 Elongation at break
 Reduction of area
 Poisson’s ratio
 Toughness: modulus of toughness, modulus of resilience
 Hardness (Brinnel, Rockwell, Vickers)
 Impact strength (Izod, Charpy)
 Test:
 Tensile test
 Hardness test
 Impact test

18. 2.2 MATERIAL PROPERTIES
 Tensile test

19. 2.2 MATERIAL PROPERTIES
 Standard codes
1. Society of Automotive Engineers (SAE)
2. British Standards (BS)
3. European standards – (EN)
4. ASTM (UNS)
5. Japanese Industrial Standards (JIS)
6. Germany steel grades (DIN)
7. China steel grades (GB)

20. 2.2 MATERIAL PROPERTIES
 Determine the alloy
content, properties, applications and its code
number.
1. Cast Iron
2. Carbon Steel & Alloys
3. Stainless Steel & Alloys
4. Aluminum & Alloys
5. Magnesium & Alloys
6. Copper &Alloys
7. Titanium & Alloys
8. Zircanium & Alloys
9. Nickel & Alloys
10. Zinc & Alloys

21. 2.3 FAILURE THEORY
 To develop FS of the design
 Static failure theory
 Tresca’s theory
 von Misses’s theory

22. 2.3 FAILURE THEORY
1 1.25 - 1.5
for exceptionally reliable materials used under controllable
conditions and subjected to loads and stresses that can be
determined with certainty - used almost invariably where low
weight is a particularly important consideration
2 1.5 - 2 for well-known materials under reasonably constant environmental
conditions, subjected to loads and stresses that can be determined
readily.
3 2 - 2.5
for average materials operated in ordinary environments and
subjected to loads and stresses that can be determined.
4 2.5 - 3 for less tried materials or for brittle materials under average
conditions of environment, load and stress.
5 3-4 for untried materials used under average conditions of
environment, load and stress.
6 3-4 should also be used with better-known materials that are to be used
in uncertain environments or subject to uncertain stresses.
7
Repeated loads : the factors established in items 1 to 6 are
acceptable but must be applied to the endurance limit (ie. a fatigue
strength ) rather than to the yield strength of the material.
8 Impact forces : the factors given in items 3 to 6 are acceptable, but
an impact factor (the above dynamic magnification factor )
should be included.
9 Brittle materials : where the ultimate strength is used as the
theoretical maximum, the factors presented in items 1 to 6 should
be approximately doubled.
10 Where higher factors might appear desirable, a more thorough
analysis of the problem should be undertaken before deciding on
their use.
based on yield strength - according to Juvinall & Marshek op cit.