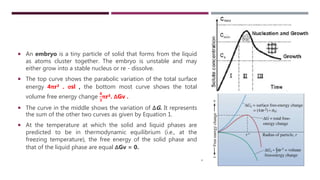
The lecture focuses on the solidification process of metals and alloys, emphasizing nucleation and growth mechanisms including homogeneous and heterogeneous nucleation, as well as planar and dendritic growth. It covers critical concepts such as critical radius for nucleation, cooling curves, and the factors affecting solidification time. By the end of the lecture, students should understand the nucleation process and differences between growth types, supported by calculations of critical radius and examples from cooling curves.

1. LECTURE 8
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 1

2. TOPICS DISCUSSED IN LAST LECTURE
 Solidification
 Cooling Curves of Metal and Alloy
 Solidification Mechanism
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 2

3. TOPICS TO BE DISCUSSED IN TODAY’S LECTURE
 Nucleation
 Homogeneous and Heterogeneous Nucleation
 Critical Radius for Nucleation and its derivation
 Planar and Columnar Growth
 Solidification Time
 Problems based on critical radius and cooling curves
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 3

4. LECTURE OBJECTIVE
At the end of this lecture, one should be able to:
i. Understand the Nucleation Process
ii. Difference between Homogeneous and Heterogeneous Nucleation
iii. Understand difference between planar growth and dendritic growth
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 4

5. NUCLEATION
 This is the starting point of the solidification process of any metal or alloy.
 In a broader sense, the term nucleation refers to the initial stage of formation of one phase from another
phase.
 In this stage, a number of minute crystals nucleate through out the melt.
 Metal in molten state possesses high energy and atoms are in random state.
 As the metal cools, atoms gradually loose their energy and start colliding with each other.
 During these collisions, energy is released out and attractive forces are set up between them.
 These attractive forces result in formation of small cluster of atoms (10-15 atoms) at several places. These
cluster of atoms is called “nuclei.”
 Nucleation in metals and alloys occur by two mechanisms:
i. Homogeneous Nucleation
ii.Heterogeneous NucleationMTE/III SEMESTER/MSE/MTE 2101 58/18/2017

6.  This energy difference between the liquid and the solid is the free energy per unit volume ∆Gv and is
the driving force for solidification.
 When the solid forms, however, a solid-liquid interface is created.
 A surface free energy 𝝈sl is associated with this interface.
 Thus, the total change in energy G = -
𝟒
𝟑
πr³. ΔGv + 4πr² . σsl ….. (1)
Where
𝟒
𝟑
πr³ is volume of a spherical solid of radius r,
4πr² the surface area of a spherical solid,
ΔGv free energy change per unit volume,
σsl the surface free energy of the solid-liquid interface.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 6

7.  An embryo is a tiny particle of solid that forms from the liquid
as atoms cluster together. The embryo is unstable and may
either grow into a stable nucleus or re - dissolve.
 The top curve shows the parabolic variation of the total surface
energy 4πr² . σsl , the bottom most curve shows the total
volume free energy change
𝟒
𝟑
πr³. ΔGv .
 The curve in the middle shows the variation of ΔG. It represents
the sum of the other two curves as given by Equation 1.
 At the temperature at which the solid and liquid phases are
predicted to be in thermodynamic equilibrium (i.e., at the
freezing temperature), the free energy of the solid phase and
that of the liquid phase are equal ΔGv = 0.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 7

8.  When the solid is very small with a radius less than the critical radius
for nucleation (r*), further growth causes the total free energy to
increase.
 The critical radius (r*) is the minimum size of a crystal that must be
formed by atoms clustering together in the liquid before the solid
particle is stable and begins to grow.
 At the thermodynamic melting or freezing temperatures, the
probability of forming stable, sustainable nuclei is extremely small.
 Therefore, solidification does not begin at the thermodynamic
melting or freezing temperature.
 Because the temperature of the liquid is below the equilibrium
freezing temperature, the liquid is considered undercooled.
 The undercooling (ΔT) is the difference between the equilibrium
freezing temperature and the actual temperature of the liquid.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 8

9. HOMOGENEOUS NUCLEATION
 Homogeneous nucleation occurs when the undercooling becomes large enough to cause the
formation of a stable nucleus.
 Using the principle of maxima – minima,
differentiating equation 1 with respect to r,
𝝏(𝑮)
𝝏𝒓
= 0
We have 4πr² . ΔGv = 8πσ . r
r* = 2
𝝈
∆𝑮𝒗
It is also written as
Where ΔHf is the latent heat of fusion per unit volume, Tm is the equilibrium solidification
temperature in kelvin, and ΔT = (Tm - T) is the undercooling when the liquid temperature is T.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 9

10. Calculation of Critical Radius for the
Solidification of Copper
Q.) Calculate the size of the critical radius
the number of atoms in the critical nucleus
when solid copper forms by homogeneous
nucleation.
The lattice parameter for FCC copper is a0 =
0.3615 nm
Refer Example 9.1,”The Science and
Engineering of Materials”, Donald Askeland
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 10

11. Heterogeneous Nucleation
 Impurities in contact with the liquid, either suspended in the
liquid or on the walls of the container that holds the liquid,
provide a surface on which the solid can form.
 A radius of curvature greater than the critical radius is
with very little total surface between the solid and liquid.
 Much less undercooling is required to achieve the critical size,
so nucleation occurs more readily. Nucleation on pre - existing
surfaces is known as heterogeneous nucleation.
 This process is dependent on the contact angle (θ ) for the
nucleating phase and the surface on which nucleation occurs.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 11

12. 18/08/2017MTE/III SEMESTER/MSE/MTE 2101 12

13. Rate of Nucleation
The rate of nucleation (the number of nuclei formed per unit time) is a function of temperature.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 13

14. Planar Growth
 When a well-inoculated liquid (i.e., a liquid containing
nucleating agents) cools under equilibrium conditions,
there is no need for undercooling since heterogeneous
nucleation can occur.
 Any small protuberance that begins to grow on the
interface is surrounded by liquid above the freezing
temperature.
 The growth of the protuberance then stops until the
remainder of the interface catches up.
 This growth mechanism, known as planar growth, occurs
by the movement of a smooth solid-liquid interface into
the liquid.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 14

15. Dendritic Growth
 When the liquid is not inoculated and the nucleation is poor,
the liquid has to be undercooled before the solid forms.
 Under these conditions, a small solid protuberance called a
dendrite, which forms at the interface.
 As the solid dendrite grows, the latent heat of fusion is
conducted into the undercooled liquid, raising the
temperature of the liquid toward the freezing temperature.
 Secondary and tertiary dendrite arms can also form on the
primary stalks to speed the evolution of the latent heat.
 The container or mould must absorb the heat in planar
growth, but the undercooled liquid absorbs the heat in
dendritic growth.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 15

16. 18/08/2017MTE/III SEMESTER/MSE/MTE 2101 16

17. 18/08/2017MTE/III SEMESTER/MSE/MTE 2101 17
(a) Cooling curve for a pure metal that has not been well-inoculated. The liquid cools as specific heat is removed
(between points A and B). Undercooling is thus necessary (between points B and C). As the nucleation begins (point
C), latent heat of fusion is released causing an increase in the temperature of the liquid. This process is known as
recalescence (point C to point D). The metal continues to solidify at a constant temperature (Tmelting). At point E,
solidification is complete. The solid casting continues to cool from this point.
(b) Cooling curve for a well-inoculated, but otherwise pure, metal. No undercooling is needed. Recalescence is
not observed. Solidification begins at the melting temperature.

18. Solidification Time
 The rate at which growth of the solid occurs depends on the cooling rate, or the rate of heat extraction. The
time ts required for a simple casting to solidify completely can be calculated using Chvorinov’s rule.
where
V is the volume of the casting and represents the amount of heat that must be removed before freezing occurs,
A is the surface area of the casting in contact with the mould and represents the surface from which heat can be
transferred away from the casting,
n is a constant (usually about 2), and B is the mould constant
This rule basically accounts for the geometry of a casting and the heat transfer conditions.
The rule states that, for the same conditions, a casting with a small volume and relatively large surface area will
cool more rapidly.
18/08/2017MTE/III SEMESTER/MSE/MTE 2101 18