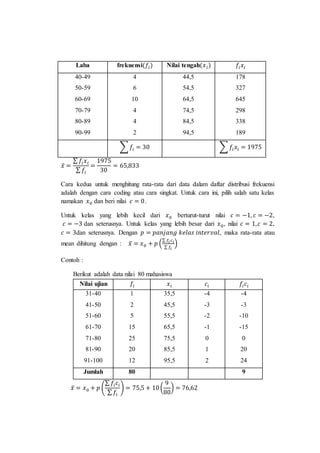
1. Dokumen ini membahas tentang tendensi sentral yang meliputi rata-rata, median, dan modus. 2. Terdapat penjelasan mengenai cara menghitung ketiga ukuran tendensi sentral tersebut baik untuk data tunggal maupun berkelompok. 3. Juga dijelaskan cara menghitung kuartil untuk membagi distribusi menjadi 4 bagian.

1. Tugas Statistika PendidikanMatematika
TENDENSI SENTRAL
Dosen pengasuh: Prof. Dr. Mukhtar, M.Pd
Oleh
DAHLIA HUDI PRATAMA
8146172011 8146172027
IMANTI AMELIA MASITAH PUSPA SARI
8146172029 8146172042
PROGRAM STUDIPENDIDIKAN MATEMATIKA KELAS B-1
PROGRAM PASCASARJANA
UNIVERSITAS NEGERI MEDAN
2014
BAB I

2. PENDAHULUAN
A. Pengertian Statistika
Sudjana (2004, dalam Riduwan dan Sunarto, 2007) mendefinisikan
statistika sebagai pengetahuan yang berhubungan dengan cara-cara pengumpulan
fakta, pengolahan serta pembuatan keputusan yang cukup beralasan berdasarkan
fakta dan analisa yang dilakukan. Sementara statistic dipakai untuk menyatakan
kumpulan fakta, umumnya berbentuk angka yang disusun dalam tabel atau
diagram yang melukiskan atau menggambarkan suatu persoalan. Lebih lanjut
Sudjana (2004, dalam Riduwan dan Sunarto, 2007) menyatakan statistika adalah
ilmu terdiri dari teori dan metode yang merupakan cabang dari matematika
terapan dan membicarakan tentang : bagaimana mengumpulkan data, bagaimana
meringkas data, mengolah dan menyajikan data, bagaimana menarik kesimpulan
dari hasil analisis, bagaimana menentukan keputusan dalam batas-batas resiko
tertentu berdasarkan strategi yang ada.
Dalam kaitannya untuk menyelesaikan masalah, pendekatan statistic
terbagi dua yaitu pendekatan statistic dalam arti sempit dan luas. Dalam arti
sempit (statistic deskriptif), yaitu kegiatan mengumpulkan data, menyusun dan
menggambarkan data dalam bentuk tabel, atau grafik serta menganalisis data yang
diperoleh tanpa menarik kesimpulan terhadap populasi secara umum. Sementara
dalam arti luas (statistic inferensi/induktif) adalah alat pengumpul data, pengolah
data, menarik kesimpulan, membuat tindakan berdasarkan analisis data yang
dikumpulkan dan hasilnya dimanfaatkan untuk populasi.
Bidang keilmuan statistika adalah sekumpulan metode untuk memperoleh
dan menganalisa data dalam pengambilan suatu kesimpulan. Meski merupakan
cabang ilmu matematika, statistika memiliki perbedaan mendasar pada logikanya.
Jika matematika menggunakan logika deduktif, sementara statistic menggunakan
logika induktif. Untuk mendapatkan gambaran yang lebih jelas tentang
sekumpulan data, selain data itu disajikan dalam tabel dan diagram masih
diperlukan ukuran-ukuran yang merupakan wakil kumpulan data tersebut antara
lain ukuran kecendrungan pusat atau tendensi sentral.

3. BAB II
PEMBAHASAN
A. Pengertian Tendensi Sentral
Tendensi Sentral adalah Ukuran pemusatan data yang ditujukan untuk
menggambarkan suatu nilai yang mewakili nilai pusat atau nilai sentral dari suatu
gugus data (himpunan pengamatan).
Ukuran Tendensi Tunggal yang mewakili data ada tiga yaitu :
1. Mean( Rata – rata )
Mean adalah rata – rata hitung suatu data. Rata-rata atau mean dilambangkan
dengan 𝑥̅.
a) Rata – rata data tunggal
Rata-rata hitung untuk data kuantitatif yang terdiri dari 𝑛 bilangan yaitu
𝑥1, 𝑥2, 𝑥3, … , 𝑥 𝑛 dihitung dengan cara membagi jumlah data oleh banyak data atau
𝑛. Secara sederhana ditulis 𝑥̅ =
∑ 𝑥 𝑛
𝑛
Contoh :
Berikut ini adalah skor tes prestasi 10 tenaga sales PT. Brawijaya :
70 56 66 94 48 82 80 70 76 50
Rata – rata skor tes tersebut adalah :
𝑥̅ =
∑ 𝑥 𝑛
𝑛
=
𝑥1+𝑥2+𝑥3 𝑥4+𝑥5+𝑥6+𝑥7+𝑥8+𝑥9+𝑥10
10
=
70+56+66+94+48+82+80+70+76+50
10
= 6,92
𝑥̅ = rata – rata
n = banyaknya data
n-= nilai data kenx

4. Jadi rata-rata skor tes prestasi 10 tenaga sales PT. Brawijaya adalah 69,2.
Jika data muncul dengan frekunsi-frekuensi maka rata-rata hitung atau mean dapat
ditentukan dengan cara berikut :
𝑥̅ =
∑ 𝑓𝑖 𝑥 𝑖
𝑛
𝑖=1
∑ 𝑓𝑖
𝑛
𝑖=1
Contoh :
Berikut ini data nilai PR lima siswa selama semester ganjil
Nilai (𝑥 𝑖) frekuensi(𝑓𝑖) 𝑥 𝑖 𝑓𝑖
70
69
45
80
56
5
6
3
1
1
350
414
135
80
56
∑ 𝑓𝑖 = 16 ∑ 𝑓𝑖 𝑥 𝑖 = 1035
𝑥̅ =
∑ 𝑓𝑖 𝑥 𝑖
𝑛
𝑖=1
∑ 𝑓𝑖
𝑛
𝑖=1
=
1035
16
= 64,6
b) Rata – rata data berkelompok
Untuk data yang telah disusun dalam daftar distribusi frekuensi dengan kelas
interval dan 𝑥 𝑖 = 𝑛𝑖𝑙𝑎𝑖 𝑡𝑒𝑛𝑔𝑎ℎ 𝑘𝑒𝑙𝑎𝑠 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙, nilai rata-rata atau mean dapat
dihitung dengan cara :
𝑥̅ =
∑ 𝑓𝑖 𝑥 𝑖
∑ 𝑓𝑖
Contoh :
Berikut ini data observasi mengenai laba setiap hari yang diperoleh
PT. Brawijaya selama 30 hari pada bulan Februari 2013

5. Laba frekuensi(𝑓𝑖) Nilai tengah(𝑥 𝑖) 𝑓𝑖 𝑥𝑖
40-49
50-59
60-69
70-79
80-89
90-99
4
6
10
4
4
2
44,5
54,5
64,5
74,5
84,5
94,5
178
327
645
298
338
189
∑ 𝑓𝑖 = 30 ∑ 𝑓𝑖 𝑥𝑖 = 1975
𝑥̅ =
∑ 𝑓𝑖 𝑥 𝑖
∑ 𝑓𝑖
=
1975
30
= 65,833
Cara kedua untuk menghitung rata-rata dari data dalam daftar distribusi frekuensi
adalah dengan cara coding atau cara singkat. Untuk cara ini, pilih salah satu kelas
namakan 𝑥0 dan beri nilai 𝑐 = 0.
Untuk kelas yang lebih kecil dari 𝑥0 berturut-turut nilai 𝑐 = −1, 𝑐 = −2,
𝑐 = −3 dan seterusnya. Untuk kelas yang lebih besar dari 𝑥0, nilai 𝑐 = 1, 𝑐 = 2,
𝑐 = 3dan seterusnya. Dengan 𝑝 = 𝑝𝑎𝑛𝑗𝑎𝑛𝑔 𝑘𝑒𝑙𝑎𝑠 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙, maka rata-rata atau
mean dihitung dengan : 𝑥̅ = 𝑥0 + 𝑝 (
∑ 𝑓𝑖 𝑐 𝑖
∑ 𝑓𝑖
)
Contoh :
Berikut adalah data nilai 80 mahasiswa
Nilai ujian 𝑓𝑖 𝑥 𝑖 𝑐𝑖 𝑓𝑖 𝑐𝑖
31-40
41-50
51-60
61-70
71-80
81-90
91-100
1
2
5
15
25
20
12
35,5
45,5
55,5
65,5
75,5
85,5
95,5
-4
-3
-2
-1
0
1
2
-4
-3
-10
-15
0
20
24
Jumlah 80 9
𝑥̅ = 𝑥0 + 𝑝 (
∑ 𝑓𝑖 𝑐𝑖
∑ 𝑓𝑖
) = 75,5 + 10(
9
80
) = 76,62

6. 2. Median
Median adalah nilai tengah dalam sekumpulan data, setelah data tersebut
disusun menurut urutan nilainya atau suatu nilai yang membatasi 50 per sen
frekuensi distribusi bagian bawah dengan 50 per sen frekuensi distribusi bagian
atas.
a) Median untuk data tunggal :
Me =
Contoh :
Berikut ini adalah skor tes prestasi 9 karyawan PT. Brawijaya :
78 56 66 94 48 82 80 70 76
Median skor tes 9 karyawan tersebut ditentukan dengan cara :
No urut 1 2 3 4 5 6 7 8 9
Nilai 48 56 66 70 76 78 80 82 94
Letak Median = 9 + 1
2
= 5
Jadi letak median pada urutan data ke 5 yaitu nilai 76
b) Median data berkelompok
𝑀𝑒 = 𝑏 + 𝑝 (
1
2⁄ 𝑛 − 𝐹
𝑓
)
Keterangan: b = batas bawah kelas median
p = panjang kelas median
n = ukuran sampel atau banyak data
F = jumlah semua frekuensi sebelum kelas median
f = frekuensi kelas median

7. Contoh : berikut ini data nilai 80 siswa
NILAI UJIAN 𝑓𝑖
31-40
41-50
51-60
61-70
71-80
81-90
91-100
1
2
5
15
25
20
12
Jumlah 80
Setengah dari seluruh data adalah 40. Jadi median akan terletak di kelas interval
kelima. Sehingga diperoleh :
𝑏 = 70,5 𝑝 = 10 𝑓 = 25
𝐹 = 1 + 2 + 5 + 15 = 23
𝑀𝑒 = 𝑏 + 𝑝 (
1
2⁄ 𝑛 − 𝐹
𝑓
)
𝑀𝑒 = 70,5 + 10 (
40 − 23
25
) = 77,3
3. Modus (Mo)
Merupakan suatu nilai yang paling sering muncul (nilai dengan frekuensi
muncul terbesar). Jika data memiliki dua modus, disebut bimodal, jika data
memiliki modus lebih dari 2, disebut multimodal.
a) Modus data tunggal
Contoh :
Berikut ini skor tes prestasi PT. Brawijaya :
70 56 66 70 48 82 80 70 76 70
Frekuensi terbesar adalah 70 yaitu ada 4 orang

8. Jadi modus skor prestasi karyawan PT. Brawijaya : 70
b) Modus data berkelompok
.𝑀𝑜 = 𝑏 + 𝑝 (
𝑏1
𝑏1+𝑏2
)
Keterangan: b = batas bawah kelas modus ialah kelas interval dengan
frekuensi terbanyak
P = panjang kelas modus
b1 = frekuensi kelas modus dikurangi frekuensi kelas interval
terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensi kelas interval
terdekat berikutnya
contoh : berikut ini data nilai 80 siswa
NILAI UJIAN Frekuensi
31-40
41-50
51-60
61-70
71-80
81-90
91-100
1
2
5
15
25
20
12
Jumlah 80
Dari soal diketahui :
b = 70,5
b1 = 25 – 15 = 10
b2 = 25 – 20 = 5
p = 80,5 – 70,5 = 10
Maka Modus dapat ditentukan dengan rumus :
𝑀𝑜 = 𝑏 + 𝑝 (
𝑏1
𝑏1+𝑏2
).

9. = 70,5 + 10 (
10
10+5
)
= 77, 17
4. Kuartil
Kuartil adalah nilai yang memisahkan tiap-tiap 25 persen dalam distribusi
frekuensi. Fungsi kuartil untuk menentukan nilai batas tiap 25 persen dalam
distribusi yang dipersoalkan. Oleh sebab itu teknik ini diterapkan jika analisis
dilakukan dengan tujuan untuk membagi distribusi menjadi 4 bagian, selanjutnya
menentukan batas tiap 25 persen distribusi dimaksud.
Dalam statistik dikenal ada 3 nilai kuartil yakni :
1. Kuartil pertama/ kuartil bawah (Q1) adalah suatu nilai yang membatasi 25%
distribusi bagian bawah dan 75 % distribusi bagian atas.
2. Kuartil kedua/kuartil tengah (Q2) adalah nilai yang membatasi 50%
distribusi bagian bawah dan 50% distribusi bagian atas. Dalam hal ini kuartil
kedua dapat diidentikkan dengan pengukuran median (Median).
3. Kuartil ketiga/ kuartil atas (Q3) adalah nilai yang membatasi 75% distribusi
bagian bawah dan 25% distribusi bagian atas.
a) Kuartil data tunggal
Letak Qi = data ke
4
)1.( ni
dengan i = 1,2, 3
Contoh
Tentukan semua kuartil pada data :
1) 4, 5, 8, 9, 7, 6, 5 (banyak data ganjil)
2) 52, 56 , 57, 60, 64, 66, 70, 75, 82, 86, 92, 94 (banyak data genap)
Jawab : 1) data diurutkan menjadi 4, 5, 5, 6, 7, 8, 9
  
Q1 Q2 Q3
Jadi kuartil bawah ( Q1 ) = 5
kuartil tengah ( Q2 ) = 6
kuartil atas ( Q3 ) = 8
2 ) 52, 56 , 57, 60, 64, 66, 70, 75, 82, 86, 92, 94
  
Q1 Q2 Q3
Letak Q1 = data ke -
(12 + 1)
4
= data ke 3
1
4

10. Letak Q2 = data ke -
2 (12 + 1)
4
= data ke 6
1
2
Letak Q3 = data ke -
3(12 + 1)
4
= data ke 9
3
4
Dengan demikian Q1 yaitu antara data ke-3 dan data ke-4 seperempat jauh
dari data ke-3. Nilai Q1 = 57 +
1
4
( data ke-4 – data ke 3 )
= 57 + ¼ ( 60 – 57 )
= 57 ¾
b) Kuartil data berkelompok
Untuk menghitung kuartil data berkelompok digunakan rumus :
Qi = kuartil ke-i
Tb = tepi bawah kelas interval Qi
P = panjang kelas interval Qi
n = f = banyak data
F = frekuensi kumulatif sebelum kelas Qi
f = frekuensi pada kelas Qi
Contoh.
Hitung nilai kuartil atas pada data berikut :
Interval F Fk
21-25
26-30
31-35
36-40
41-45
46-50
3
9
4
10
3
11
3
12
16
26
29
40
Penyelesaian :
Qi = Tb + p. 




 
f
Fni
.4
dengan i = 1,2,3 ;
untuk i = 1 (kuarti bawah);
untuk i = 2 (kuartil tengah/median);
untuk i = 3 (kuartil atas)

11. Kuartil atas (Q3) terletak pada
3(40 + 1)
4
= data ke 30
3
4
(interval 46 - 50)
Nilai Q3 = 45,5 + 5.







 
11
2940.4
3
= 45,5 +
11
5
= 45,95
5. Desil
Desil adalah suatu ukuran yang membagi sekelompok data menjadi 10
bagian sama panjang setelah data diurutkan.
Ada 9 macam desil, yaitu; desil ke-1 (D1), desil ke-2 (D2),…..,dan seterusnya
hingga desil ke-9 (D9).
a) Untuk data tunggal, jika banyak data n dan Di adalah desil ke-i, maka
Letak Di = data ke
10
)1.( ni
dengan i = 1,2,3,4,…,9
Contoh;
Tentukan D3, dan D5 dari ; 6, 4, 6, 4, 7, 5, 6, 5, 8, 7, 7, 7, 8, 6 !
Penyelesaian;
Data diurutkan menjadi ; 4, 4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8
Data 4 4 5 5 6 6 6 6 7 7 7 7 8 8
Data ke- 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Letak Di = data ke
10
)1.( ni
Letak D3 = data ke-
10
)1+14.(3
= data ke- 4 ½
Dengan interpolasi diperoleh :
Nilai D3 = x4 + 0,5(x5 – x4)
D3 = 5 + 0,5(6 – 5)
D3 = 5,5
b) Data Kelompok
Desil data berkelompok dapat dihitung dengan rumus :
Di = Tb + p. 




 
f
Fni
.10
i = 1,2,3,4,…,9

12. Dengan Di = desil ke-i
Tb = tepi bawah interval kelas Di
P = panjang kelas interval Di
n = f = banyak data
F = frekuensi kumulatif sebelum kelas Di
f = frekuensi pada kelas Di
Contoh.
Hitung nilai D5 dari data berdistribusi kelompok berikut :
Penyelesaian :
Letak Desil ke-5 =
5(40 + 1)
10
= 20 ½ (kelas interval 36-40)
Maka : D5 = 35,5 + 5 (
1
2
.40 − 16
10
)
D5 = 35,5 + 2 = 37,5
6. Persentil
Persentil adalah ukuran yang membagi sekelompok data terurut menjadi
100 bagian sama besar. Ada 99 macam persentil yang masing-masing adalah
P1, P2, P3, …, P99.
Adapun kegunaan persentil :
1. Membagi distribusi menjadi beberapa kelas yang sama besar frekuensinya
2. Menyusun norma penilaian
3. Menormalkan distribusi
Interval F Fk
21-25
26-30
31-35
36-40
41-45
46-50
3
9
4
10
3
11
3
12
16
26
29
40

13. a) Persentil data tunggal maka :
Letak Pi = data ke
100
)1.( ni
, dengan i = 1,2,3,……,99
Contoh
Tentukan P30, dan P75 dari ; 6, 4, 6, 4, 7, 5, 6, 5, 9, 7, 10, 7, 10, 6
Penyelesaian :
Data diurutkan menjadi ; 4, 4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 9, 10, 10
Data 4 4 5 5 6 6 6 6 7 7 7 9 10 10
Data ke- 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Letak Pi = data ke
100
)1+n.(i
Letak D30 = data ke-
100
)1+14.(30
= data ke- 4 ½
Dengan interpolasi diperoleh :
Nilai P3 = x4 + ½ (x5 – x4)
P3 = 5 + ½ (6 – 5)
P3 = 5,5
Letak D75 = data ke-
100
)1+14.(75
= data ke- 11 ¼
Dengan interpolasi diperoleh :
Nilai P75 = x 11 + ¼ (x 12 – x 11)
P75 = 7 + ¼ (9 – 7)
P75 = 7,5
b) Persentil data berkelompok dihitung dengan rumus :
Dengan : Pi = persentil ke-i
Tb = tepi bawah interval kelas Pi
p = panjang kelas interval Pi
n = f = banyak data
Pi = Tb + p. 




 
f
Fni
.100
i = 1,2,3,……,99

14. F = frekuensi kumulatif sebelum kelas Pi
f = frekuensi pada kelas Pi
Contoh.
Hitung nilai P 25 dari data berdistribusi kelompok berikut :
Interval f Fk
21-25
26-30
31-35
36-40
41-45
46-50
3
9
4
10
3
11
3
12
16
26
29
40
Penyelesaian ;
Letak P25 =
25(40 + 1)
100
= 10 ¼ ( kelas interval 26-30)
P25 = 25,5 + 5 (
25
100
(40) − 3
9
)
P25 = 25,5 + 3,9
= 29,4

15. BAB III
PENUTUP
A. Kegunaan Tendensial Sentral
Berdasarkan hasil pembahasan yang telah diuraikan dalam bab
sebelumnya dapat disimpulkan bahwa Tendensial Sentral memberi gambaran
umum mengenai keadaan sampel dan keadaan populasi, Meramalkan keadaan
populasi bila sampelnya representatif dan Membandingkan 2 kelompok atau lebih