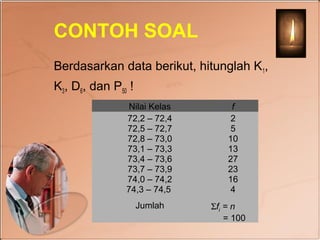
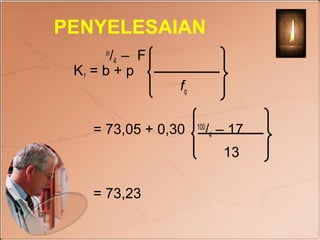
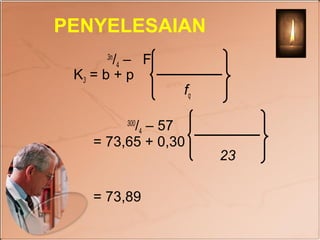
Dokumen tersebut membahas tentang statistika deskriptif kuartil, desil, dan persentil untuk mengelompokkan data. Termasuk rumus-rumus untuk menghitung nilai kuartil, desil, dan persentil baik untuk data individual maupun berkelompok beserta contoh soalnya.

1. BAB. V
STATISTIK
KUARTIL, DESIL, DAN PERSENTIL
http://zakariaib.multiply.com

2. KUARTIL
Untuk kelompok data dimana n ≥ 4, kita
tentukan tiga nilai, katakanlah K1, K2, dan K3
yang membagi kelompok data tersebut
menjadi 4 bagian yang sama, yaitu setiap
bagian memuat data yang sama atau jumlah
observasinya sama. Nilai-nilai tersebut
dinamakan nilai 25% data/observasi sama
atau lebih kecil dari K1, 50% data/observasi
sama atau lebih kecil dari K2, 75%
data/Observasi sama atau lebih kecil dari K3

3. RUMUS KUARTIL
Kalau suatu kelompok data atau nilai
sudah diurutkan dari yang terkecil (X 1)
sampai yang terbesar (Xn), maka untuk
menghitung K1, K2, dan K3 harus
dipergunakan rumus berikut :
i(n + 1)
Ki = Nilai yang ke , i = 1, 2, 3
4

4. CONTOH SOAL
Berikut ini adalah data upah dari 13
karyawan dalam ribuan rupiah, yaitu
40, 30, 50, 65, 45, 55, 70, 60, 80, 35,
85, 95, 100, (n = 13). Cari nilai K 1, K2,
dan K3.

5. PENYELESAIAN
• Pertama-tama data diurutkan dahulu :
X1=30, X2=35, X3=40, X4=45, X5=50, X6=55,
X7=60, X8=65, X9=70, X10=80, X11=85,
X12=95, X13=100.
• K1 = nilai yang ke i(n + 1)
4
= nilai ke 1(13 + 1)
4
= nilai ke-3½ (nilai yang ke 3+½(Data4-Dt3),

6. PENYELESAIAN
• Jadi :
K1 = Nilai X3+ ½(X4 - X3)
= 40 +½(45 - 40)
= 42,5
• Jadi :
K2 = nilai yang ke i(n + 1)
4
= nilai ke 2(13 + 1)
4
= nilai ke-7, nilai X7=60

7. PENYELESAIAN
Jadi :
K2 = X7 = 60
K3 = nilai ke 3(13 + 1)
4
= nilai ke-10½ (nilai yang ke-10½
berarti Data ke 10 + ½(X11- X10)

8. PENYELESAIAN
• Jadi :
K1 = X10 + ½(X11 - X10)
= 80 + ½(85 - 80)
= 82,5 (nilai kuartil tidak perlu
sesuai dengan nilai data yang
asli)

9. DESIL
Untuk kelompok data dimana n ≥ 10, dapat
ditentukan 9 nilai bagian yang sama,
misalnya D1, D2, … Q9, artinya setiap bagian
mempunyai jumlah observasi yang sama,
sedemikian rupa sehingga nilai 10%
data/observasi sama atau lebih kecil dari D1,
nilai 20% data/observasi sama atau lebih
kecil dari D2, dan seterusnya. Nilai tersebut
dinamakan desil pertama, kedua dan
seterusnya sampai desil kesembilan.

10. DESIL
Kalau suatu kelompok data atau nilai
sudah diurutkan dari yang terkecil (X 1)
sampai yang terbesar (Xn), maka
rumus desil adalah sebagai berikut :
i(n + 1)
Di = nilai yang ke , i = 1, 2, …, 9
10

11. CONTOH SOAL
Berdasarkan contoh pada kuartil
(diatas), hitunglah D1, D2, dan D9

12. PENYELESAIAN
D1 = nilai ke 1(13 + 1)
10
= nilai ke-14/10
= nilai ke-14/10, berarti X1 + 4/10(X2 – X1)
= 30 + 4/10(35 – 30)
= 32

13. PENYELESAIAN
D2 = nilai ke 2(13 + 1)
10
= nilai ke-28/10, berarti X2 + 8/10 (X3 – X2)
= 35 + 8/10 (40 – 35)
= 39
D9 = nilai ke 9(13 + 1)
10
= nilai ke-126/10, berarti X12 + 6/10 (X13 – X12)
= 95 + 6/10 (100 – 95)
= 98

14. PERSENTIL
Untuk kelompok data dimana n ≥ 100, dapat
ditentukan 99 nilai, P1, P2, … P99, yang
disebut persentil pertama, kedua dan ke-99,
yang membagi kelompok data tersebut
menjadi 100 bagian,masing-masing
mempunyai bagian dengan jumlah observasi
yang sama, dan sedemikian rupa sehingga
1% data/observasi sama atau lebih kecil dari
P1, 2% data/observasi sama atau lebih kecil
dari P2.

15. PERSENTIL
Apabila data sudah disusun mulai dari
yang terkecil (X1) sampai yang terbesar
(Xn), maka rumus persentil adalah
sebagai berikut :
i(n + 1)
Pi = nilai yang ke , i = 1, 2, …, 99
100

16. Kuartil, Desil, dan Persentil
(Data Berkelompok)
Untuk data berkelompok, yaitu data
yang sudah dibuat tabel frekuensinya,
maka rumus-rumus kuartil, desil, dan
persentil adalah sebagai berikut :
Rumus Kuartil :
in
/4 – F
Ki = b + p , i = 1,2,3
fk

17. Kuartil, Desil, dan Persentil
(Data Berkelompok)
Rumus Desil :
/10 – F
in
Di = b + p
fd
Rumus Persentil :
/100 – F
in
Pi = b + p
fp

18. KETERANGAN
Dimana :
b = nilai batas bawah dari kelas yang memuat kuartil ke-i,
desil ke-i, dan persentil ke-i
n = banyaknya observasi = jumlah semua frekuensi
F = jumlah frekuensi dari semua kelas sebelum kelas yang
mengandung kuartil ke-i, desil ke-i, dan persentil ke-i
fq = frekuensi dari kelas yang mengandung kuartil ke-i, desil
ke-i, dan persentil ke-i
p = panjangnya kelas interval yang mengandung kuartil ke-i,
desil ke-i, dan persentil ke-i
in = i kali n

19. CONTOH SOAL
Berdasarkan data berikut, hitunglah K1,
K3, D6, dan P50 !
Nilai Kelas f
72,2 – 72,4 2
72,5 – 72,7 5
72,8 – 73,0 10
73,1 – 73,3 13
73,4 – 73,6 27
73,7 – 73,9 23
74,0 – 74,2 16
74,3 – 74,5 4
Jumlah Σfi = n
= 100

20. Caranya :
Tentukan terlebih dahulu
Nilai Kelas f
letaknya msg2 Kuartil 72,2 – 72,4 2
atau Desil maupun 72,5 – 72,7 5
72,8 – 73,0 10
persentil, Misalnya : 73,1 – 73,3 13 K1
1x100
Letak K1= ∑ fi ≥
4
≥ 25 73,4 – 73,6 27
73,7 – 73,9 23 K3
74,0 – 74,2 16
3x100 74,3 – 74,5 4
Letak K3 = ∑ fi ≥
4
≥ 75
Jumlah Σfi = n
= 100

21. PENYELESAIAN
/4 – F
in
K1 = b + p
fq
= 73,05 + 0,30 100
/4 – 17
13
= 73,23

22. PENYELESAIAN
3n
/4 – F
K3 = b + p
fq
/4 – 57
300
= 73,65 + 0,30
23
= 73,89

23. PENYELESAIAN
/10 – F
6n
D6 = b + p
fd
/10 – 57
600
= 73,65 + 0,30
23
= 73,69
Artinya nilai 60% dari observasi sama
atau lebih kecil dari 73,69

24. PENYELESAIAN
/100 – F
50n
P50 = b + p
fp
/100 – 30
5000
= 73,65 + 0,30
27
= 73,57
Artinya nilai 50% dari observasi
mempunyai nilai sama atau lebih kecil
dari 73,57