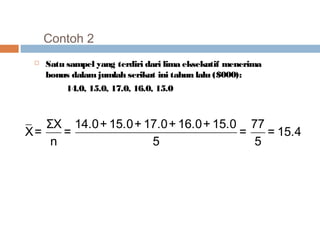
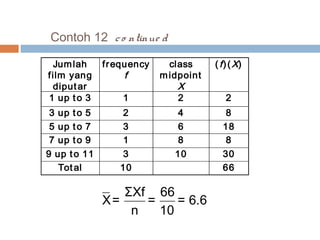
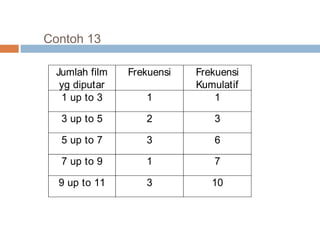
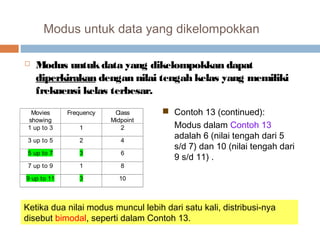
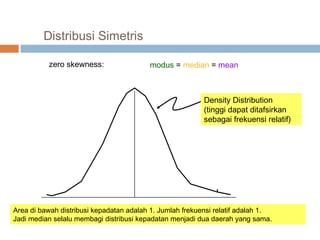
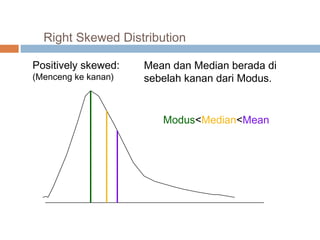
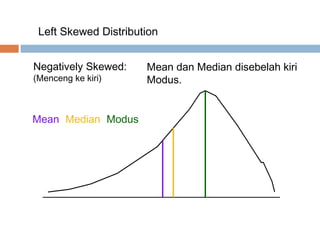
Dokumen tersebut menjelaskan berbagai ukuran nilai sentral yang digunakan untuk mendeskripsikan data, termasuk rata-rata, median, dan modus. Metode perhitungan dan karakteristik setiap ukuran nilai sentral dijelaskan untuk data yang tidak dikelompokkan dan dikelompokkan.

1. MENJELASKAN DATA
Pengukuran Nilai Sentral (Central
Tendency)

2. Pengukuran nilai sentral, meliputi
 Rata-rata Aritmatik/Hitung
 Rata-rata pembobotan
 Rata-rata Geometrik
 Rata-rata Harmonik
 Median
 Modus
 Skewness

3. Karateristik Rata-Rata
 Rata-rata Aritmetika / rata-rata hitung adalah ukuran
lokasi yang paling sering dipakai.
 Rata-rata ini dihitung dengan cara menjumlah kan semua
nilai dan membaginya dengan banyaknya nilai tersebut.
 Karakteristik utama rata-rata adalah:
 Memerlukan data dalam skala intervaI atau rasio.
 Semua nilai dipakai.
 Unik (dalam satu kelompok data hanya ada satu
rata-rata).
 Jumlah semua deviasi dari rata-rata adalah 0.

4. Population Mean
 Untuk yang tidak dikelompokkan, rata-rata populasi adalah
jumlah dari semua nilai populasi dibagi dengan jumlah total nilai
populasi:
X
μ = Σ
N
dimana μ adalah rata-rata populasi.
N adalah jumlah total observasi.
X adalah nilai tertentu.
S menunjukkan operasi penjumlahan.

5. Contoh 1
 Contoh 1: Keluarga Budi memiliki 4 mobil. Berikut
ini adalah jarak yang sudah ditempuh masing-masing
mobil:
56,000, 23,000, 42,000, 73,000
Hitung rata-rata jarak yang sudah ditempuh keempat
mobil.
56,000+ ...+ 73,000
4 = 48,500
X
μ = Σ
N =

6. Sample Mean
 Untuk data yang tidak dikelompokkan, rata-rata sampel
adalah jumlah semua nilai sampel dibagi jumlah sampel:
ΣX
n
X=
dimana n adalah jumlah total sampel.
Rata-rata sampel juga disebut rata-rata aritmetik atau
rata-rata sampel.

7. Contoh 2
 Satu sampel yang terdiri dari lima eksekutif menerima
bonus dalam jumlah serikut ini tahun lalu ($000):
14.0, 15.0, 17.0, 16.0, 15.0
ΣX 14.0+ 15.0+ X= = 17.0+ 16.0+ 15.0 = 77 = 15.4
n 5 5

8. Contoh 2 (continued)
 Satu sampel yang terdiri dari lima eksekutif menerima
bonus dalam jumlah serikut ini tahun lalu ($000):
7.0, 15.0, 17.0, 16.0, 15.0
 Merubah observasi pertama dari 14.0 menjadi 7.0 akan
merubah rata-rata sampel.
= 77
= 15.4
5
= 14.0+ ...+ 15.0
n
5
X= ΣX
= 70
= 14
5
= 7.0+ ...+ 15.0
n
5
X= ΣX

9. Contoh 3
 Misalnya ada satu set nilai: 3, 8, dan 4. Rata-ratanya
adalah 5. Perhitungan berikut menunjukkan
properti kelima dari rata-rata :
x (x- x bar)
3 (3-5)= -2
8 (8-5)= 3
4 (4-5)= -1
Σ= 15 Σ= 0

10. Weighted Mean (Rata-rata Pembobotan)
 Rata-rata pembobotan dari satu set angka X1, X2, ..., Xn,
dengan bobot masing-masing w1, w2, ...,wn, dihitung
dengan rumus sebagai berikut:
(w X + w X + ...+ w X )
1 1 2 2 n n
w (w + w + ...w
1 2 n )
X =
Bobot (w)  Jumlah frekuensi

11. Contoh 4
 Dalam satu jam, seorang penjual minuman ringan
berhasil menjual 50 minuman. Dia menjual lima
minuman seharga $0.50, lima belas seharga $0.75, lima
belas seharga $0.90, dan lima belas seharga $1.15.
Hitung rata-rata tertimbang harga minuman yang
terjual.
X = $44.50 = $0.89
w
50
w x (w . x)
5 0.50 2.50
15 0.75 11.25
15 0.90 13.50
15 1.15 17.25
Σ= 50 Σ= 44.50

12. Geometric Mean
 Geometric mean (GM) atau Rata-rata geometrik dari
satu set angka n adalah akar pangkat n dari perkalian
angka n . Formulanya adalah sbb:
G n X X X Xn
( 1)( 2)( 3)...( )
log
n
X
=
G
å =
log
Rata-rata geometrik dipergunakan untuk menghitung
rata-rata persentase, indeks, atau angka relatif.
 Rata-rata geometrik tidak dapat dihitung bila ada
angka yang negatif.

13. Contoh 7
 Tingkat suku bunga pada 3 surat obligasi 5, 21, dan 4
persen.
 Rata-rata geometric :
GM= 3 (5)(21)(4) = 7.49
 Rata-rata arithmetic: (5+21+4)/3 =10.0
 GM menghasilkan angka profit yang lebih konservatif
karena tidak terlalu dipengaruhi oleh suku bunga
terbesar, 21 %.

14. Geometric Mean c o ntinue d
 Penggunaan lain dari rata-rata geometrik adalah
untuk menghitung persentase kenaikan penjualan,
produksi atau aktivitas bisnis atau ekonomi dari satu
periode ke periode yang lain:
GM= (Nilai akhir periode) n -
1
(Nilai awal periode)

15. Contoh 8
 Jumlah total perempuan yang terdaftar pada
Universitas di Amerika meningkat dari 755,000 pada
tahun 1992 menjadi 835,000 pada tahun 2000. Berapa
rata-rata geometrik tingkat pertumbuhannya?
835,000
755,000 - 1 = .0127
GM= 8

16. Contoh 9
 Seorang investor ingin memperoleh hasil 100% dalam
waktu satu tahun dari investasi pada bisnisnya. Berapa
persentase hasil (return) yang harus diperoleh setiap
bulan?
- 1 = .059
GM= 12 200
100
Bisnisnya harus menghasilkan return 5.9% setiap bulan.

17. Contoh 10
 Pemerintah Cina pada tahun 1990 menyatakan bahwa
PDB mereka akan meningkat dua kali lipat dalam 20
tahun. Berapa tingkat pertumbuhan tahunan PDB agar
impian ini menjadi kenyataan?
- 1 = .035
GM= 20 200
100
Pertumbuhan tahunan PDB 3.5%.

18. Harmonic Mean
 Rumus :
H n1
å
=
i X
 Contoh :
Pimpinan perusahaan memberikan dana masing-masing
Rp 100 juta kepada tiga dep (A,B,C) untuk
pemb komp. Dep A melaporkan harga per unit
komputer Rp 5 juta, dep B melaporkan Rp 4 juta dan
dep C melaporkan Rp 4,5 juta. Berapa rata-rata harga
komputer tersebut ?
4.462.809,92
4,5
1
4
1
5
1
3 =
+ +
H =

19. The Median
 Median adalah nilai tengah dari satu set nilai yang
telah diurutkan dari nilai terkecil sampai nilai terbesar.
 Letak median= n+1
2
 Untuk satu set data yang ganjil, median akan tepat
berada di tengah.
 Untuk satu set data yang genap, median dihitung
dengan rata-rata hitung dari dua nilai tengah.

20. Contoh 5
 Data umum dari satu sampel yang terdiri dari 5
mahasiswa adalah sbb:
21, 25, 19, 20, 22
 Susun data tsb dari kecil ke besar:
19, 20, 21, 22, 25. Sehingga median adalah 21.
Tinggi badan empat pemain basket (dlm inci), adalah sbb:
76, 73, 80, 75
Susun data tersebut dari kecil ke besar, sehingga
menjadi:
73, 75, 76, 80. Median: (75+76)/2= 75.5

21. Karakteristik Median
1. Dalam satu data set ada satu median (unik).
2. Median tidak dipengaruhi oleh nilai yang terlalu
besar maupun terlalu kecil. Oleh karena itu,
median menjadi ukuran sentral yang penting
ketika ada nilai yang semacam itu.
3. Dapat dihitung pada data skala rasio, interval,
maupun ordinal.

22. The Mode (Modus)
 Modus adalah nilai observasi yang peling sering
muncul.
 Dalam satu data set, dimungkinkan ada lebih dari satu
modus.
 Contoh 6: Nilai ujian sepuluh orang siswa adalah sbb:
81, 93, 84, 75, 68, 87, 81, 75, 81, 87.
Karena nilai 81 paling sering muncul, maka nilai
tersebut adalah Modus.

23. MEAN, MEDIAN &
MODUS
untuk data yang dikelompokkan
(Distribusi Frekuensi)

24. Rata-rata untuk Data yang dikelompokkan
 Mean (rata-rata) dari data sampel yang disusun dalam
distribusi frekuensi dihitung dengan rumus berikut:
x = Σxf
n
di mana:
• x : nilai tengah kelas
• f : frekuensi kelas
• n : jumlah observasi

25. Contoh 12
 Sebuah sampel yang
terdiri dari sepuluh
bioskop di Surabaya
dihitung jumlah film
yang diputar minggu
lalu. Hitunglah jumlah
rata-rata film yang
diputar.
Jumlah
film yang
diputar
frequency
f
1 up to 3 1
3 up to 5 2
5 up to 7 3
7 up to 9 1
9 up to 11 3
Total 10

26. Contoh 12 c o ntinue d
= 66
n
= 6.6
10
X= ΣXf
Jumlah
film yang
diputar
frequency
f
class
midpoint
X
(f ) (X)
1 up to 3 1 2 2
3 up to 5 2 4 8
5 up to 7 3 6 18
7 up to 9 1 8 8
9 up to 11 3 10 30
Tot al 10 66

27. Median untuk Data yang dikelompokkan
 Median suatu data sampel yang disusun dalam
distribusi frekuensi dihitung dengan cara berikut:
2 CF
f (i)
n
Median= L+
-
di mana:
• L adalah batas bawah kelas median
• CF adalah frekuensi kumulatif sebelum kelas median,
• f adalah frekuensi kelas median
• i adalah interval kelas median.

28. Menentukan kelas Median
 Untuk menentukan kelas median untuk data kelompok:
 Buatlah distribusi frekuensi kumulatif.
 Lalu bagi jumlah total data dengan 2.
 Tentukan kelas akan berisi nilai ini. Untuk Contoh,
jika n = 50, 50 / 2 = 25, kemudian tentukan kelas
akan berisi nilai urutan ke 25.

29. Contoh 13
Jumlah film
yg diputar
Frekuensi Frekuensi
Kumulatif
1 up to 3 1 1
3 up to 5 2 3
5 up to 7 3 6
7 up to 9 1 7
9 up to 11 3 10

30. Contoh 13 c o ntinue d
 Dari tabel kita peroleh:
L=5, n=10, f=3, i=2, CF=3
10
2 3
3 (2) = 6.33
2 CF
f (i) = 5+
n
Median= L+
- -

31. Modus untuk data yang dikelompokkan
 Modus untuk data yang dikelompokkan dapat
diperkirakan dengan nilai tengah kelas yang memiliki
frekuensi kelas terbesar.
Movies
showing
Frequency Class
Midpoint
1 up to 3 1 2
3 up to 5 2 4
5 up to 7 3 6
7 up to 9 1 8
9 up to 11 3 10
 Contoh 13 (continued):
Modus dalam Contoh 13
adalah 6 (nilai tengah dari 5
s/d 7) dan 10 (nilai tengah dari
9 s/d 11) .
Ketika dua nilai modus muncul lebih dari satu kali, distribusi-nya
disebut bimodal, seperti dalam Contoh 13.

32. Modus untuk data kelompok
 Modus untuk data yang dikelompokkan dapat
dihitung dengan formula berikut:
 Formula :
æ ö
M L d i
= +ç ¸ è + ø
æ ö
= -ç ¸ è + ø
 d1: f kelas modus - f kelas sebelum kelas modus
 d2: f kelas modus – f kelas sesudah kelas modus
1
0
1 2
2
1 2
o
d d
M U d i
d d

33. Movies
showing
Frequency Class
Midpoint
1 up to 3 1 2
3 up to 5 2 4
5 up to 7 3 6
7 up to 9 1 8
9 up to 11 3 10
æ ö æ - ö = + ç ¸ = + ç ¸´ = + = è + ø è - + - ø
1 3 2 2 1
5 2 5 5.67
0
1 2
æ ö æ - ö = + ç 1
= + = + = è + ¸ ç ø è - + - ¸´ ø
0
1 2
(3 2) (3 1) 3
2 9 3 1 2 9 4 9.8
(3 1) (3 0) 5
M L d i
d d
M L d i
d d

34. EXAMPLE
Penjualan f X
20-<30 4 25
30-<40 7 35
40-<50 8 45
50-<60 12 55
60-<70 9 65
70-<80 8 75
80-<90 2 85
50
æ
= + - o M
50 (12 8) = ÷ ÷ø
10 55,7
(12 8) (12 9)
ö
ç çè
- + -

35. Distribusi Simetris
zero skewness: modus = median = mean
Density Distribution
(tinggi dapat ditafsirkan
sebagai frekuensi relatif)
Area di bawah distribusi kepadatan adalah 1. Jumlah frekuensi relatif adalah 1.
Jadi median selalu membagi distribusi kepadatan menjadi dua daerah yang sama.

36. Right Skewed Distribution
Positively skewed:
(Menceng ke kanan)
Mean dan Median berada di
sebelah kanan dari Modus.
Modus<Median<Mean

37. Left Skewed Distribution
Negatively Skewed:
(Menceng ke kiri)
Mean dan Median disebelah kiri
Modus.
Mean<Median<Modus

38. Latihan soal no. 58
f X f.x fk
0 -< 5 2 2.5 5 2
5 -< 10 7 7.5 52.5 9
10 -< 15 12 12.5 150 21
15 -< 20 6 17.5 105 27
20 -< 25 3 22.5 67.5 30
30 380
x = Σf ´x = =
a. Mean 380 12.67
30
n
b. Kelas Median 30/2=15  Kelas: 10-<15
n CF 30
- - 9
Median= L+ 2 (i) = 10+ 2 (5) = 12.5
12 m
f
c. Kelas Modus 10-<15
æ ö æ - ö = + ç 1
¸ = + + ç ¸´ = è ø è - + - ø
0
1 2
10 12 7 5 10.83
(12 7) (12 6)
M L d i
d d

39. Latihan soal no. 59
f X f.x fk
20 -< 30 7 25 175 7
30 -< 40 12 35 420 19
40 -< 50 21 45 945 40
50 -< 60 18 55 990 58
60 -< 70 12 65 780 70
70 3310
x = Σf ´x = =
a. Mean 3310 47.28
70
n
b. Kelas Median 70/2=35  Kelas: 40-< 50
n CF 70
- -19
Median= L+ 2 (i) = 40+ 2 (10) = 40+ 7.62= 47.62
21 m
f
c. Kelas Modus 40-<50
æ ö æ - ö = + ç 1
¸ = + + ç ¸´ = è ø è - + - ø
0
1 2
40 21 12 10 47.5
(21 12) (21 18)
M L d i
d d

40. Latihan soal no. 60
f X f.x fk
10-<20 3 15 45 3
20-<30 7 25 175 10
30-<40 18 35 630 28
40-<50 20 45 900 48
50-<60 12 55 660 60
60 175 2410
x = Σf ´x = =
a. Mean 2410 40.17
60
n
b. Kelas Median 60/2=30  Kelas: 40-< 50
n CF 60
- - 28
Median= L+ 2 (i) = 40+ 2 (10) = 40+ 1= 41
20 m
f
c. Kelas Modus 40-<50
æ ö æ - ö = + ç 1
¸ = + + ç ¸´ = è ø è - + - ø
0
1 2
40 20 18 10 41
(20 18) (20 12)
M L d i
d d