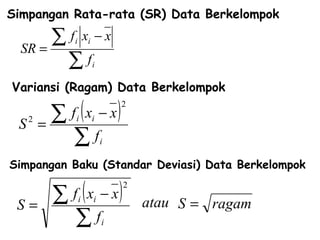
Dokumen ini menjelaskan metode perhitungan statistik data berkelompok, termasuk rataan hitung, median, dan modus, serta cara menghitung kuartil, desil, dan persentil. Terdapat contoh perhitungan yang menunjukkan penggunaan rumus-rumus untuk menentukan nilai statistik tersebut dari tabel distribusi frekuensi. Selain itu, juga dibahas mengenai simpangan rata-rata, variansi, dan simpangan baku pada data berkelompok.

1. STATISTIK DATA BERKELOMPOK
Mean (Rataan Hitung)
(ii). Metode Titik Tengah
∑fx
X=
∑f
i i
i
(ii). Metode Rataan Sementara
X = Xs
∑fd
+
∑f
i
i
i
(iii). Metode Pengkodean(Coding)
Xs = nilai rata-rata hitung sementara
di = Xi – Xs
Xi = titik tengah kelas
c = panjang kelas
 ∑ f iU i 
c
X = Xs +
 ∑f 
i 

xi − xs
Ui =
c

2. tb = Tepi bawah kelas median
Median
 n−∑
M e = tb + 

f0

1
2
f 
c


c = panjang kelas
∑f = jumlah frekuensi sebelum median
f0 = frekuensi median
n = jumlah semua frekuensi
Modus
Modus untuk data berkelompok ditentukan dengan rumus :
 d1 
M 0 = tb + 
 d + d C

2 
 1
tb = tepi bawah kelas
c = panjang kelas
fo = frekuensi kelas modus
d1 = f0 – f -1
d2 = f0 – f+1
f+1 = frekuensi kelas sesudah kelas modus
f-1 = frekuensi kelas sebelum kelas modus

3. Contoh :
Perhatikan Tabel Distribusi
frekuensi disamping
Tentukanlah :
a. Rataan Hitung (Mean)
b. Median
c. Modus
Jawab : Cara 1 :
Interval
fi
xi
fixi
22 – 26
27 – 31
32 – 36
37 – 41
5
12
9
4
24
29
34
39
120
348
306
156
30
930
Interval
Frekuensi
22 – 26
27 – 31
32 – 36
37 – 41
5
12
9
4
∑fx
X=
∑f
i i
i
930
=
30
= 31

4. Jawab :
Cara 2 :
Interval
fi
xi
di = x i – xs
fidi
22 – 26
27 – 31
32 – 36
37 – 41
5
12
9
4
24
29
34
39
-5
0
5
10
-25
0
45
40
30
X s = 29
X = Xs
∑fd
+
∑f
i
i
60
= 29 +
30
= 29 + 2
60
= 31
Cara 3 :
Interval
fi
xi
ui
fiui
22 – 26
27 – 31
32 – 36
37 – 41
5
12
9
4
24
29
34
39
-1
0
1
2
-5
0
9
8
30
12
X s = 29
Ui =
xi − xs
c
 ∑ f iU i 
c
X = Xs +
 ∑f 
i 

12
.5
30
= 29 + 2
= 31
= 29 +
i

5. Jawab : Median
Interval
fi
∑fk
22 – 26
27 – 31
32 – 36
37 – 41
5
12
9
4
5
17
26
30
 1 n−∑
M e = tb +  2

f0

 10 
= 26,5 +  5
 12 
= 26,5 + 4,17
= 30,67
Modus
Interval
fi
22 – 26
27 – 31
32 – 36
37 – 41
5
12
9
4
d1 = 12 – 5 = 7
d2 = 12 – 9 = 3
f 
 1 (30) − 5 
c = 26,5 +  2
5

 12


 d1 
M 0 = tb + 
 d + d C

2 
 1
 7 
= 26,5 + 
5
 7 +3
= 26,5 + 3,5
= 30

6. Kuartil
Kuartil untuk data berkelompok dapat ditentukan dengan
menggunakan rumus :tb = Tepi bawah kelas kuartil ke i (1,2,3)
i
 4 n − ∑ f k  c = panjang kelas
c
Qi = tb + 

 ∑f = jumlah frekuensi sebelum kuartil ke-i
f0


f0 = frekuensi kuartil ke-i
Desil
i
 10 n − ∑ f k 
c
Di = tb + 


f0


Persentil
i
 100 n − ∑ f k 
c
Pi = tb + 


f0


n = jumlah semua frekuensi
tb = Tepi bawah kelas desil ke-i
(1,2,3....9)
tb = Tepi bawah kelas persentil ke-i
(1,2,3....99)

7. Contoh :
Interval
b. Jangkauan Antar Kuartil
c. Simpangan Kuartil
Jawab :
Interval
fi
∑fk
1–5
6 – 10
11 – 15
16 – 20
21 – 25
26 – 30
3
5
10
15
4
3
3
8
18
33
37
40
Letak Q1 pada frekuensi
= ¼(40)= 10 di kelas 11 – 15
Frekuensi
1–5
6 – 10
11 – 15
16 – 20
21 – 25
26 – 30
Perhatikan Tabel Distribusi
frekuensi disamping
Tentukanlah :
a. Q1, Q2 dan Q3
3
5
10
15
4
3
 1 n − ∑ fk 
c
Q1 = tb +  4


f0


 1 (40) − 8 
= 10,5 +  4
5
 10

2
= 10,5 +  
2
= 10,5 + 1
= 11,5

8. Interval
fi
∑fk
1–5
6 – 10
11 – 15
16 – 20
21 – 25
26 – 30
3
5
10
15
4
3
3
8
18
33
37
40
Letak Q2 pada frekuensi
= ½ (40)= 20 di kelas 16 – 20
Interval
fi
∑fk
1–5
6 – 10
11 – 15
16 – 20
21 – 25
26 – 30
3
5
10
15
4
3
3
8
18
33
37
40
Letak Q3 pada frekuensi
= ¾(40)= 30 di kelas 16 – 20
 1 n − ∑ fk 
c
Q2 = tb +  2


f0


 1 (40) − 18 
= 15,5 +  2
5
15


2
= 15,5 +  
3
= 15,5 + 0,67
= 16,17
 3 n − ∑ fk 
c
Q3 = tb +  4


f0


 3 (40) − 18 
= 15,5 +  4
5
15


 12 
= 15,5 +  
3
= 15,5 + 4
= 19,5

9. b Jangkauan Antar Kuartil = Q3 – Q1
= 19,5 – 11,5
=8
c. Jangkauan Antar Kuartil = ½(Q3 – Q1)
= ½(19,5 – 11,5)
= ½ (8)
=4
Contoh :
Perhatikan Tabel Distribusi
frekuensi disamping
Tentukanlah :
a. Desil ke-3
b. Persentil ke 85
Interval
Frekuensi
4–7
8 – 11
12 – 15
16 – 19
20 – 23
24 – 27
8
10
16
40
16
10

10. Jawab :
Interval
fi
∑fk
4–7
8 – 11
12 – 15
16 – 19
20 – 23
24 – 27
8
10
16
40
16
10
8
18
34
74
90
100
Letak Q2 pada frekuensi
3
= 10 (100)= 30 di kelas 12 – 15
Interval
fi
∑fk
4–7
8 – 11
12 – 15
16 – 19
20 – 23
24 – 27
8
10
16
40
16
10
8
18
34
74
90
100
Letak Q2 pada frekuensi
85
= 100 (100)= 85 di kelas 20 – 23
3
 10 n − ∑ f k 
c
D3 = tb + 


f0


3
 10 (100) − 18 
= 11,5 + 
4
16


 12 
= 11,5 +  
4
= 11,5 + 3
= 14,5
85
 100 n − ∑ f k 
c
P85 = tb + 


f0


85
 100 (100) − 74 
= 19,5 + 
4
16


 11 
= 19,5 +  
4
= 19,5 + 2,75
= 22,25

11. Simpangan Rata-rata (SR) Data Berkelompok
∑ f x −x
SR =
∑f
i
i
i
Variansi (Ragam) Data Berkelompok
S
2
∑ f ( x − x)
=
∑f
i
2
i
i
Simpangan Baku (Standar Deviasi) Data Berkelompok
S=
∑ f ( x − x)
∑f
i
i
i
2
atau S = ragam

12. Contoh :
Interval
Perhatikan Tabel Distribusi
frekuensi disampingTentukanlah 22 – 26
27 – 31
:
32 – 36
a. Simpangan Rata-rata
37 – 41
b. Ragam (variansi)
c. Simpangan Baku
Jawab : a. Simpangan rata-rata
Interval
fi
xi
fixi
|xi – x|
fi |xi – x|
22 – 26
27 – 31
32 – 36
37 – 41
5
12
9
4
24
29
34
39
120
348
306
156
7
2
3
8
35
24
27
32
30
930
108
Frekuensi
5
12
9
4
∑fx
X=
∑f
i i
=
i
930
= 31
30
∑ f x −x
SR =
∑f
i
i
i
108
=
30
= 3,6

13. Jawab : b. ragam (variansi)
Interval
fi
xi
f ix i
(xi – x)
(xi – x)
22 – 26
27 – 31
32 – 36
37 – 41
5
12
9
4
24
29
34
39
120
348
306
156
-7
-2
3
8
49
4
9
64
30
2
fi (xi – x)
2
2
2
22 – 26
27 – 31
32 – 36
37 – 41
fi
5
12
9
4
30
xi
24
29
34
39
fixi
120
348
306
156
930
(xi – x)
-7
-2
3
8
(xi – x)
49
4
9
64
fi (xi – x)
245
48
81
256
630
i
630
=
30
= 21
c. Simpangan Baku (standar deviasi)
Interval
i
i
630
2
i i
i
245
48
81
256
930
∑ f x = 930 = 31
X=
30
∑f
∑ f ( x − x)
S =
∑f
2
∑ f x = 930 = 31
X=
30
∑f
∑ f ( x − x)
S=
∑f
i i
i
2
i
i
i
630
=
= 21
30

14. 37. Persentil ke-75 dari data: 8, 6, 4, 3, 2, 9, 10, 15, 12, 14
adalah ….
a. 11
b. 11,5
c. 12,5
d. 12,75
e. 13
38. Simpangan rataan hitung data 10, 10, 9,8, 8, 7, 7, 6, 6, 5
adalah ....
a. 7,6
b. 6,6
c. 2,8
d. 2,2
e. 1,4

15. 39. Simpangan baku dari tabel di bawah ini adalah ….
Interval
Frekuensi
a. 6 3
b. 7 2
41 – 50
1
51 – 60
7
c. 4 6
61 – 70
10
d. 91
71 – 80
6
e. 86
81 – 90
2
40.
Nilai
4
5
6
8
10
Frekuensi 20
40
70
a
10
Dalam tabel di atas, nilai rataan hitung ujian matematika
adalah 6. Oleh karena itu, a adalah ....
a.0
b.5
c.10
d.20
e. 30

16. Persentil (data tunggal)
Jika data dibagi menjadi 100 bagian yang sama, maka ukuran
itu disebut persentil. Letak persentil dirumuskan dengan:
Keterangan: Pi = persentil ke-i
i = 1, 2, 3, . . ., 99
n = banyaknya data
Contoh :
Diketahui: 9, 10, 11, 6, 8, 7, 7, 5, 4, 5, tentukan persentil ke-30
dan persentil ke-75.
Jawab :
Data diurutkan: 4, 5, 5, 6, 7, 7, 8, 9, 10, 11

17. Jawab :