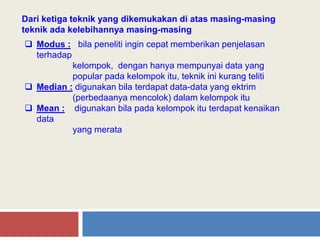
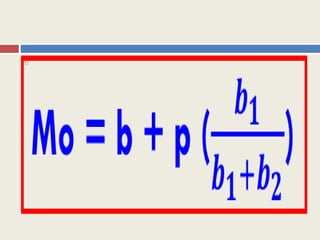
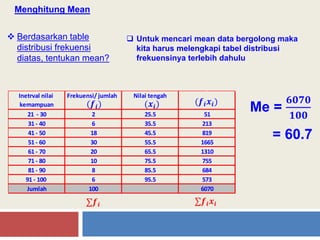
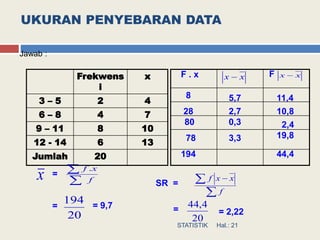
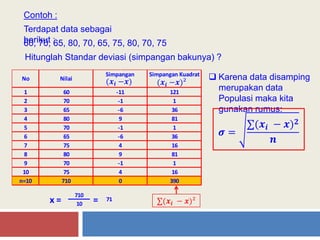
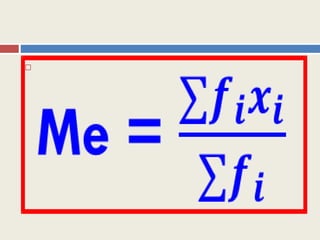Dokumen ini menjelaskan tentang statistik deskriptif dengan fokus pada pengukuran gejala pusat yaitu modus, median, dan mean. Modus adalah nilai yang paling sering muncul, median adalah nilai tengah dari data yang terurut, dan mean adalah nilai rata-rata. Selain itu, juga dibahas tentang ukuran penyebaran data seperti jangkauan, simpangan rata-rata, varians, dan standar deviasi.

1. Statistik Deskriptif
Pengukuran Gejala Pusat (central Tendency
Modus, median dan mean merupakan teknik statistic yang digunakan
untuk menjelaskan kelompok yang berdasarkan atas gejala pusat
(tendency central) dari kelompok tersebut.
Modus
(Mode)Modus adalah : teknik penjelasan kelompok yang didasarkan atas nilai
yang sedang popular (yang sedang menjadi mode) atau yang sering
muncul dalam kelompok tersebut.
Contoh Modus
Untuk data Kuantitatif
1. Seorang peneliti datang ke Yogyakarta, dan melihat para siswa dan
mahasiswa banyak yang naik sepeda motor. Selanjutnya peneliti dapat
menjelaskan dengan modus, bahwa (kelompok) siswa dan mahasiswa di
Yogyakarta banyak yang naik sepeda motor
2. Kebanyakan pemuda Indonesia menghisap Rokok
3. Pada umumnya pegawai negeri tidak disiplin kerja

2. Untuk data Kualitatif
 Dari hasil observasi(pengamatan) terhadap pegawai di
Departemen Kesehatan, nilai kinerja yang diperoleh
adalah:
20, 45, 60, 56, 45, 45, 20, 19, 57, 45, 45, 51, 35Dari data Modusnya adalah 45
 Modus bisa lebih dari satu, misal ada data :
20, 21, 25, 25, 24, 27, 27, 28, 29, 29, ,30
Maka Modusnya : 25, 27, dan
29

3. Median
Median adalah salah satu teknik penjelasan kelompok yang
didasarkan atas nilai tengah dari kelompok data yang telah disusun
berdasarkan urutannya dari yang terkecil sampai yang terbesar atau
sebaliknyaContoh:
 Data yang telah diurutkan (jumlah data
Ganjil)
19 20 20 35 45 45 45 45 45 51 56 57 60
Medianya 45
 Data yang telah diurutkan (jumlah data
Genap)
180 171 170 167 166 165 164 160 147 145
Mediannya :
2
166 + 165
= 165.5

4. Mean
Mean Merupakan teknik Penjelasan kelompok yang didasarkan atas
nilai rata-rata dari kelompok tersebut
𝑀𝑒 =
∑𝑥𝑖
𝑛
Me = Mean (rata-rata)
∑ = Epsilon (bacaJumlah)
𝑥𝑖= Nilai x ke I sampai n
n = jumlahIndividu
Contoh :
sepuluh pegawai di PT Samudra penghasilah perminggunya
adalh sebagai berikut (dalam satuan Ribu rupiah)
90, 120, 160, 60 , 180, 190, 90, 180, 70, 160
1300
1010
=
= 130
Me =
90 + 120 + 160 + 60 + 180 + 190 + 90 + 180 + 70 + 160

5.  Modus : bila peneliti ingin cepat memberikan penjelasan
terhadap
kelompok, dengan hanya mempunyai data yang
popular pada kelompok itu, teknik ini kurang teliti
 Median : digunakan bila terdapat data-data yang ektrim
(perbedaanya mencolok) dalam kelompok itu
 Mean : digunakan bila pada kelompok itu terdapat kenaikan
data
yang merata
Dari ketiga teknik yang dikemukakan di atas masing-masing
teknik ada kelebihannya masing-masing

6. Menghitung mean
Berikut adalah data tentang kinerja bidan di
kabupaten Bangkalan
61 - 70 20
Inetrval nilai
kemampuan
Frekuensi/ jumlah
21 - 30 2
31 - 40 6
Jumlah 100
71 - 80 10
81 - 90 8
91 - 100 6
41 - 50 18
51 - 60 30

7. 

8. 

9. Menghitung
 Berdasarkan table
distribusi frekuensi
diatas, tentukan
modusnya?
b = 51 – 0.5 = 50.5 atau 𝟓𝟎+𝟓𝟏
𝟐
= 50.5
𝐛 𝟏 = 30 – 18 = 12
𝐛 𝟐 = 30 – 20 = 10
Mo = 50.5 + 10 (
𝟏𝟐
𝟏𝟐+𝟏𝟎
)
p = 60.5 – 50.5.5 = 10
= 50.5 + 10 (0.545)
= 50.5 + 5.45
= 55.95
61- 70 20
Inetrval nilai
kemampuan
Frekuensi/jumlah
21 - 30 2
31- 40 6
Jumlah 100
71- 80 10
81- 90 8
91- 100 6
41- 50 18
51- 60 30

10. 

11. 

12. 61- 70 20
Inetrval nilai
kemampuan
Frekuensi/jumlah
21 - 30 2
31- 40 6
Jumlah 100
71- 80 10
81- 90 8
91- 100 6
41- 50 18
51- 60 30
Menghitung
Median
 Berdasarkan table
distribusi frekuensi
diatas, tentukan
mediannya?
Dalam hal ini kelas median dapat dicari dengan
cara :
2 + 6 + 18 = 26
𝟓𝟎+𝟓𝟏
𝟐
= 50.5
𝒇 =
𝐅 =
Md = 50.5 + 10 (
𝟓𝟎 −𝟐𝟔
𝟑𝟎
)
b =
60.5 – 50.5.5 = 10
= 50.5 + 10 (0.8)
= 50.5 + 8
= 58.5
setengah x total frekuensi=
𝟏
𝟐
𝒙 𝐧 =
𝟏
𝟐
𝒙 𝟏𝟎𝟎 =
𝟓𝟎
56
51 – 0.5 = 5.5 atau
p =
30

13. 

14. 

15. Menghitung Mean
 Berdasarkan table
distribusi frekuensi
diatas, tentukan mean?
 Untuk mencari mean data bergolong maka
kita harus melengkapi tabel distribusi
frekuensinya terlebih dahulu
1310
755
684
573
6070
51
213
819
1665
65.5
75.5
85.5
95.5
Nilai tengah
25.5
35.5
45.5
55.5
61 - 70 20
Inetrval nilai
kemampuan
Frekuensi/ jumlah
𝑓
21 - 30 2
31 - 40 6
Jumlah 100
71 - 80 10
81 - 90 8
91 - 100 6
41 - 50 18
51 - 60 30
(𝒇𝒊) (𝒙𝒊) (𝒇𝒊 𝒙𝒊)
∑𝒇𝒊 𝒙𝒊∑𝒇𝒊
Me =
𝟔𝟎𝟕𝟎
𝟏𝟎𝟎
= 60.7

16. Ukuran penyebaran data adalah
suatu ukuran yang menyatakan seberapa besar nilai-nilai data berbeda
atau bervariasi dengan nilai ukuran pusatnya atau seberapa besar
penyimpangan nilai-nilai data dengan nilai pusatnya.
Hal.: 16STATISTIK
Jangkauan adalah selisih antara nilai maksimum dan nilai minimum
yang terdapat dalam data.
Jangkauan dapat dihitung dengan rumus:
R = X maks – X min
Contoh :
Tentukan range dari data : 10,6,8,2,4
Jawab :
R = Xmaks – Xmin = 10 – 2 = 8
1. Jangkauan ( Range )
UKURAN PENYEBARAN DATA

17. UKURAN PENYEBARAN DATA
Simpangan rata-rata dari sekumpulan bilangan adalah:
nilai rata-rata hitung harga mutlak simpangan-simpangannya.
n
xx 
Hal.: 17STATISTIK
a. Data tunggal
SR =
Contoh :
Nilai ulangan matamatika dari 6 siswa adalah :7,5,6,3,8,7.
Tentukan simpangan rata-ratanya!
2. Simpangan Rata-rata

18. Jawab:
=
= 6
SR =
=
= 1,33
x 6
783657 
Hal.: 18STATISTIK
6
8
6
676863666567 
UKURAN PENYEBARAN DATA

19. b. Data berbobot / data
kelompok
SR =
x = data ke-i (data berbobot )
= titik tengah kelas interval ke-i (data kelompok )
f = frekuensi

 
f
xxf
Hal.: 19STATISTIK
UKURAN PENYEBARAN DATA

20. UKURAN PENYEBARAN DATA
Contoh :
Tentukan simpangan rata-rata dari data berikut :
Data Frekwensi x
3 – 5 2 4
6 – 8 4 7
9 – 11 8 10
12 - 14 6 13
Jumlah 20
Hal.: 20STATISTIK

21. UKURAN PENYEBARAN DATA
Jawab :
Frekwens
i
x
3 – 5 2 4
6 – 8 4 7
9 – 11 8 10
12 - 14 6 13
Jumlah 20
Hal.: 21STATISTIK
F . x xx  F xx 
8
28
80
78
x 

f
xf .
20
194
=
=
194
5,7
2,7
0,3
3,3
11,4
10,8
2,4
19,8
44,4

 
f
xxf
20
4,44
SR =
= = 2,22
= 9,7

22. Varians
(𝒔 𝟐 𝒂𝒕𝒂𝒖 𝝈 𝟐) Varians merupakanjumlahkuadratsemuadeviasinilai-
nilaiindividuterhadap rata-rata kelompok
 Varian di simbolkan :
𝝈 𝟐 = untukpopulasi
𝒔 𝟐 = untuksampel
 Akardarivariansdisebutstandardeviasiatausimpanganbaku
 Simpanganbakuataustandardeviasidisimbolkan:
𝝈= untukpopulasi
𝒔 = untuksampel

23. Rumus
𝝈 =
∑(𝒙𝒊 − 𝒙) 𝟐
𝒏
𝒔 =
∑𝒇(𝒙𝒊 − 𝒙) 𝟐
(𝒏 − 𝟏)
𝝈 𝟐 =
∑(𝒙𝒊 − 𝒙) 𝟐
𝒏
𝒔 𝟐
=
∑𝒇(𝒙𝒊 − 𝒙) 𝟐
𝒏 − 𝟏
Untuk Populasi
Untuk Data Sampel
Varians Standar Deviasi (simpangan
Baku)
Varians Standar Deviasi (simpangan
Baku)

24. Contoh :
Terdapat data sebagai
berikut :60, 70, 65, 80, 70, 65, 75, 80, 70, 75
Hitunglah Standar deviasi (simpangan bakunya) ?
1
2
3
4
5
6
7
8
9
10
n=10
No
75 4 16
75 4 16
710 0 390
65 -6 36
70 -1 1
80 9 81
80 9 81
70 -1 1
70 -1 1
65 -6 36
Nilai
Simpangan Simpangan Kuadrat
60 -11 121
710
10 = 71x =
(𝒙𝒊 −𝒙)²(𝒙𝒊 −𝒙)
∑(𝒙𝒊 − 𝒙)²
 Karena data disamping
merupakan data
Populasi maka kita
gunakan rumus:
𝝈 =
∑(𝒙𝒊 − 𝒙) 𝟐
𝒏

25. SEKIAN
DAN
TERIMAKASIH