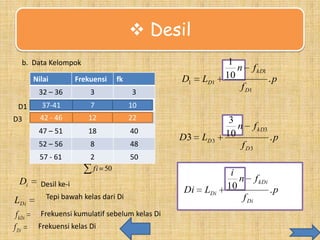
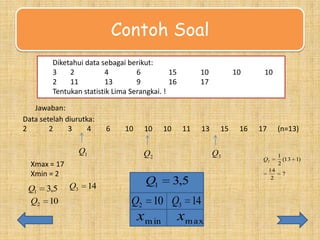
Dokumen ini membahas konsep dasar statistik, khususnya ukuran letak kumpulan data seperti kuartil dan desil, beserta cara menghitungnya dengan contoh soal. Terdapat penjelasan tentang data tunggal dan data kelompok, serta teknik interpolasi untuk mendapatkan nilai desil. Selain itu, juga dijelaskan tentang statistik lima serangkai yang terdiri dari nilai minimum, maksimum, dan kuartil.

1. STATISTIKA
AYO
BELAJAR BARENG
Oleh :
Aisa Nur Endahwati
102143809
JANGAN LUPA
DIPERHATIKAN
DAN DICATAT

2. Ukuran Letak Kumpulan Data
Macam Ukuran Letak Kumpulan Data
 Kuartil
 Desil

3.  Kuartil
b. Data Tunggal ( Data diurutkan)
Q1
Q2=Median
Q3
1
( n 1)
4
2
(n 1)
4
3
(n 1)
4
Qi
i
(n 1)
4

4. Contoh Soal
Diketahui data tersebar dengan susunan :
2, 4,6,9,10,10,11
Tentukan Q1, Q2 dan Q3 nya !
Jawaban:
2
4
Q1
Q2
Me
6
9
Q2
2
1
(n 1) (n 1)
4
2
10 10 11 ( n = 7 ganjil )
Q3
1
(7 1)
2
8
2
4

5. Contoh Soal
Diketahui data tersebar dengan susunan :
Tentukan Q1, Q2 dan Q3 nya !
Jawaban:
2
2
4
6
Q1
Q2
Me
9
10 10 10 11 13 15 16 17
Q3
Q2
2
1
(n 1) (n 1)
4
2
1
14
(13 1)
2
2
( n = 13 ganjil )
7
Statistika_Ukuran Pemusatan Data _ XI IPS _ Perhatikan dan Catat dengan baik ya_

6. Contoh Soal
Diketahui data tersebar dengan susunan :
2, 4,6,9,10,10,11,15
Tentukan Q1, Q2 dan Q3 nya !
Jawaban:
2
4
Q1
Q2
Me
6
9
10 10 11 15 ( n =8 genap )
Q3
Q2
2
1
(n 1) (n 1)
4
2
1
(8 1)
2
9
2
4,5

7.  Kuartil
b. Data Kelompok
Nilai
Frekuensi
fk
Q1
32 – 36
3
7
10
Q1
42 – 46
42 -
12
12
22
22
Q2
47 – 51
47 -
18
81
40
40
52 – 56
8
48
57 - 61
2
fi 50
50
Q1
LQ1
f kQ1
f Q1
Kuartil pertama/kuartil bawah
Tepi bawah kelas dari Q1
Frekuensi kumulatif sebelum kelas Q1
Frekuensi kelas Q1
Q1
41,5
f kQ1
f Q1
3
37 – 41
LQ1
1
n
4
.p
1
.50 10
4
.5
12
12,5 10
.5
12
2,5
41,5
.5
12
41,5
12,5
12
41,5 1,04
41,5
42,54

8.  Kuartil
b. Data Kelompok
Nilai
Frekuensi
fk
Q2
32 – 36
3
7
10
Q1
42 – 46
42 -
12
12
22
22
Q2
47 – 51
47 -
18
18
40
40
52 – 56
8
48
57 - 61
2
fi 50
50
Q2
LQ 2
f kQ2
fQ 2
Kuartil kedua/kuartil tengah/median
Tepi bawah kelas dari Q2
Frekuensi kumulatif sebelum kelas Q2
Frekuensi kelas Q2
Q2
46,5
f kQ2
fQ 2
3
37 – 41
LQ 2
2
n
4
.p
2
.50 22
4
.5
18
25 22
.5
18
3
46,5
.5
18
46,5
15
18
46,5 0,83
46,5
47,33

9.  Kuartil
b. Data Kelompok
Nilai
Frekuensi
fk
Q3
32 – 36
LQ 3
f kQ3
fQ3
42 – 46
42 -
12
12
22
22
47 – 51
47 -
18
18
40
40
8
48
57 - 61
Q3
10
52 – 56
Q3 Q2
7
2
fi 50
50
Kuartil ketiga/kuartil atas
Tepi bawah kelas dari Q3
Q3
46,5
.p
3
.50 22
4
.5
18
37,5 22
.5
18
15,5
46,5
.5
18
46,5
46,5
Frekuensi kumulatif sebelum kelas Q3
Frekuensi kelas Q3
f kQ3
fQ3
3
37 – 41
Q1
3
LQ 3
3
n
4
46,5
50,8
77,5
18
4,30

10.  Kuartil
b. Data Kelompok
Nilai
Frekuensi
fk
Q1
32 – 36
3
7
10
Q1
42 – 46
42 -
12
12
22
22
Q3 Q2
47 – 51
47 -
18
18
40
40
52 – 56
8
48
57 - 61
2
fi 50
LQ1
3
37 – 41
1
50 f kQ1
4
.p
f Q1
50
Qi
LQi
f kQi
f Qi
Kuartil ke-i
Q2
Q3
LQ 2
2
50 f kQ2
4
.p
fQ2
LQ 3
3
50 f kQ3
4
.p
fQ3
Tepi bawah kelas dari Qi
Frekuensi kumulatif sebelum kelas Qi
Frekuensi kelas Qi
Qi
LQi
i
n
4
f kQi
f Qi
.p

11. Contoh Soal
Carilah Q1,Q2 dan Q3 untuk data di bawah ini
Nilai
Frekuensi
1–5
2
6 – 10
3
11 – 15
10
16 - 20
5
Q1
Q2
Q3
Siapa Brani
Mencoba
Mengerjakan??
Yuk maju….

12. Q1
Nilai
Frekuensi
Fk
1–5
Q1
2
6 –61010
-
3
11 – 15
10
15
16 - 20
5
20
Q1
2
3
fi 20
5
5
LQ1
1
n
4
f kQ1
f Q1
1
.20 2
5,5 4
.5
3
5 2
5,5
.5
3
3
5,5
.5
3
5,5 5
10 ,5
.p

13. Q2
Nilai
Frekuensi Fk
1–5
2
6 – 10
Q2
2
3
5
11 – - 15
11 15
10 10
15 15
16 - 20
5
20
fi 20
Q2
LQ 2
2
n
4
f kQ2
fQ 2
2
.20 5
10,5 4
.5
10
10 5
10,5
.5
10
5
10,5
.5
10
10,5 2,5
13
.p

14. Q3
Nilai
1–5
2
2
6 – 10
Q2
Frekuensi(fi) Fk
3
5
11 11 – 15 15
10
16 - 20
5
3
n
4
10
15 15
20
fi 20
Q3
LQ 3
f kQ3
fQ3
.p
3
.20 5
10,5 4
.5
10
15 5
10,5
.5
10
10
10,5
.5
10
10 ,5 5
15,5

15.  Desil
a
9 buah nilai yang membagi data statistik jajaran / data yang sudah
diurutkan menjadi 10 bagian yang sama.
Desil ada 9 yaitu:
 Desil pertama
 Desil kedua
 Desil ketiga
 Desil keempat
 Desil kelima
 Desil keenam
 Desil ketujuh
 Desil kedelapan
 Desil kesembilan
dilambangkan dengan D1
dilambangkan dengan D2
dilambangkan dengan D3
dilambangkan dengan D4
dilambangkan dengan D5
dilambangkan dengan D6
dilambangkan dengan D7
dilambangkan dengan D8
dilambangkan dengan D9

16.  Desil
a
Cara menentukan nilai data desil ke-i :
1. Menentukan letak desil ke-i digunakan aturan letak desil ke – i yaitu
Di
i (n 1)
10
i 1 9
n banyaknyad
ata
2. Setelah letak desil ke i ditentukan selanjutnya nilai Desil ke – i
ditentukan menggunakan cara interpolasi linier
Memperkirakan sebuah nilai
diantara 2 buah nilai.

17. Contoh Soal
Dari data berikut:
4 , 3 , 9 , 13 , 7 , 9 , 15 , 8 , 17 , 20 , 11 , 25 , 22 ,16 , 18 , 5
Tentukan D1,D3,D5,D6 dan D8
Jawaban:
Statistika_Ukuran Pemusatan Data _ XI IPS _ Perhatikan dan Catat dengan baik ya_

18. Contoh Soal
Data yang telah diurutkan:
3 4
5
7
8
9
n = 16
 D1 = ...?
Letak D1 =
Nilai D1 =
1(16 1)
10
x1
9
17
10
0,7( x 2
11
13
1,7
x1 )
3 0,7(4 3)
3 0,7(4 3)
3 0,7 3,7
15
16
17
18
1,7 = 1 + 0,7
20
22
25

19. Contoh Soal
Data yang telah diurutkan:
3 4
5
7
8
9
n = 16
 D3 = ...?
Letak D3=
Nilai D3 =
3(16 1)
10
x5
9
51
10
0,7( x6
11
5,1
x5 )
8 0,1(9 8)
8 0,1
8,1
13
15
16
17
18
5,1 = 5 + 0,1
20
22
25

20. Contoh Soal
Data yang telah diurutkan:
3 4
5
7
8
9
n = 16
 D5 = ...?
Letak D5 =
Nilai D5 =
5(16 1)
10
x8
9
85
10
0,5( x9
11
13
8,5
15
16
17
8,5 = 8 + 0,5
x8 )
11 0,5(13 11)
11 0,5(2)
11 1 12
18
D5 = nilainya = Q2
20
22
25

21. Contoh Soal
Data yang telah diurutkan:
3 4
5
7
8
9
n = 16
 D6 = ...?
Letak D6 =
6(16 1)
10
Nilai D6 =
x10
9
102
10
0,2( x11
11
13
10,2
x10 )
15 0,2(16 15)
15 0,2
15,2
15
16
17
18
10,2 = 10 + 0,2
20
22
25

22. Contoh Soal
Data yang telah diurutkan:
3 4
5
7
8
9
n = 16
 D8 = ...?
Letak D8 =
8(16 1)
10
Nilai D8 =
x13
9
136
10
0,6( x14
11
13
13,6
x13 )
18 0,6(20 18)
18 0,6(2)
18 1,2 19,2
15
16
17
18
13,6 = 13 + 0,6
20
22
25

23.  Desil
b. Data Kelompok
Nilai
Frekuensi
fk
D1
32 – 36
7
10
10
12
22
18
40
52 – 56
8
48
57 - 61
LD1
f kD1
f D1
37 – 41
37-41
47 – 51
D1
3
42 – 46
D1
3
2
fi 50
50
Desil ke-1
Tepi bawah kelas dari D1
D1
1
n f kD1
LD1 10
.p
f D1
1
.50 3
36,5 10
.5
7
5 3
.5
7
2
36,5
.5
7
36,5
36,5
Frekuensi kumulatif sebelum kelas D1
Frekuensi kelas D1
36,5
37,2
10
7
0,7

24.  Desil
b. Data Kelompok
Nilai
Frekuensi
fk
32 – 36
LD 3
f kD3
f D3
7
10
10
42 42 – 46
12
22
22
18
40
8
48
57 - 61
D3
37 – 41
37-41
52 – 56
D3
3
47 – 51
D1
3
2
fi 50
50
Desil ke-3
Tepi bawah kelas 3ari D1
3
n f kD3
D3 LD 3 10
.p
f D3
3
.50 10
D 41,5 10
.5
12
15 10
.5
12
5
41,5
.5
12
41,5
41,5
Frekuensi kumulatif sebelum kelas D3
Frekuensi kelas D3
41,5
43,58
25
12
2,08

25.  Desil
LD1
1
n f kD1
10
.p
f D1
LD 3
3
n f kD3
10
.p
f D3
LDi
i
n f kDi
10
.p
f Di
b. Data Kelompok
Nilai
Frekuensi
D1
fk
32 – 36
LDi
f kDi
f Di
7
10
10
42 42 – 46
12
22
22
18
40
8
48
57 - 61
Di
37 – 41
37-41
52 – 56
D3
3
47 – 51
D1
3
2
fi 50
50
Desil ke-i
Tepi bawah kelas dari Di
Frekuensi kumulatif sebelum kelas Di
Frekuensi kelas Di
D3
Di

26.  Statistik Lima Serangkai
Q2
Q1
Xmin
Q3
Xmax

27. Contoh Soal
Diketahui data sebagai berikut:
3
2
4
6
15
2
11
13
9
16
Tentukan statistik Lima Serangkai. !
Jawaban:
Data setelah diurutka:
2
2
3
4
Q1
Q1 3,5
Q2 10
10
10
10
11
13
14
Q1
3,5
Q2 10 Q3 14
x m in
10
15
Q3
Q2
Xmax = 17
Xmin = 2
Q3
6
10
17
xm ax
16
10
17
(n=13)
Q2
14
2
1
(13 1)
2
7