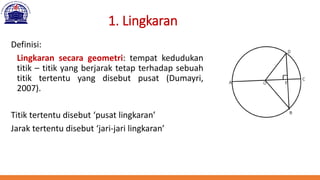
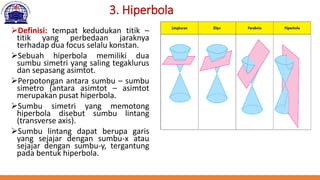
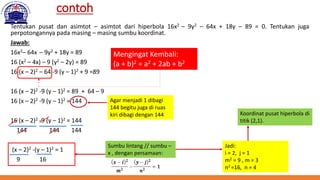
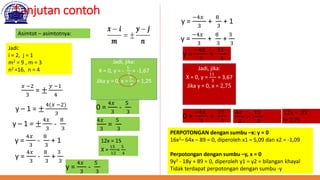
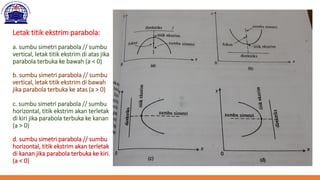
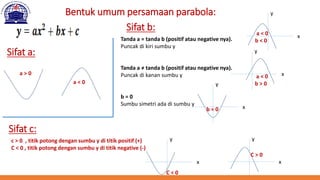
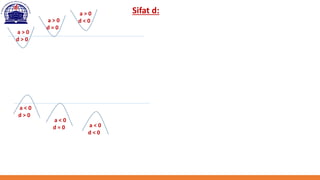
Dokumen ini membahas berbagai fungsi non-linear dalam analisis ekonomi, termasuk fungsi kuadrat, elips, hiperbola, dan parabola. Setiap fungsi diuraikan dengan definisi, bentuk umum, dan cara untuk menentukan pusat serta asimtot. Contoh konkret diberikan untuk menghitung titik ekstrim dan perpotongan dengan sumbu koordinat pada parabola.

1. Matematika Ekonomi
Persamaan Non Linear
Wiji Safitri, SMB., MM.
Program Studi Manajemen
Fakultas Ekonomi Bisnis dan Ilmu Sosial
Universitas Pelita Bangsa

2. FUNGSI NON LINEAR
Yang sering dijumpai dalam analisis ekonomi:
1. Fungsi Kuadrat Parabolik
2. Fungsi Kubik
3. Fungsi Eksponensial
4. Fungsi Logaritmik

3. Fungsi Kuadrat
Bentuk Umum Fungsi Kuadrat dg
dua variabel x dan y adalah:
Y = ax2+bx + c , a≠ 0
Gambar suatu fungsi dapat berupa
salah satu dari empat kemungkinan
bentuk potongan kerucut: lingkaran,
elips, hiperbola, dan parabola.

4. IDENTIFIKASI PERSAMAAN KUADRAT
Bentuk umum :
(setidak-tidaknya salah satu a atau b tidak sama dengan nol).
Dari bentuk yang lebih umum ini, dapat diidentifikasi gambar atau kurva dari
persamaannya, yaitu sbb:

5. Apabila p=0, dengan kata lain dalam persamaan kuadrat tersebut tidak terdapat suku
yang mengandung xy, bentuk yang lebih umum tadi menjadi :
Berdasarkan bentuk dengan kasus khusus ini, identifikasinya menjadi sbb:
✓ Jika a = b ≠ 0,kurvanya sebuah lingkaran
✓ Jika a ≠ b, tetapi bertanda sama, kurvanya sebuah elips
✓ Jika a dan b berlawanan tanda, kurvanya sebuah hiperbola
✓ Jika a = 0 atau b = 0, tetapi tidak keduanya, kurvanya sebuah parabola

6. 1. Lingkaran
Definisi:
Lingkaran secara geometri: tempat kedudukan
titik – titik yang berjarak tetap terhadap sebuah
titik tertentu yang disebut pusat (Dumayri,
2007).
Titik tertentu disebut ‘pusat lingkaran’
Jarak tertentu disebut ‘jari-jari lingkaran’

7. Bentuk Umum Persamaan Lingkaran:
Pusat dan jari-jari lingkaran dapat dicari dengan cara memanipulasi persamaan umum sedemikian rupa, sehingga :
• Dimana i dan j masing-masing adalah jarak pusat lingkaran terhadap sumbu-
sumbu y dan sumbu-sumbu horizontal x, r adalah jari-jari lingkaran.

8. 2. Elips
Definisi:
Elips adalah tempat kedudukan titik-titik yang jumlah
jaraknya terhadap dua focus selalu konstan.
sebuah elips mempunyai dua sumbu simetri yang saling
tegaklurus: yang Panjang disebut sumbu mayor,
sedangkan yang pendek disebut sumbu minor.
Fokus elips: sembarang titik yang terletak pada sumbu
elips. Titik potong antara sumbu – sumbu elips
merupakan pusat elips yang bersangkutan.

9. Bentuk Umum Persamaan Elips:
• Pusat dan jari-jari elips dapat dicari dengan cara memanipulasi persamaan umum sedemikian rupa, sehingga :
Dimana i dan j mencerminkan koordinat pusat elips serta r1 dan
r2 adalah jari-jarinya

10. 3. Hiperbola
➢Definisi: tempat kedudukan titik –
titik yang perbedaan jaraknya
terhadap dua focus selalu konstan.
➢Sebuah hiperbola memiliki dua
sumbu simetri yang saling tegaklurus
dan sepasang asimtot.
➢Perpotongan antara sumbu – sumbu
simetro (antara asimtot – asimtot
merupakan pusat hiperbola.
➢Sumbu simetri yang memotong
hiperbola disebut sumbu lintang
(transverse axis).
➢Sumbu lintang dapat berupa garis
yang sejajar dengan sumbu-x atau
sejajar dengan sumbu-y, tergantung
pada bentuk hiperbola.

11. Bentuk Umum Persamaan Hiperbola:
• Pusat hiperbola dapat dicari dengan
cara memanipulasi persamaan
umum sedemikian rupa, sehingga :
atau
Sumbu lintang // sumbu -x
Sumbu lintang // sumbu -y
a berlawanan tanda dengan b
Dimana i,j adalah koordinat
titik pusat hiperbolanya.

12. Persamaan untuk asimtot-asimtotnya dapat dicari melalui bentuk rumus
atau
Apabila m = n, asimtot –
asimtotnya akan saling
tegak lurus, sumbu
lintangnya tidak lagi
sejajar dengan salah satu
sumbu koordinat,
hiperbolanya disebut
hiperbola samasisi (equilateral
hyperbola).

13. contoh
Tentukan pusat dan asimtot – asimtot dari hiperbola 16x2 – 9y2 – 64x + 18y – 89 = 0. Tentukan juga
perpotongannya pada masing – masing sumbu koordinat.
Jawab:
16x2– 64x – 9y2 + 18y = 89
16 (x2 – 4x) – 9 (y2 – 2y) = 89
16 (x – 2)2 – 64 -9 (y – 1)2 + 9 =89
16 (x – 2)2 -9 (y – 1)2 = 89 + 64 – 9
16 (x – 2)2 -9 (y – 1)2 = 144
16 (x – 2)2 -9 (y – 1)2 = 144
144 144 144
(x – 2)2 -(y – 1)2 = 1
9 16
Agar menjadi 1 dibagi
144 begitu juga di ruas
kiri dibagi dengan 144
Mengingat Kembali:
(a + b)2 = a2 + 2ab + b2
Jadi:
i = 2, j = 1
m2 = 9 , m = 3
n2 =16, n = 4
Sumbu lintang // sumbu –
x , dengan persamaan:
Koordinat pusat hiperbola di
titik (2,1).

14. Lanjutan contoh
Asimtot – asimtotnya:
𝑥 −2
3
= ±
𝑦 −1
4
Jadi:
i = 2, j = 1
m2 = 9 , m = 3
n2 =16, n = 4
y – 1 = ±
4(𝑥 −2)
3
y – 1 = ±
4𝑥
3
-
8
3
y =
4𝑥
3
-
8
3
+ 1
y =
4𝑥
3
-
8
3
+
3
3
y =
4𝑥
3
-
5
3
y =
−4𝑥
3
+
8
3
+ 1
y =
−4𝑥
3
+
8
3
+
3
3
y =
−4𝑥
3
+
11
3
Jadi, jika:
X = 0, y = -
5
3
= -1,67
Jika y = 0, x =
5
4
= 1,25
0 =
4𝑥
3
-
5
3
4𝑥
3
=
5
3
12x = 15
X =
15
12
=
5
4
Jadi, jika:
X = 0, y =
11
3
= 3,67
Jika y = 0, x = 2,75
0 =
−4𝑥
3
+
11
3
4𝑥
3
=
11
3
12𝑥 = 33
X= 2,75
PERPOTONGAN dengan sumbu –x: y = 0
16x2– 64x – 89 = 0, diperoleh x1 = 5,09 dan x2 = -1,09
Perpotongan dengan sumbu –y, x = 0
9y2 - 18y + 89 = 0, diperoleh y1 = y2 = bilangan khayal
Tidak terdapat perpotongan dengan sumbu -y

15. 4. Parabola
✓Definisi: Parabola adalah tempat kedudukan
titik-titik yang berjarak sama terhadap sebuah
focus dan sebuah garis lurus yang disebut
direktriks.
✓Bentuk persamaan kuadrat yang paling penting
dalam penerapan bisnis dan ekonomi.
✓Setiap parabola memiliki sumbu simetri dan
sebuah titik ekstrim.
✓Sumbu simetri parabola dapat berupa garis yang
sejajar dengan sumbu vertical y atau berupa
yang sejajar dengan sumbu horizontal x.
✓Titik ekstrim parabola adalah titik potong antara
sumbu simetri dan parabola yang bersangkutan.

16. Letak titik ekstrim parabola:
a. sumbu simetri parabola // sumbu
vertical, letak titik ekstrim di atas jika
parabola terbuka ke bawah (a < 0)
b. sumbu simetri parabola // sumbu
vertical, letak titik ekstrim di bawah
jika parabola terbuka ke atas (a > 0)
c. sumbu simetri parabola // sumbu
horizontal, titik ekstrim akan terletak
di kiri jika parabola terbuka ke kanan
(a > 0)
d. sumbu simetri parabola // sumbu
horizontal, titik ekstrim akan terletak
di kanan jika parabola terbuka ke kiri.
(a < 0)

17. Bentuk umum persamaan parabola:
Atau
Sumbu simetri // sumbu vertikal Sumbu simetri // sumbu horizontal
✓ Untuk parabola, bentuk persamaan 1 parabolanya terbuka ke bawah jika a<0 dan terbuka ke atas jika a>0.
✓ Sedangkan untuk bentuk persamaan2 parabolanya terbuka ke kanan jika a>0 dan terbuka ke kiri jika a<0.
Titik ekstrim parabola (i , j) adalah :
Dimana -b/2a adalah jarak titik ekstrim dari sumbu vertikal y, sedangkan adalah jarak
titik ekstrim dari sumbu horizontal x.

18. Bentuk umum persamaan parabola:
Sifat a:
a > 0
a < 0
Sifat b:
Tanda a = tanda b (positif atau negative nya).
Puncak di kiri sumbu y
Tanda a ≠ tanda b (positif atau negative nya).
Puncak di kanan sumbu y
b = 0
Sumbu simetri ada di sumbu y
x
y
a < 0
b < 0
x
y
a < 0
b > 0
x
y
b = 0
Sifat c:
c > 0 , titik potong dengan sumbu y di titik positif (+)
C < 0 , titik potong dengan sumbu y di titik negative (-)
x
y
x
y
C < 0
C > 0

19. Sifat d:
a > 0
d > 0
a > 0
d = 0
a > 0
d < 0
a < 0
d > 0
a < 0
d = 0 a < 0
d < 0

20. Contoh
Tentukan titik ekstrim parabola y = x2 + 2X
–3 dan perpotongan dengan sumbu –
sumbu koordinat.
Jawab:
y = x2 + 2X –3
a = 1 > 0 oleh karena itu, parabola terbuka
ke ATAS dan titik ekstrim terletak di
BAWAH, berupa titik puncak. Dan sumbu
simetri // dengan sumbu vertical (lihat
rumus fungsinya)
Koordinat titik puncak:
= (
− 2
2
,
4+12
−4
) = (-1 , -4)
Perpotongan dengan sumbu –y :
jika x = 0
Y = - 3 kordinatnya (0, -3)
Perpotongan dengan sumbu x,
Jika Y = 0
y = x2 + 2X –3
0 = x2 + 2X –3
(x + 3 ) (x - 1 )= 0
X + 3 =0, X = -3
X – 1 = 0, X = 1
(-1, -4)
(1,0)(-3, 0)
(0, -3)
(SUMBUSIMETRI,X=-1)
X
Y

21. Latihan
1. Tentukan pusat dan asimtot – asimtot hiperbola:
a. 9x2 – 4y2 – 18x + 8y – 31 = 0
b. -9x2 + 4y2 + 36x – 24y = 0
2. Tentukan titik ekstrim dan keterbukaan parabola. Dan gambarkan
bentuk parabolanya pada sumbu x dan y:
a. Y = 3x2 – 30x + 77
b. Y = -5x2 + 30x - 35

22. Terima Kasih