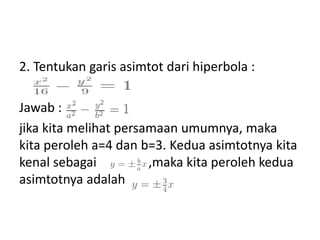
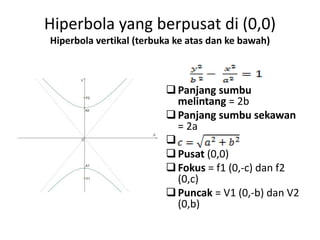
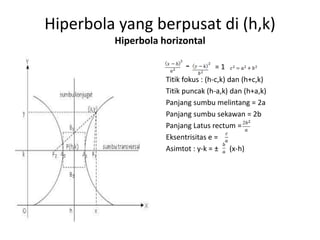
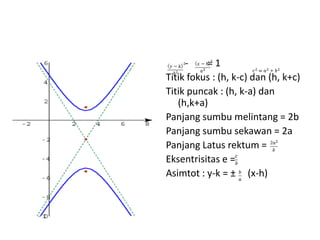
Dokumen tersebut membahas tentang hiperbola, yang merupakan kurva geometri tempat titik-titik yang selisih jaraknya terhadap dua titik tetap. Dokumen tersebut menjelaskan anggota kelompok, pengertian hiperbola, contoh soal, unsur-unsur hiperbola seperti fokus, puncak, asimtot, dan hiperbola yang berpusat pada titik tertentu.

1. Hiperbola
Anggota:
• Bella Rebecca
• Ilham Syukur H
• Laura Meity S
• Nurul Hasanah
• Silvia Oktavianti
• Simon Fetrus S

2. Pengertian
Hiperbola adalah tempat kedudukan titik-titik
yang selisih jaraknya terhadap dua titik
tertentu adalah tetap.

3. Hiperbola yang berpusat di (0,0)
Hiperbola horizontal (terbuka ke kiri dan ke kanan)
푥2
푎2-
푦2
푏2 = 1

4. Contoh soal
1. Tentukan kedua titik fokus dari hiperbola :
Jawab :
jika kita melihat persamaan umumnya, maka
kita peroleh a=4 dan b=3. dan kita dapatkan c=5.
Sehingga koordinat titik fokus dari hiperbola
tersebut adalah F1 (-5,0) (5,0)

5. 2. Tentukan garis asimtot dari hiperbola :
Jawab :
jika kita melihat persamaan umumnya, maka
kita peroleh a=4 dan b=3. Kedua asimtotnya kita
kenal sebagai , ,maka kita peroleh kedua
asimtotnya adalah

6. Hiperbola yang berpusat di (0,0)
Hiperbola vertikal (terbuka ke atas dan ke bawah)
 Panjang sumbu
melintang = 2b
 Panjang sumbu sekawan
= 2a

 Pusat (0,0)
 Fokus = f1 (0,-c) dan f2
(0,c)
 Puncak = V1 (0,-b) dan V2
(0,b)

7. Latus rectum (L)
Segmen garis yang dibatasi hiperbola, melalui
titik fokus dan tegak lurus sumbu mayor.
Hiperbola horizontal
Titik potong Latus rectum = (c, ) dan (c,- )
Panjang Latus rectum = 2
Hiperbola Vertikal
Titik potong Latus rectum = ( ,c) dan (- ,c)
Panjang Latus rectum = 2

8. Eksentrisitas (e) dan Asimtot
Hiperbola Horizontal
e = = = 2
Hiperbola Vertikal
e= = = 2
Hiperbola Horizontal
y = ± x
Hiperbola Vertikal
y = ± x

9. Hiperbola yang berpusat di (h,k)
Hiperbola horizontal
- = 1
Titik fokus : (h-c,k) dan (h+c,k)
Titik puncak (h-a,k) dan (h+a,k)
Panjang sumbu melintang = 2a
Panjang sumbu sekawan = 2b
Panjang Latus rectum =
Eksentrisitas e =
Asimtot : y-k = ± (x-h)

10. - = 1
Titik fokus : (h, k-c) dan (h, k+c)
Titik puncak : (h, k-a) dan
(h,k+a)
Panjang sumbu melintang = 2b
Panjang sumbu sekawan = 2a
Panjang Latus rektum =
Eksentrisitas e =
Asimtot : y-k = ± (x-h)