Downloaded 292 times
Uploaded byErvica Badiatuzzahra
Program linier – metode simpleks revisi (msr)
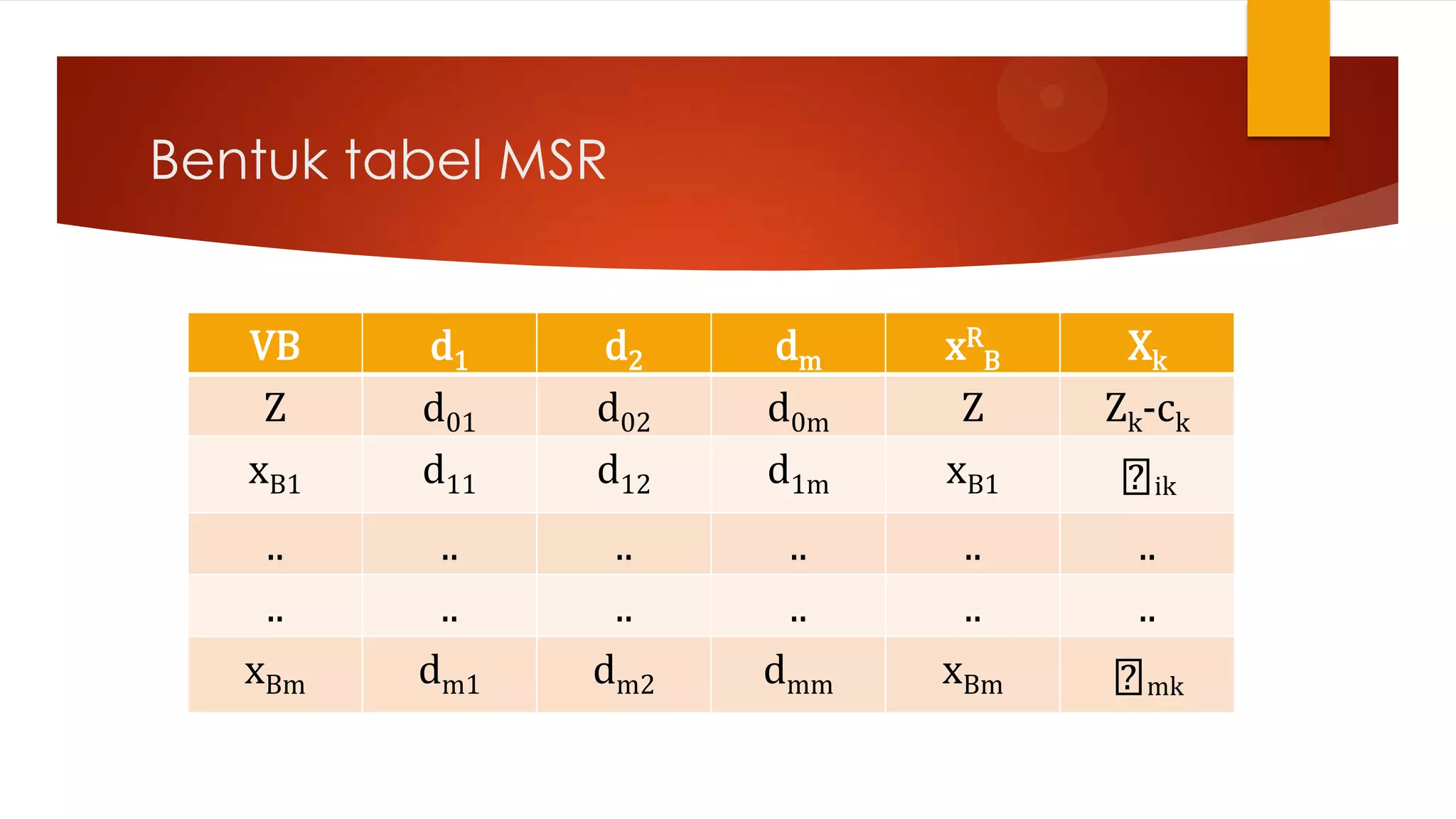
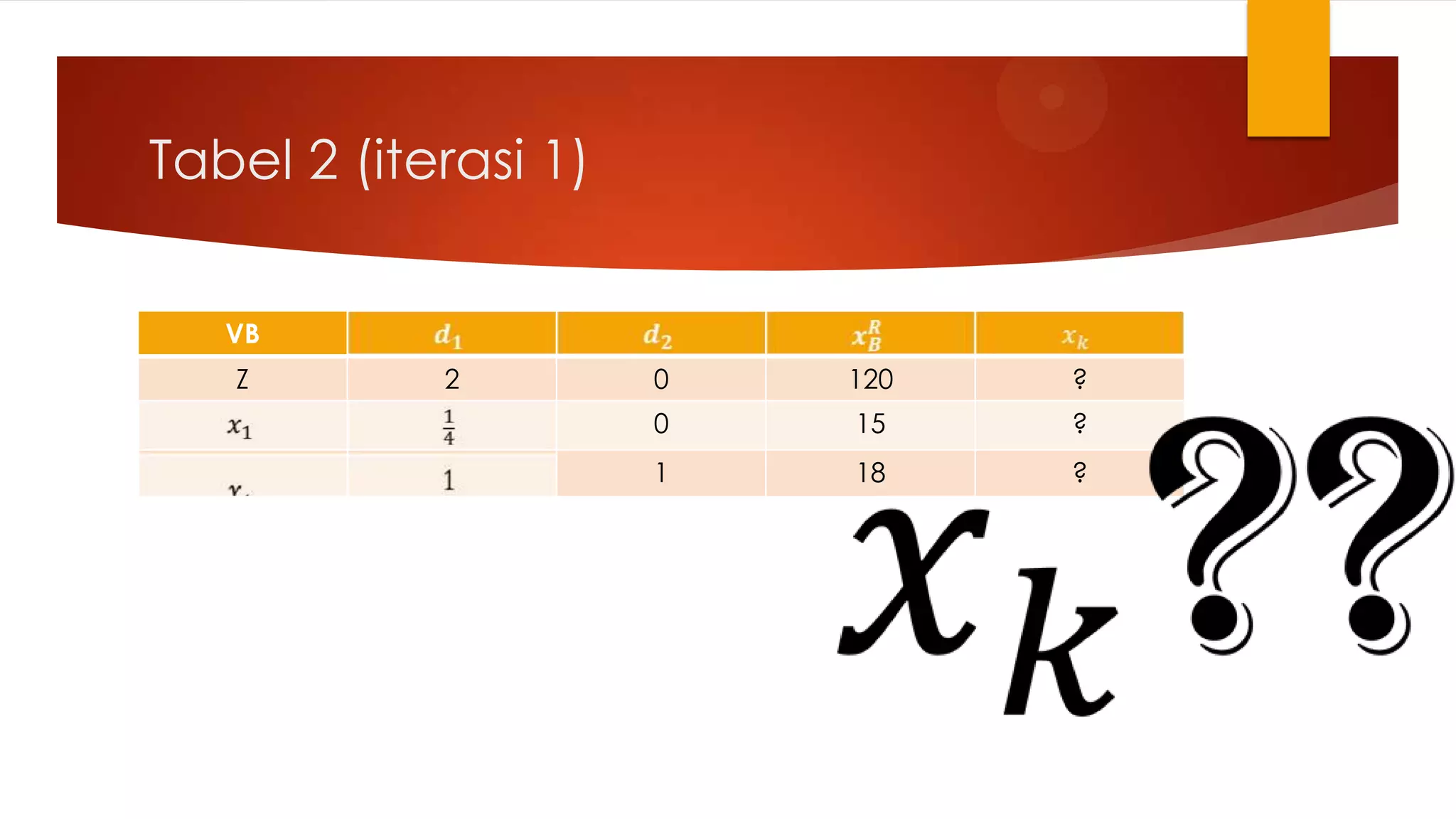
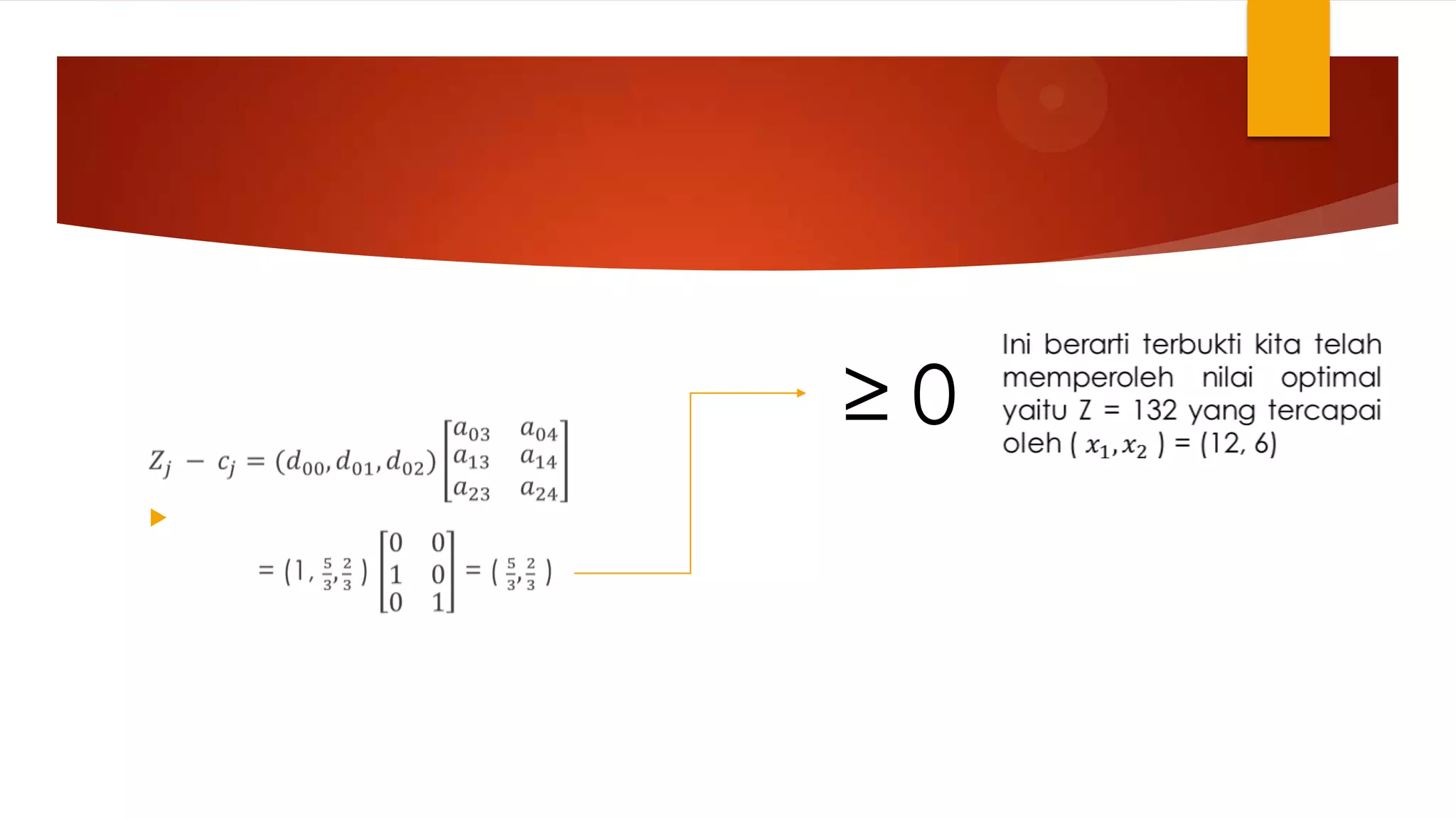
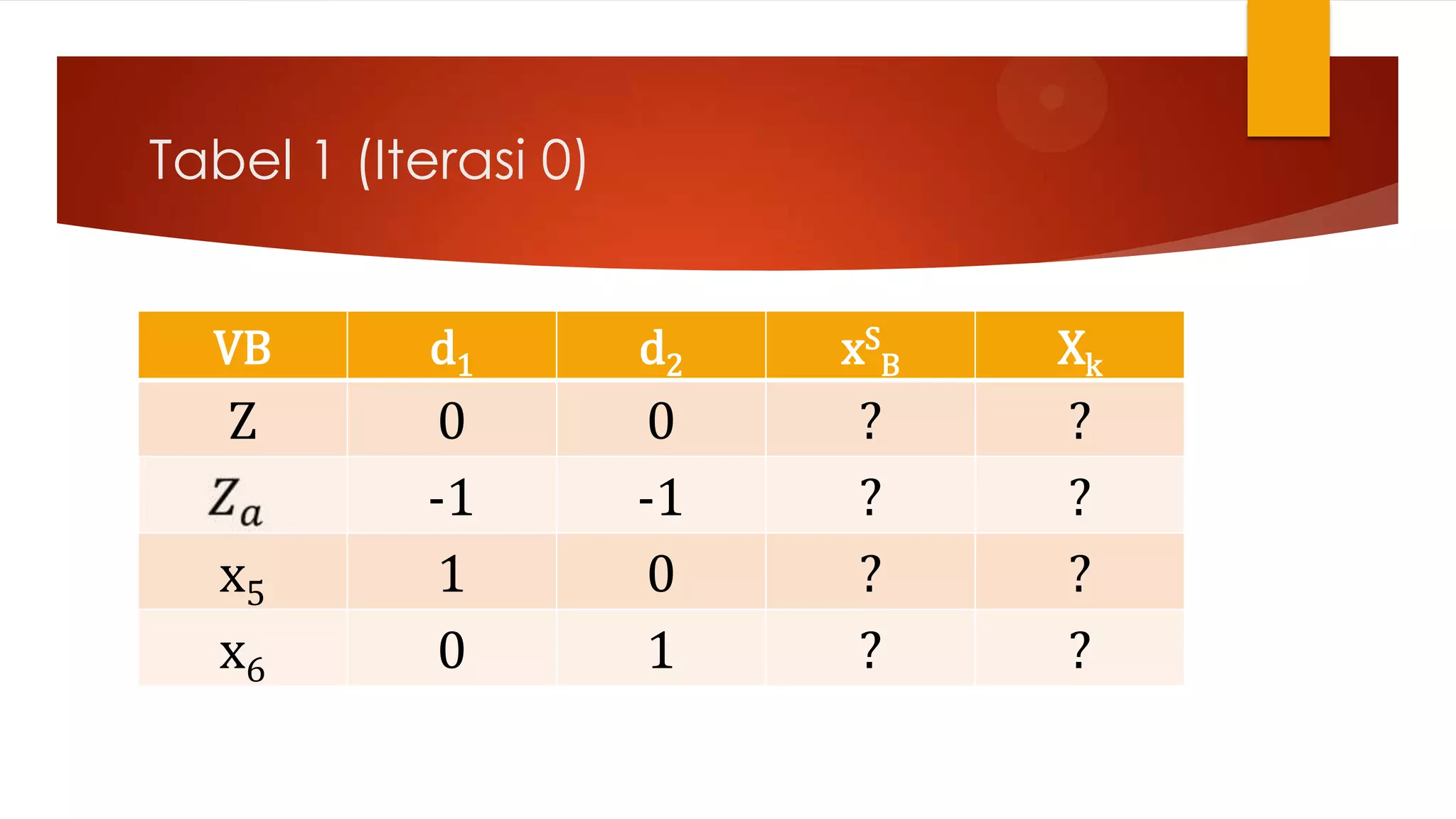
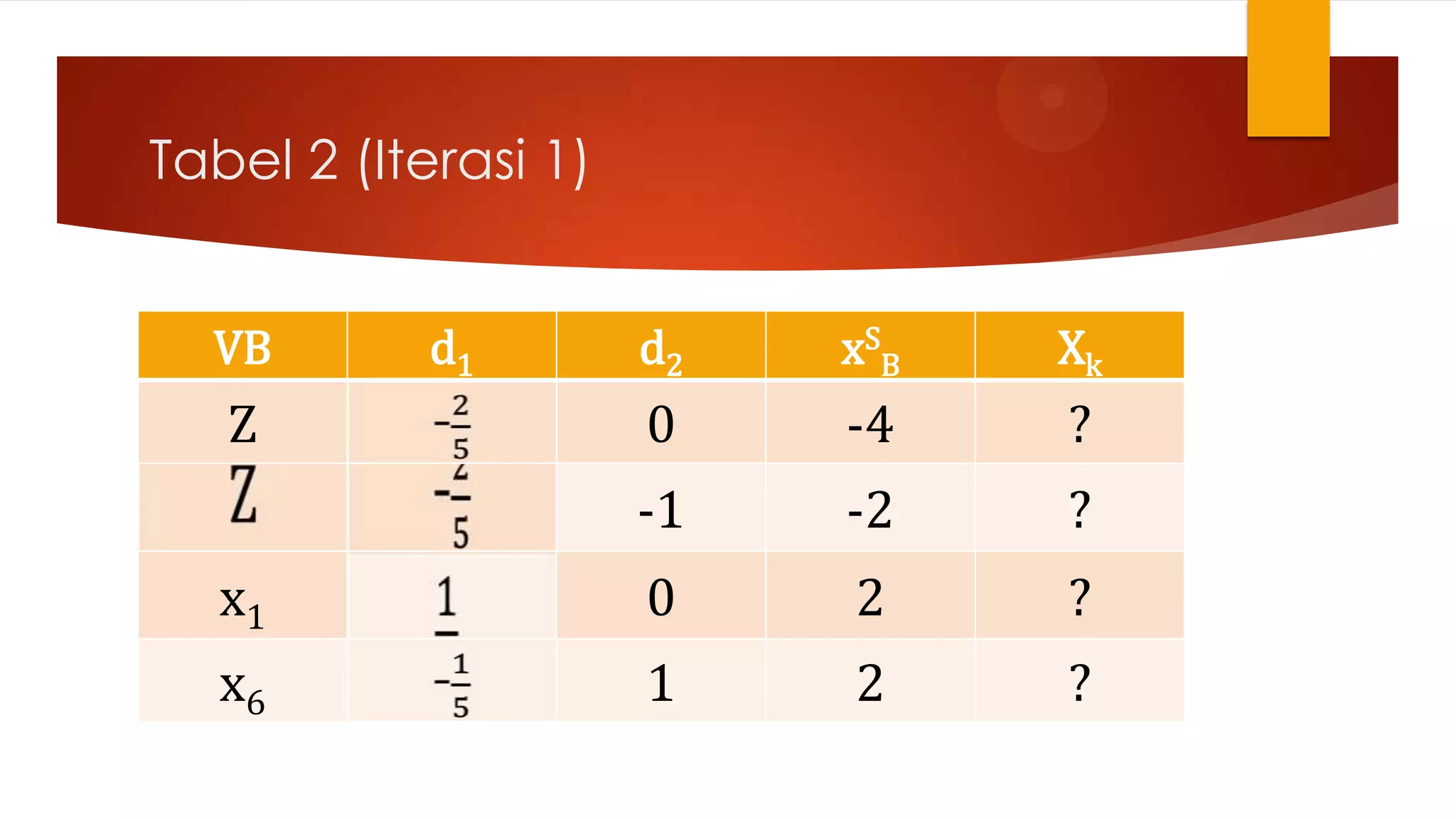
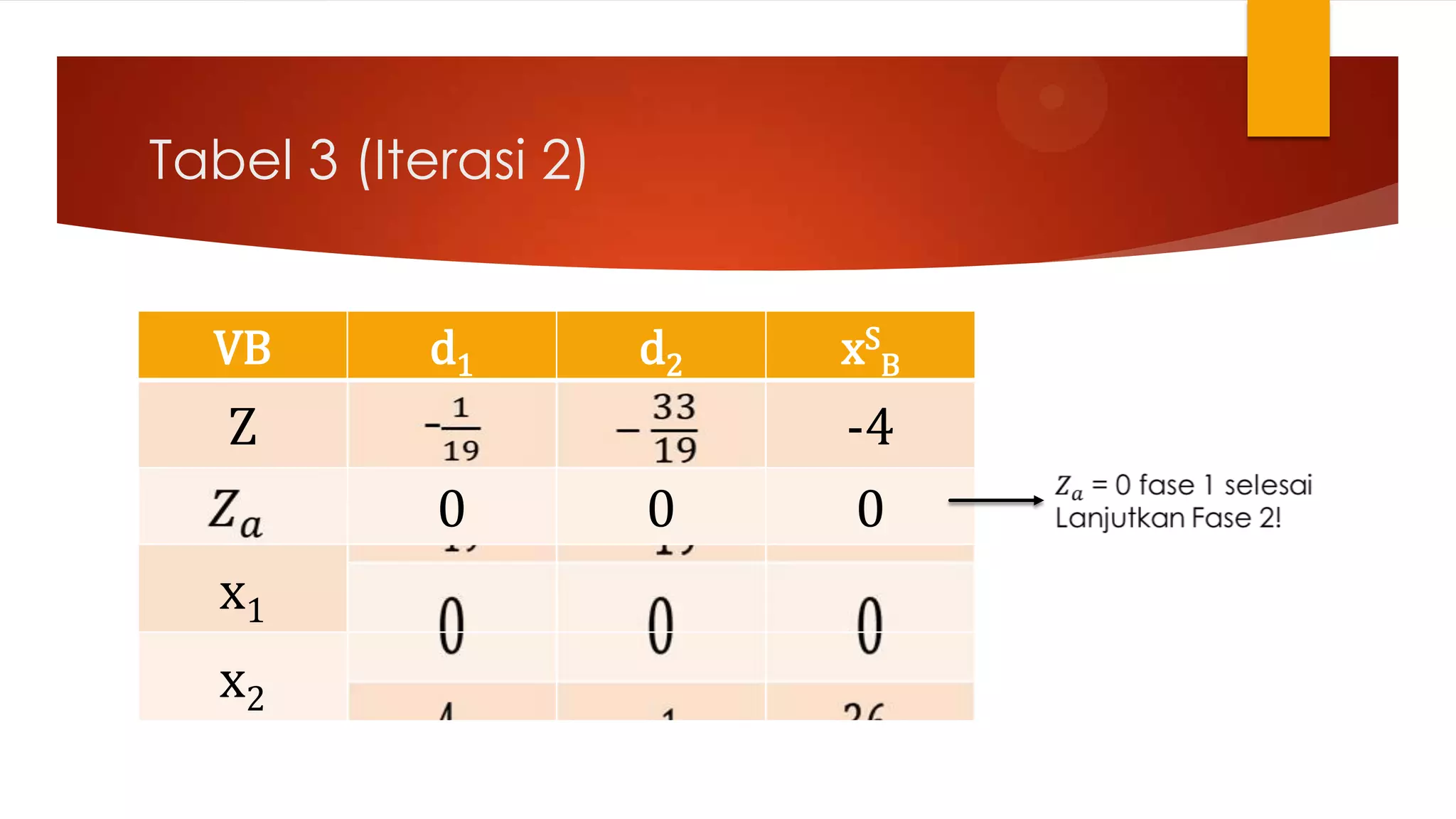
Dokumen tersebut membahas Metode Simpleks Revisi (MSR) untuk menyelesaikan masalah program linier. MSR merupakan penyederhanaan dari metode simpleks baku dengan hanya melakukan perhitungan konstanta yang dibutuhkan. MSR menggunakan tabel dan matriks yang lebih sederhana dibandingkan metode simpleks baku sehingga dapat menyelesaikan masalah program linier lebih cepat. Dokumen tersebut juga mendemonstrasikan langk
More Related Content
Similar to Program linier – metode simpleks revisi (msr)
Program linier – metode simpleks revisi (msr)
- 1. PROGRAM LINIER – METODESIMPLEKS REVISI (MSR) KELOMPOK 4 1. AZMAH AULIYA ACHMY ZAD 2. ERVICA BADIATU ZAHRA 3. EVA NADZIA 4. FAHMI SHIHHATUL AQDAH 5. KURNIA FAJARWATI 6. MAULUDIN HAFIZ AL-HADI
- 2. Metode Simpleks yangDirevisi Metode Simpleks yang Direvisi adalah penyederhanaan dari metode simpleks baku. Metode ini dikembangkan oleh Dantzig dan Oschard-Hays pada tahun 1953. Sentral perhatian dalam metode ini adalah perhitungan terhadap konstanta yang diperlukan saja.
- 3.
- 4.
- 5. Bentuk tabel MSR VB d1 d2 dm xRB Xk Z d01 d02 d0m Z Zk-ck xB1 d11 d12 d1m xB1 ᵝik .. .. .. .. .. .. .. .. .. .. .. .. xBm dm1 dm2 dmm xBm ᵝmk
- 6. Kelebihan MSR MSR melakukan perhitungan terhadap konstanta yang dibutuhkan saja. Tabel MSR lebih sederhana/simple. Dapat menggunakan matriks/vektor. Lebih cepat mendapatkan nilai optimal dari suatu fungsi tujuan.
- 7. Tahapan MSR (kasusmemaksimumkan Z tanpa variabel artifisial) 1. Tulis dalam bentuk matriks! 2. Buatlah tabel awal dan masukkan entri tabel, sisakan 1 kolom terakhir! 3. Carilah xk untuk menjadi variabel dasar 4. Carilah elemen pivot ᵝik dalam kolom terakhir tabel melalui cara yang lazim dari analisis simpleks baku 5. Gunakan persamaan transformasi yang umumnya digunakan dalam analisis simpleks baku untuk memperoleh semua masukan (entri) dalam tabel baru, kecuali kolom terakhir. 6. Ulangi langkah 3 sampai 5 sampai memperoleh Zj-cj > 0 untuk semua j.
- 8. Contoh : Selesaikan masalahberikut dengan MSR!! Maksimumkan Z = 8X1 + 6X2 Batasan : 4X1 + 2X2 ≤ 60 2X1 + 4X2 ≤ 48 X1, X2 ≥ 0
- 9. Solusi dengan MSR Masukanvariabel penambah (slack variable) X3 dan X4. Fungsi tujuan : Z – 8X1 – 6X2 + 0X3 + 0X4 = 0 Batasan : 4X1 + 2X2 + X3+ 0X4 = 60 2X1 + 4X2 + 0X3+ X4 = 48 X1, X2, X3, X4 ≥ 0 Sehingga diperoleh matriks sbb:
- 10. Buat tabel awal(iterasi 0) VB VB Z 0 0 0 ? Z 0 0 0 -8 1 0 60 ? 1 0 60 4* 0 1 48 ? 0 1 48 2
- 11. Tabel 2 (iterasi1) VB Z 2 0 120 ? 0 15 ? 1 18 ?
- 12. VB Z 2 0 120 -2 0 15 1 18 3*
- 13. Tabel 3 (iterasi2) VB Z 132 ? 12 ? 6 ?
- 14.
- 15. Tahapan MSR (kasusmeminimumkan Z dengan variabel artifisial) 1. Tulis dalam bentuk matriks! 2. Buatlah tabel awal dan masukkan entri tabel, sisakan 1 kolom terakhir! 3. Carilah xk untuk menjadi variabel dasar 4. Carilah elemen pivot ᵝik dalam kolom terakhir tabel melalui cara yang lazim dari analisis simpleks baku 5. Gunakan persamaan transformasi yang umumnya digunakan dalam analisis simpleks baku untuk memperoleh semua masukan (entri) dalam tabel baru, kecuali kolom terakhir. 6. Ulangi langkah 3 sampai 5 sampai memperoleh Zj-cj < 0 untuk semua j.
- 16. Contoh Selesaikan masalahberikut dengan MSR!! Minimumkan Z = 2X1 + 7X2 Batasan : 5X1 + X2 ≥ 10 X1 + 4X2 ≥ 4 X1, X2 ≥ 0
- 17.
- 18. Sajikan dalam bentukmatriks!
- 19.
- 20. Tabel 1 (Iterasi0) VB d1 d2 xSB Xk Z 0 0 ? ? -1 -1 ? ? x5 1 0 ? ? x6 0 1 ? ?
- 21. VB d1 d2 xSB Xk Z 0 0 0 ? -1 -1 -14 ? x5 1 0 10 ? x6 0 1 4 ?
- 22. VB d1 d2 xSB X1 Z 0 0 0 2 -1 -1 -14 -6 x5 1 0 10 5* x6 0 1 4 1
- 23. Tabel 2 (Iterasi1) VB d1 d2 xSB Xk Z 0 -4 ? -1 -2 ? x1 0 2 ? x6 1 2 ?
- 24. VB d1 d2 xSB X2 Z 0 -4 -1 -2 x1 0 2 x6 1 2
- 25. Tabel 3 (Iterasi2) VB d1 d2 xSB Z -4 0 0 0 x1 x2