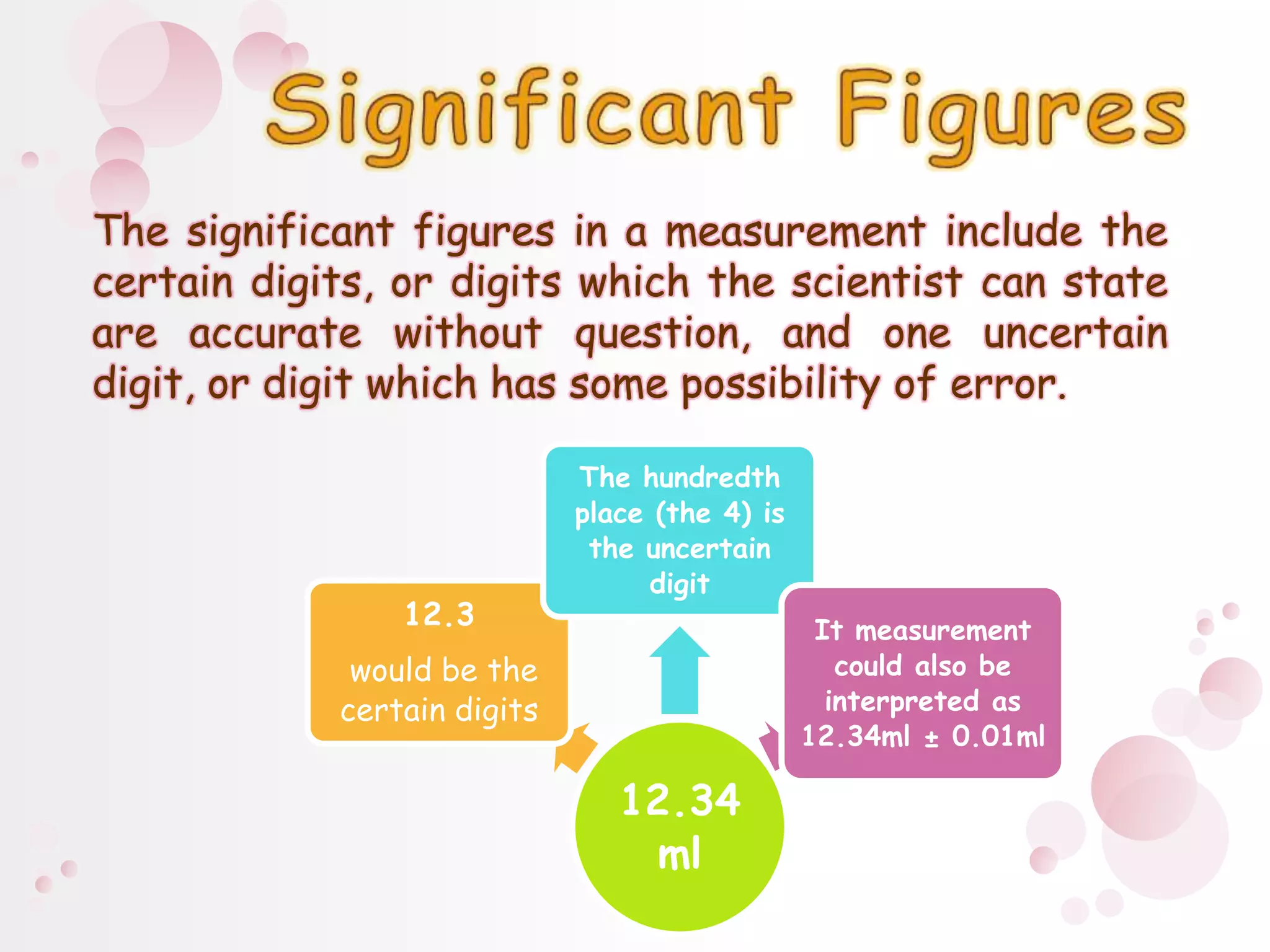
1) An approximation is an inexact representation of something that is still close enough to be useful as it reduces complexity while still yielding an accurate solution. 2) When performing calculations with approximations, the number of significant figures in the final result should match the least precise initial value. For addition/subtraction, round to the same decimal places, and for multiplication/division/roots round to the same number of significant figures. 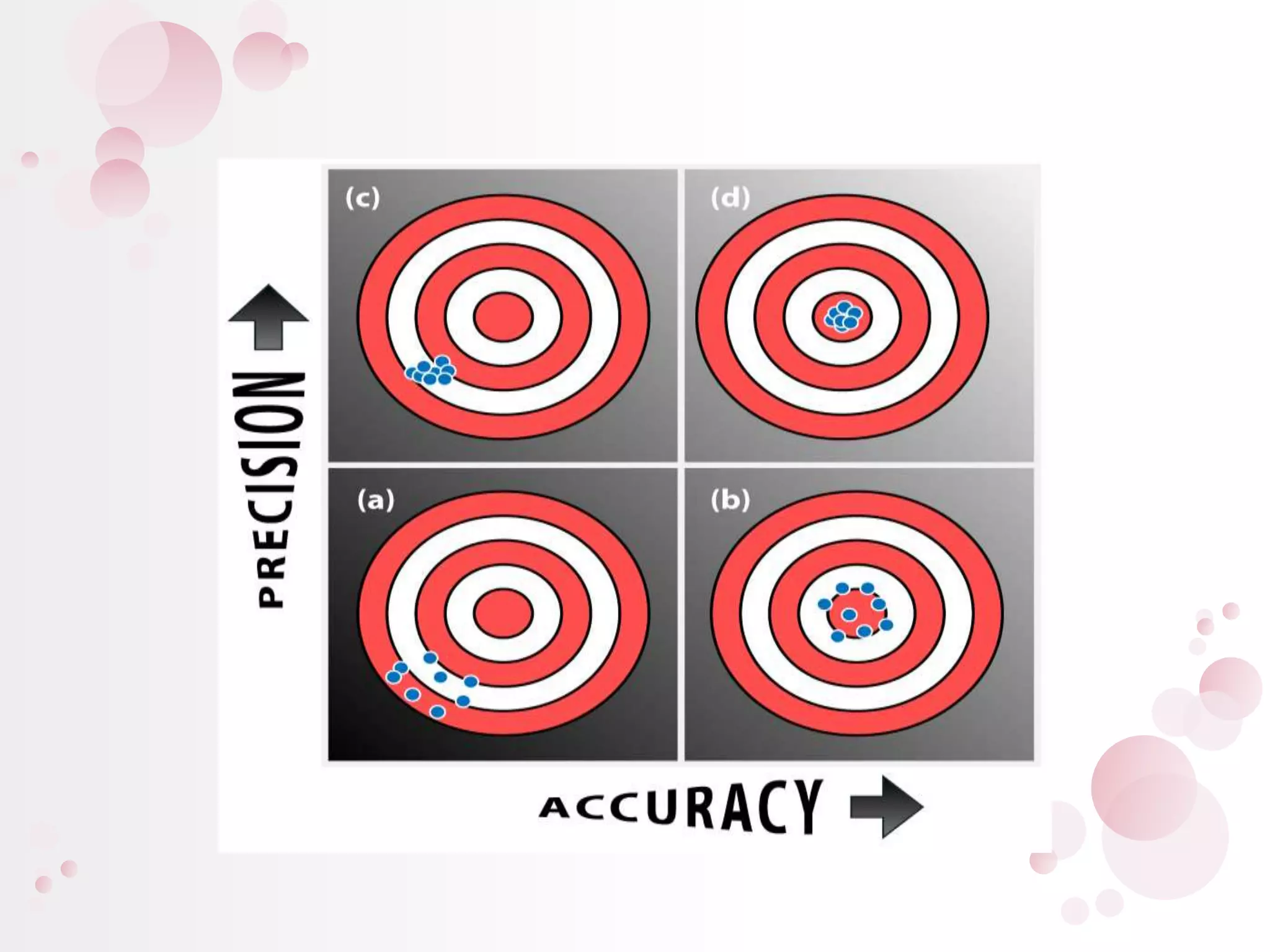3) Numerical errors are the difference between the true and approximate values. Relative percent error is used to normalize the error by the true value when measuring differences in magnitude. Rounding and truncation errors contribute to the total numerical error.

1. NUMERICAL APPROXIMATIONLizeth Paola Barrero RiañoPetroleumEngeenieringIndustrial University of Santander

2. DefinitionAn approximation is an inexact representation of something that is still close enough to be useful. It may yield a sufficiently accurate solution while reducing the complexity of the problem significantly.

3. SignificantFiguresThe significant figures in a measurement include the certain digits, or digits which the scientist can state are accurate without question, and one uncertain digit, or digit which has some possibility of error.

4. SignificantFigures

5. Particular situations

6. Particular situations

7. When adding and subtracting, round the final result to have the same precision (same number of decimal places) as the least precise initial value, regardless of the significant figures of any one term. 98.112 +2.300100.412 But this value must be rounded to 100.4 (the precision of the least precise term). Addition and Subtraction

8. When multiplying, dividing, or taking roots, the result should have the same number of significant figures as the least precise number in the calculation. 3.69 x 2.3059 8.5088This value which should be rounded to 8.51 (three significant figures like 3.69).Multiplication, Division, and Roots

9. Logarithms and AntilogarithmsWhen calculating the logarithm of a number, retain in the mantissa (the number to the right of the decimal point in the logarithm) the same number of significant figures as there are in the number whose logarithm is being found. This result should be rounded to 4.4771But this value should be rounded to 4.5

10. Logarithms and AntilogarithmsWhen calculating the antilogarithm of a number, the resulting value should have the same number of significant figures as the mantissa in the logarithm. antilog(0.301) = 1.9998, which should be rounded to 2.00antilog(0.301) = 1.9998, which should be rounded to 2.0

11. Accuracy and PrecisionNumerical methods must be sufficiently accurate or without bias to satisfy the requirements of a particular engineering problem

13. Numerical Errors

14. Numerical ErrorsTo both types of errors, the relation between the exact or real result and the approximate result is given by:True value = Approximate value + error Then the numerical error isEt = True value - Approximate valueWhere Etis used to denote the exact error value.

15. o This definition has the disadvantage of not taking into consideration the magnitude order of the estimated value, so an error of 1ft is much more significant if is measuring a bridge instead of the well depth. To correct this, the error is normalized with respect to the true value, i.e.:óReplacing in the above equation the true error Etis:

16. o Generally, in so much real applications are unknown the true answer, whereby is used the approximation:There are numerical methods which use iterative method to calculate the results, where do an approximation considering the previous approximation; this process is performed several times or iteratively, hoping for better approaches, therefore the relative percent error is given by:

17. Rounding Is the process of elimination of insignificant figures.

18. Rounding

19. Total Numerical ErrorIt is the addition of the truncation and rounding errors. The only way to minimize this type of error is to increase the number of significant figures.

20. Truncation error and Taylor’s series

21. o Taylor’s seriesTo the Taylor‘s series construction makes use of approximations, what allows us to understand more about them. Initially requires a first term which is a zero-order approximation:f value at the new point is equal to the value in the previous pointIf (xi)is next to (xi+1),then f(xi) soon will be equal to F(xi+1):

22. o To achieve greater approach adds one more term to the series; this is an order 1 approximation, which generates an adjustment for straight lines.To make the Taylor ’series expansion and to gain better approach generalizes the series for all functions, as follows:

23. BibliographyCHAPRA, Steven C. y CANALE, Raymond P.: Métodos Numéricos para Ingenieros. McGraw Hill 2007. 5ª edition.http://en.wikipedia.org/wiki/Approximationhttp://www.mitecnologico.com/Main/ConceptosBasicosMetodosNumericosCifraSignificativaPrecisionExactitudIncertidumbreYSesgohttp://www.ndt-d.org/GeneralResources/SigFigs/SigFigs.htmhttp://www.montgomerycollege.edu/Departments/scilcgt/sig-figs.pdf