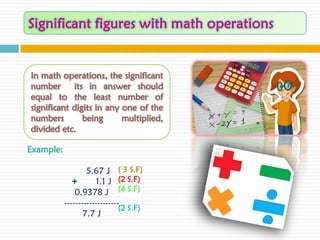
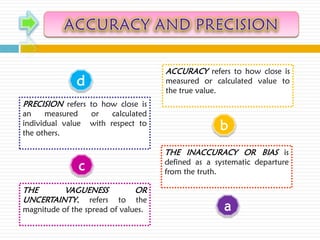
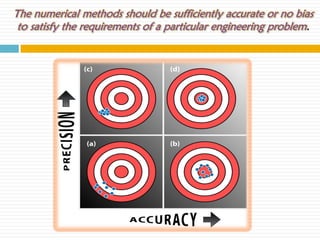
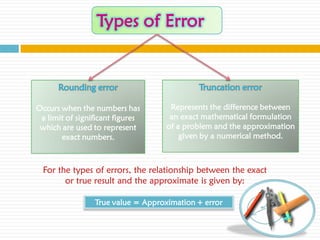
The document discusses numerical approximation and significant figures. It begins by explaining what significant figures are and how they are used to determine the accuracy of measurements. It then provides examples of measurements with different numbers of significant figures. The main points are that numerical methods provide approximate results, and significant figures are used to specify the accuracy of those results in terms of the number of figures that can be reliably used.

2. NUMERICAL
APPROXIMATION

3. The concept of significant
figures has been
developed to designate
formally the reliability of a
numerical value. The
significant figures of a
number are those that can
be used reliably, e.g, used
to determine the accuracy
of the measurement.

4. The measurement of fluid
volume in the graduated
cylinder is between 38
and 39 cm³. We believe
that it is 38.4 cm or 38.2
cm³. As modified, a move
the last digit is estimated
and therefore
uncertain. The measure of
this volume has three
significant figures.

5. The concept of significant figures has two important implications for
the study of numerical methods.
1
The numerical methods obtain approximate
results. Therefore, we must develop criteria to
specify how accurate are the results
obtained. A way to do it is in terms of
significant figures. For example, we can say
that the approach is acceptable to four
significant figures.

6. 2
Although certain quantities such as π or e
represent specific numbers, they can’t to
express exactly with a finite number of digits.
For example:
π = 3.14159265358973238462643... To
infinity.
The computers hold only a finite number of
significant figures, these numbers can never be
represented accurately.

7. 1 All nonzero digits are significant:
1,284 g  4 significant figures
1,2 g  2 significant figures
With zeroes, the situation is particularly:
Zeroes placed before other digits are
2 not significant.
0.046  2 significant digits.

8. 3 Zeroes placed between other digits are
always significant.
4009 kg  4 significant digits.
Zeroes placed after other digits
4 but behind a decimal point are
significant.
7,90  3 significant digits.

9. 5 Zeroes at the end of a number
are significant only if they are
behind a decimal point.
Otherwise, it is impossible to
tell if they are significant. For
example, in the number 8200,
it is not clear if the zeroes are
significant or not. The number
of significant digits in 8200 is at
least two, but could be three or
four. To avoid uncertainty, use
scientific notation to place 8.200 x 103  4 S.F
significant zeroes behind a
decimal point: 8.20 x 103  3 S.F
8.2 x 103  2 S.F

10. In math operations, the significant
number its in answer should
equal to the least number of
significant digits in any one of the
numbers being multiplied,
divided etc.
Example:
5.67 J ( 3 S.F)
+ 1.1 J (2 S.F)
0.9378 J (4 S.F)
--------------------
(2 S.F)
7.7 J

11. It's called rounding to the process of eliminating non-significant digits
of a number. The rules are the following:
1 If the digit removed is greater than 5, the previous
digit increases by one. E.g: 8.236 → 8.24
If the digit removed is less than 5, the previous digit
2 is not modified. E.g: 8.231 → 8.23
If the digit removed is 5 followed by a different
3 number than 0, the previous digit increases by one.
E.g: 8.2353→8.24
If the digit removed is 5 followed by 0 looks to the
4 next that follows, if it is odd increase or if it’s pair
remains unchanged. E.g: (1) 8.23503→8.24
(2) 8.23502→8.23

12. 1. Writing more digits in an
answer (intermediate or final)
than justified by the number of
digits in the data.
2. Rounding-off, say, to two
digits in an intermediate answer,
and then writing three digits in
the final answer.

13. ACCURACY refers to how close is
d measured or calculated value to
the true value.
PRECISION refers to how close is
an measured or calculated
individual value
the others.
with respect to
b
THE INACCURACY OR BIAS is
c defined as a systematic departure
from the truth.
THE VAGUENESS OR
UNCERTAINTY, refers to the
magnitude of the spread of values. a

14. The numerical methods should be sufficiently accurate or no bias
to satisfy the requirements of a particular engineering problem.

16. Rounding error Truncation error
Occurs when the numbers has Represents the difference between
a limit of significant figures an exact mathematical formulation
which are used to represent of a problem and the approximation
exact numbers. given by a numerical method.
For the types of errors, the relationship between the exact
or true result and the approximate is given by:
True value = Approximation + error

17. • True or Absolute Error
It is equal to the difference between the true value and
approximate value
• Relative Error
It is the quotient (division) between the absolute error and
the true value. If you multiply by 100 to obtain the true
percentage relative error.
True Value - Approximation True Value - Approximation
Relative Error=
True Value or t = x100
True Value

18. For numerical methods, the true value will only be known when the
functions can be solved analytically. Thus, in real life to know the true
value early, it is difficult. In these cases, normalizing the error is an
alternative to have the best possible estimate of true value:
Approximate Error
a= x100
Approximate Value
Some numerical methods use an iterative method to calculate results. In
such cases, the error is calculated as the difference between the previous
and the current approach. Therefore, the percentage relative error is
given by:
Current approach - Anterior approach
a= x100
Current approach

20. In essence, the Taylor series
provides a means to predict
the value of a function at a
point in terms of the
function value and its
derivatives at another
point. In particular, the
theorem states that any
smooth function can be
Aproximación de la función exponencial approximated with a
Fuente:
http://upload.wikimedia.org/wikipedia/commo polynomial.
ns/6/64/Taylorspolynomialexbig.svg

21. To the Taylor’s series construction makes use of
approximations, what allows us to understand more
about them.
Initially requires a first term which is a zero-order
approximation
(f value at the new point is equal to the value in the
previous point)
If (xi ) is next to (xi+1),then F(xi) soon will be equal
to F(xi+1):

22. To achieve greater approach adds one more term to
the series; this is an order 1 approximation, which
generates an adjustment for straight lines.
To make the Taylor´s series expansion and to gain
better approach generalizes the series for all functions,
as follows:

23. Similarly can be added terms and obtain the Taylor series of order n:
f ''(a ) f ( n )(a )
f( x)  f(a )  f '(a )( x  a )  ( x  a )2  ...  ( x  a )n  Rn
2! n!
Where Rn term is
included, to notice
the term of n +1 to
infinity. :
x
( x  t )n ( n1)
Rn   f (t )dt
a n!
“With the Taylor’ series we can estimate the truncation errors”