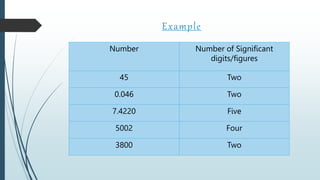
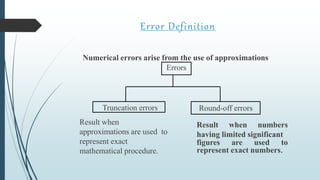
The document discusses numerical methods, focusing on approximation and error, highlighting the inherent inaccuracies in measurements and algorithms. It details significant figures, types of errors such as truncation and round-off, and definitions of true error and relative error. Additionally, it emphasizes the challenges of working with approximations in mathematical computations.

1. Topic: Approximation and Error
Name: Ayan Das
Dept: CSE Sem: 6th
Year: 3rd
Subject: Numerical Methods Subject Code: OEC-IT601A
Roll No: 25300121057 Reg No: 212530100120005
Supreme Knowledge Foundation Group
Of Institutions

2. • Numerical methods yield approximate results, results that
are close to the exact analytical solution.
– Only rarely given data are exact, since they originate
from measurements. Therefore there is probably error in
the input information.
– Algorithm itself usually introduces errors as well, e.g.,
unavoidable round-offs, etc …
– The output information will then contain error from both of these
sources.

3. Significant Figure
Accuracy and Precision
Error
Taylor Series
Types of Approximation and Error

4. S i g n i f i c a n t F i g u r e
Significant figures of a number are those that can be used with confidence.
 Rules for identifying sig. figures:
• All non-zero digits are considered significant. For example, 91 has two significant digits (9
and 1), while 123.45 has five significant digits (1, 2, 3, 4 and 5).
• Zeros appearing anywhere between two non-zero digits are significant. Example:
101.12 has five significant digits.
• Leading zeros are not significant. For example, 0.00052 has two significant digits
• Trailing zeros are generally considered as significant. For example, 12.2300 has six
significant digits.

5. Example
Number Number of Significant
digits/figures
45 Two
0.046 Two
7.4220 Five
5002 Four
3800 Two

6. 53,800 How many significant figures?
5.38 x 104 3
5.380 x 104 4
5.3800 x 104 5
Zeros are sometimes used to locate the decimal point not significant
figures.
0.00001753 4
0.0001753 4
0.001753 4
Example

7. Error Definition
Truncation errors
Numerical errors arise from the use of approximations
Errors
Result when
approximations are used to
represent exact
mathematical procedure.
Result when numbers
having limited significant
figures are used to
represent exact numbers.
Round-off errors

8. Round-off Errors
 Numbers such as p, e, or cannot be expressed by a fixed number
of significant figures.
 Computers use a base-2 representation, they cannot precisely
represent certain exact base-10 numbers.
 Fractional quantities are typically represented in computer using
“floating point” form, e.g.,
Example:
  = 3.14159265358 to be stored carrying 7 significant digits.
  = 3.141592 chopping
  = 3.141593 rounding

9. Truncation Errors
Truncation errors are those that result using approximation
in place of an exact mathematical procedure.
dv

v

Vti1Vti 
dt t ti1ti
____________

10.  True error (Et)
True error (Et) or Exact value of error
= true value – approximated value
 True percent relative error ( )
t
true value
True value

true value  approximated value
100 (%)
t
True percent relative error   
Trueerror
100 (%)
True Error

11. Approximate Error
• The true error is known only when we deal with functions that can be solved
analytically.
• In many applications, a prior true value is rarely available.
• For this situation, an alternative is to calculate an approximation of the error using
the best available estimate of the true value as:
  Approximate percent relative error 
Approximate error
100 (%)

12. Thank You