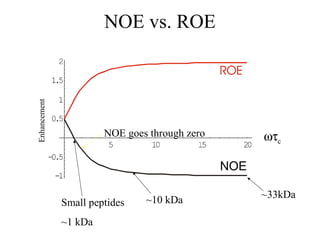
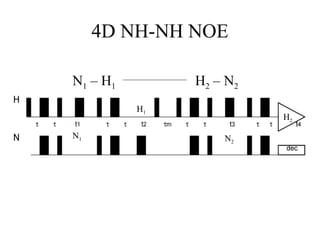
The nuclear Overhauser effect (NOE) is an incoherent cross-relaxation process between two nuclear spins within approximately 5 angstroms of each other. The intensity of the NOE is proportional to r-6, where r is the distance between the spins, meaning it decays very quickly with increasing distance. NOE experiments can provide distance restraints for structure determination of biological macromolecules like proteins.

1. NOE
•Transferring magnetization through scalar coupling is a
“coherent” process. This means that all of the spins are doing
the same thing at the same time.
•Relaxation is an “incoherent” process, because it is caused by
random fluxuations that are not coordinated.
•The nuclear Overhauser effect (NOE) is in incoherent process
in which two nuclear spins “cross-relax”. Recall that a single
spin can relax by T1 (longitudinal or spin-latice) or T2
(transverse or spin-spin) mechanisms. Nuclear spins can also
cross-relax through dipole-dipole interactions and other
mechanisms. This cross relaxation causes changes in one spin
through perturbations of the other spin.
•The NOE is dependent on many factors. The major factors
are molecular tumbling frequency and internuclear distance.
The intensity of the NOE is proportional to r-6 where r is the
distance between the 2 spins.

2. Qualitative Description
Two nuclear spins within about 5 Å will
interact with each other through
space. This interaction is called
cross-relaxation, and it gives rise to
the nuclear Overhauser effect
(NOE).
Two spins have 4 energy levels, and the
transitions along the edges
correspond to transitions of one or
the other spin alone. W2 and W0 are
the cross-relaxation pathways,
which depend on the tumbling of
the molecule.
2 spins I and S
aa n1(***)
(***) n2 ab
bb n4(*)
WS
(1)
WS
(2)
WI
(1)
WI
(2)
ba n3(*)
W2
W0

3. dn1/dt = -WS
(1)n1-WI
(1)n1–W2n1 + WS
(1)n2+WI
(1)n3+W2n4
… etc for n2,3,4
using: Iz= n1-n3+n2-n4 Sz= n1-n2+n3-n4 2IzSz= n1-n3-n2+n4
One gets the ‘master equation’ or Solomon equation
dIz/dt = -(WI
(1)+WI
(2)+W2+W0)Iz – (W2-W0)Sz –(WI
(1)-WI
(2))2IzSz
dSz/dt = -(WS
(1)+WS
(2)+W2+W0)Sz – (W2-W0)Iz – (WS
(1)-WS
(2))2IzSz
d2IzSz/dt = -(WI
(1)+WI
(2)+ WS
(1)+WS
(2))2IzSz - (WS
(1)-WS
(2))Sz - (WI
(1)-WI
(2))Iz
(WI
(2)+W2+W0) auto relaxation rate of Iz or rI
(1)+WI
(WS
(1)+WS
(2)+W2+W0) auto relaxation rate of Rz or rR
(W-W) cross relaxation rate s20IS
Terms with 2IzSz can be neglected in many circumstances
unless (W(1)-WI/S
I/S
(2)) (D-CSA ‘cross correlated relaxation’ etc …)

4. Spectral densities J(w)
W0 µ gI
2 gS
2 rIS
-6 tc / [ 1 + (wI - wS)2tc
2]
W2 µ gI
2 gS
-6 tc / [ 1 + (wI + wS)2tc
2 rIS
2]
WS µ gI
2 rIS
2 gS
-6 tc / [ 1 + wS
2tc
2]
WI µ gI
2 rIS
2 gS
-6 tc / [ 1 + wI
2]
2tc
• Since the probability of a transition depends on the different
frequencies that the system has (the spectral density), the
W terms are proportional the J(w).
• Also, since we need two magnetic dipoles to have dipolar
coupling, the NOE depends on the strength of the two
dipoles involved. The strength of a dipole is proportional to
rIS
-3, and the Ws will depend on rIS
-6:
for proteins only W0 is of importance W I,S,2 <<
• The relationship is to the inverse sixth power of rIS, which
means that the NOE decays very fast as we pull the two
nuclei away from each other.
• For protons, this means that we can see things which are at
most 5 to 6 Å apart in the molecule (under ideal conditions…).

5. d(Iz – Iz0)/dt = - rI (Iz–Iz0) - sIS (Sz–Sz0)
d(Sz – Sz0)/dt = - sIS (Iz–Iz0) - rS (Sz–Sz0)
Note that in general there is no simple
mono-exponential T1 behaviour !!

6. Steady State NOE Experiment
For a ‘steady state’ with Sz saturation Sz=0
d(IzSS – Iz0)/dt = - rI (IzSS–Iz0) - sIS (0–Sz0) = 0
IzSS = sIS/rI Sz0 + Iz0
for the NOE enhancement
h=(IzSS-Iz0)/ Iz0= sIS/rI Sz0/Iz0

7. NOE difference
Ultrahigh quality NOE spectra: The upper spectrum shows the NOE enhancements observed when
H 5 is irradiated. The NOE spectrum has been recorded using a new technique in which pulsed
field gradients are used; the result is a spectrum of exceptional quality. In the example shown here,
it is possible to detect the enhancement of H10 which comes from a three step transfer via H6 and
H9.
One-dimensional NOE experiments using pulsed field gradients, J. Magn. Reson., 1997, 125, 302.

8. Transient NOE experiment
Solve the Solomon equation
With the initial condition
Iz(0)=Iz0 Sz(0)=-Sz0
For small mixing times tm
the ‘linear approximation’ applies:
d(Iz(t)– Iz0)/dt = -r(Iz(t)–Iz0) - s(Sz–Sz0) ~ 2 sSz0
IISISValid for trand ts<< 1
mS mIS (i.e. S is still inverted and very little transfer from S)
h(t) = (Iz(t) - Iz0)/ Iz0 = 2stmm IS
m
The NOE enhancement is proportional to sIS !

9. Longer mixing times
a system of coupled differential equations can be solved
by diagonalization or by numerical integration
Multi-exponential solution: the exponentials are the
Eigenvalues of the relaxation matrix

10. NOESY
The selective S inversion is replaced
with a t1evolution period
Sz(0)=cosWSt1Sz0, Iz(0)=cosWIt1Iz0
(using the initial rate appx.)
Sz(tm)=sIStmIz0 + rStmSz0 (a)
+cosWIt1[sIStm]Iz0 (b)
+cosWSt1[rStm-1]Sz0 (c)

11. NOE vs. ROE
Enhancement
NOE goes through zero wtc
NOE
~10 kDa ~33kDa Small peptides
~1 kDa

12. ROESY
90
t1
tm
" wSL << wo, w * tc << 1
• The analysis of a 2D ROESY is pretty much the same than
for a 2D NOESY, with the exception that all cross-peaks are
the same sign (and opposite sign to peaks in the diagonal).
Also, integration of volumes is not as accurate…
90s
tm

13. t Approaches to Identifying NOEs
• 15N- or 13C-dispersed
(heteronuclear)
3D
1H
13C
1H
1H
15N
1H
1H
15N
1H
13C
1H
13C
1H
13C
1H
15N
1H
15N
4D
2D 1H 1H
3D 1H 1H 1H
• 1H-1H (homonuclear)

14. 2D - 3D NOE
3D- NOESY-HSQC

15. 4D NH-NH NOE
N1 – H1 H2 – N2
N1
H1
N2
H2