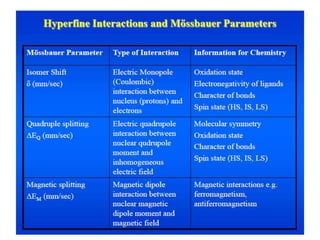
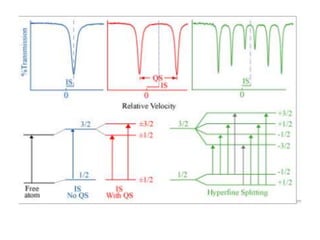
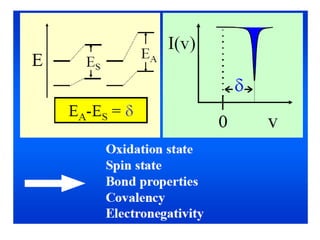
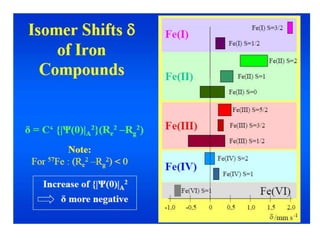
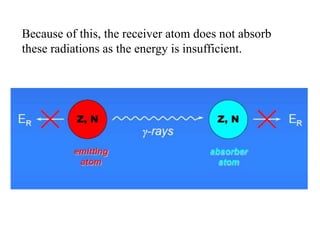
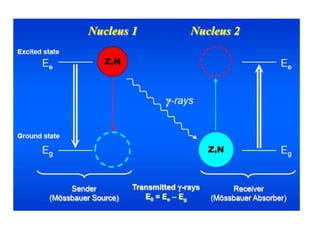
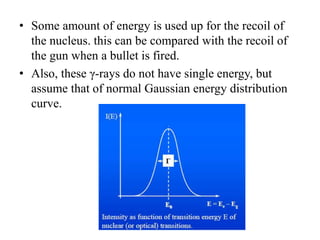
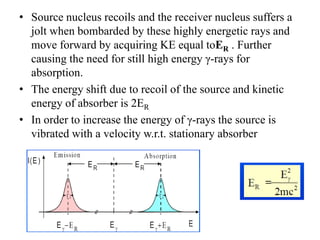
Mössbauer spectroscopy involves the interaction of gamma rays with atoms and molecules. It provides information about the chemical environment and oxidation states of atoms based on how they absorb gamma rays. For the Mössbauer effect to occur, the emitting and absorbing atoms must be embedded in a solid crystal lattice to minimize recoil effects. This allows the resonant absorption of gamma rays. Analysis of parameters like isomer shift, electric quadrupole interactions, and magnetic interactions in the Mossbauer spectrum provide details about the chemical environment and oxidation state of atoms in a sample.

1. Mössbauer
Spectroscopy
Department Of Chemistry

2. Introduction
• Deals with the interaction of γ-rays with the
atoms/molecules. Also called Nuclear Gamma
Resonance Spectroscopy
• γ-rays being highly energetic, interact with only the
nucleus of the atoms
• Wherein information about the chemical environment
and oxidation states of the atoms can be obtained
• Ex. In the compound, Fe3+[FeIII(CN)6], there are two iron
atoms in 3+ oxidation state. Both of them are in different
chemical environment. One atom within the coordination
sphere and another outside. From MB spectroscopy it is
possible to identify this.

3. MB spectrum of Fe3+[FeIII(CN)6]

4. • Advantage - gives very accurate information about
the chemical environment of similar atoms present in
a molecule and their oxidation states
• Disadvantages - Resonance absorption of γ-rays,
unlike other radiations, is not possible. Also, in order
to have a γ-ray source, an atom should be radioactive
with enough half life.
• Hence, this method cannot be employed to study all
the molecules.

5. Mössbauer effect
• Resonance absorption of γ-rays is not possible unless
certain conditions are met.
• In the other methods of spectroscopy, characteristic
absorption and emission of radiations have been
discussed
• If radiations from an excited atom are passed through
the atoms of the same element(in gaseous and ground
state), these radiations are absorbed by those atoms.
This is termed as resonance absorption.

6. Because of this, the receiver atom does not absorb
these radiations as the energy is insufficient.

8. Principles of Mossbauer effect
• γ-rays are emitted by an excited nucleus.
• These rays should possess the energy equivalent to
the energy difference between the excited and ground
states, ie, Eγ = Eg - E0
• It is observed that the energy of γ-rays has been found
to be less than the energy difference.
• This reduction is attributed to recoil of the nucleus at
the time of ejection of γ-rays.

9. • Some amount of energy is used up for the recoil of
the nucleus. this can be compared with the recoil of
the gun when a bullet is fired.
• Also, these γ-rays do not have single energy, but
assume that of normal Gaussian energy distribution
curve.

10. • Source nucleus recoils and the receiver nucleus suffers a
jolt when bombarded by these highly energetic rays and
move forward by acquiring KE equal toER . Further
causing the need for still high energy γ-rays for
absorption.
• The energy shift due to recoil of the source and kinetic
energy of absorber is 2ER
• In order to increase the energy of γ-rays the source is
vibrated with a velocity w.r.t. stationary absorber

11. • In order to make the absorption of γ-rays possible, these two
curves should overlap to the maximum extent.
• Rudolf Mossbauer, in 1958, made it possible.
• He demonstrated feasibility of the absorption of γ-rays by the
receiver atom.
• He successfully employed the phenomenon of Doppler
broadening and made the absorption possible which is termed as
Mossbauer effect.

12. • Absorption of gamma rays was achieved by
Doppler broadening ie, by changing energy of
gamma rays by a wide range.
• The absorption was made possible by reducing
both the recoil of source and acquiring of
kinetic energy by the receiver.
• The velocity

13. DOPPLER BROADENED CURVE

14. • Mossbauer showed that recoilless emission and
absorption of γ-rays becomes possible when both the
emiiting and absorbing atoms are embedded in solid
crystal lattice.
• From the equation it is evident that the recoil energy
is inversely proportional to the mass, which reduces
the usage of energy for the recoil.

15. Arrangement of source and absorber
• Source is placed on a vibrator whose velocity can
be measured
•Vibration of the source, w.r.t. stationary absorber,
covers the wide range of energy so that γ-rays of
suitable energy are absorbed

16. γ-ray Sources
• The energy of nuclear
transition must be large enough
to give, useful γ-ray photon ; but
not large enough to cause recoil
effect.
• The energy of the γ-ray photon
must be in the range of 10 –
150keV
• A substantial amount of the
nuclear decay
•must be with γ-ray emission

17. • Radioactive 57Co has 270 days halflife
• Diffused into a noble metal like rhodium, serves as
the gamma radiation source
• 57Co decays by electron capture to 57Fe with 136 keV
and nuclear spin I = 5/2
• This excited state decays after 10 ns and populates
with 85 % to 14.4 keV, I = 3/2
• 14.4 keV nuclear state has a halflife of 100 ns
• Both the halflife and the emitted gamma quanta of
14.4 keV energy are ideally suited for 57Fe Mössbauer
spectroscopy

19. Periodic table of the elements marked in red are the elements for
which the Mössbauer effect has been observed.

20. • Transition energies beyond 180 keV cause too large
recoil effects which destroy the resonance
• Gamma quanta with energies less than 5 keV will be
absorbed in the source and absorber material.
• Hence these are not suitable for Mössbauer
spectroscopy
• The ground state of the isotope should be stable. Its
natural abundance should be high or at least the
enrichment of that isotope should be easy.
• The absorption cross section should be high.

21. • Mössbauer effect has been detected for nearly 90 γ-
ray transitions in 72 isotopes of 42 different elements.
• Due to several criteria (suitable lifetime of nucelar
excited state, transition energy, easy accessibility and
handling) only twenty elements an be studied by
Mössbauer spectroscopy
• E.g. Iron, Tin, Antimony, Tellurium, Iodine, Gold,
Nickel, Ruthenium, Iridium, Tungsten, Krypton,
Xenon, many of the rare earth elements, Neptunium.

22. Recording the MB spectrum
•MB spectrum is recorded
by plotting relative
transmission vs Doppler
velocity ie., velocity with
which the emitter is
vibrated
•The peak at Doppler
velocity zero means both
the emitter and absorber
are in the same chemical
environment

23. INSTRUMENTATION

24. • Source is generally kept at room temperature.
• Absorber (sample under study) may be cooled down
to liquid nitrogen or liquid helium temperatures in a
cryostat, or for controlled heating in an oven
• γ-rays are detected by a scintillation counter, gas
proportional counter or a semi-conductor detector
• A constant frequency clock synchronises a voltage
waveform which serves as a reference signal to the
servo-amplifier controlling the electro-mechanical
vibrator.

25. Isomer shift
• One of the important parameters which give information
about the chemical environment and the oxidation state of
the absorber
• Isomer shift, δ, is observed when source nucleus and
absorber nucleus are in different chemical environment.
• Transition energy is affected by the interaction between
the nucleus and the electrons present around it.
• This arises because of the reason that the nucleus will
have different sizes in ground and excited states.
• The change in nuclear radius when going from g.s to e.s
is ΔR

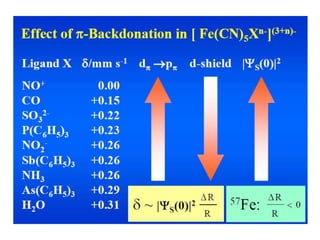
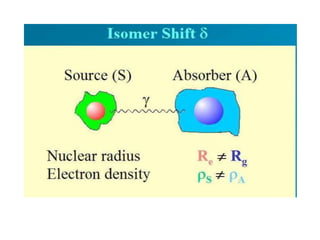
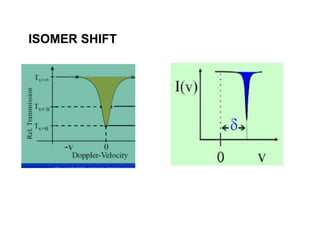
26. • The isomer shift can be calculated by the following
equation.
• δ= (εo /5) (Ze2R2)(Δ R/R)[|ψs(abs)|2-|ψs(source)|2]
• where
εo– Permittivity of free space
Z - atomic number of the nucleus
e - electronic charge
ψs(abs) - s orbital wave function of absorber
ψs(source) - s orbital wave function of source

28. • s electron density affects the isomer shift to a great
extent
• Changes in p & d orbital occupancies affect the s
electron through screening hence have a smaller
effect on isomer shift
• When ΔR/R is positive the isomer shift is also
positive and negative when ΔR/R is negative
• When both absorber and emitter nuclei are in same
chemical environment then isomer shift occurs at zero
Doppler velcity. If the chemical environment is
different isomer shift is either more or less than zero

29. ISOMER SHIFT

30. Isomer shift values for Fe compounds
• Fe isomer shift cannot be used for determining the
O.S of Fe in a molecule.
• Fe O.S from 0 to 4, often differ in unit charge only.
• The electrons involved are from d orbital. So effect
on the s electrons is smaller.
• Different spin states also affect the shift value.
• Selection Rule for MB spectra mI = 0, 1

31. • Fe can be present in +2 or +3 state in Fe-porphyrin.
• Complexes can be easily reduced. The electron may
be transferred either to Fe or to the ligand.
• In that ambiguous case MB spectra is useful in
determining the O.S
• Isomer shifts are measured relative to a standard for
57Fe – [Fe(CN)5NO] and for 119Sn-SnO2

32. • Isomer shift is related to the oxidation state of the
metal.
• In 119Sn MB spectra Sn(II) shows a positive shift
(ΔR/R ) w.r.t. Sn where as for Sn(IV) it is negative

33. • In 119Sn compounds, the shift values depend on the
ligands present and the coordination number
• Isomer shift values are useful in characterizing tin
derivatives
• Many Sn compounds appear to contain Sn(II) from
the formulae but MB spectral data shows Sn(IV) is
present in them.

34. Electric Quadruple Interactions
• Nuclei with I >1/2 have a non-spherical charge
distribution.
• This produces a nuclear quadruple moment.
• In the presence of an asymmetrical electric field the
nuclear energy levels split
OBLATE PROLATE

35. • In the case of an isotope with I=3/2 excited state,
such as 57Fe or 119Sn, the excited state is split into two
sub states mI=±1/2,±3/2.
• This gives a two line spectrum or 'doublet‘. The
magnitude of splitting, Delta Δ, is related to the
nuclear quadrupole moment, Q,
• Δ=eQqzz/2
• It is known that nuclei with
I>1/2 exhibit quad.energy
levels which split due to
asymmetry

38. • Quadruple splitting shows the presence of efg at the
nucleus.
• The efg may be created by the ligand field or by the
electron distribution around the nucleus.
• Single crystal or application of magnetic field gives
more information.
• If a nucleus with symmetric electron distribution is in
an Oh field, efg is not expected.

39. Magnetic interactions
• In the presence of a magnetic field the nuclear spin
moment experiences a dipolar interaction thereby
causing splitting of spectral lines ie., Zeeman splitting
• There are many sources of magnetic fields that can be
experienced by the nucleus
• The total effective magnetic field at the nucleus, Beff is
given by
• Beff = (Bcontact + Borbital ) + Bapplied
• Bcontact - spin of electrons polarising the spin density at
the nucleus
• Borbital - orbital moment on those electrons

40. • This magnetic field splits nuclear levels with a spin of
I into (2I+1) substates.
• Transitions between the excited state and ground state
can only occur where mI changes by 0 or 1.
• This gives six possible transitions for a 3/2 to 1/2
transition, giving a sextet with the line spacing being
proportional to Beff

41. Effect of magnetic field on MB
Spectrum of 57Fe

42. APPLICATIONS
• Spectra of spin free Fe(II) – FeSO4.7H2O

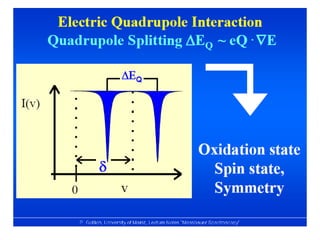
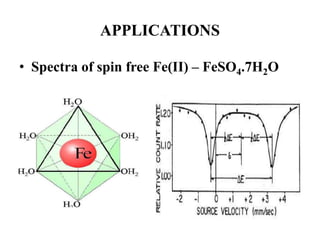
43. • Based on crystallographic data it was thought that
FeSO4.7H2O possesses perfect Oh symmetry with six H2O
on each vertex.
• But the MB spectrum shows a large quadruple splitting,
which is not possible in a regular Oh symmetry, for a
perfect Oh field efg is zero
• Similar spectrum is obtained for [Fe(H2O)6]2+
• Fe(II) is a d6 system and H2O being a weak ligand forms
high spin complex retaining orbital degeneracy
• This leads to Jahn-Teller distortion and removes orbital
degeneracy causing efg at the nucleus

44. • Fe(II) is a d6 system and orbital degeneracy is
retained as H2O is a weak ligand
• This causes J-T distortion to remove the
degeneracy in a tetragonal field.
• This creates an efg at the nucleus and hence
quadruple splitting.
• The structure assigned is distorted Ohwith all
angles 90o with x ≠ y ≠ z

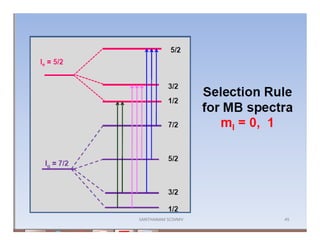
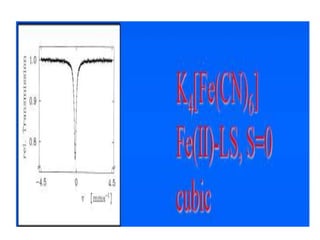
45. • This efg at the nucleus leads to quadruple
splitting.
• Hence, two transitions are seen in the spectrum
• The structure assigned is distorted Ohwith all
angles 90o with x ≠ y ≠ z
• MB spectum of K4[Fe(CN)6] shows a single line
indicating perfect octahedral structure with
efg=0

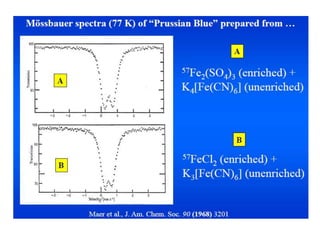
47. Prussian Blue and Turnbull’s blue
• Prussian blue is a dark blue pigment with the
idealized formula Fe7(CN)18. it is prepared by adding
a ferric salt to ferrocyanide
• Turnbull's blue is prepared by adding ferrous salts to
ferricyanide.
• Prussian Blue with [FeII(CN)6]4- anions and
Turnbull’s Blue with [FeIII(CN)6]3- anions, according
to the different way of preparing them.
• Mössbauer spectra of these are almost identical

49. • This was confirmed by using K4[FeII(CN)6] and
K3[FeIII(CN)6] as reference compounds.
• Immediately after adding a solution of Fe2+ to a
solution of [FeIII(CN)6]3- a rapid electron transfer
takes place from Fe2+ to the anion [FeIII(CN)6]3- with
subsequent precipitation of the same material
• A singlet for Fe(II) and a quadruple doublet for
Fe(III) were which confirmed Prussian blue and
Turnbull’s blue are identical

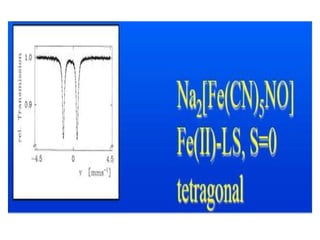
50. Sodium nitroprusside – Na2[Fe(CN)5(NO)]
• Initially it was assumed that it contained Fe(II) and
NO+ since it is diamagnetic. [Fe(II)-d6; Fe(III) –d5]
• But the MB spectrum of the sample showed a doublet
with δ = -0.165 mm/S
• This value is too negative for a Fe(II) complex.
• This suggests that the Fe may be in Fe(IV) state.
• The magnetism and MB spectrum are in consistent with
the structure which has an extensive π-bonding with
NO+ ligand .
• The t2g orbitals of Fe and the p-orbital of N present in
NO+ containing the odd e-, to form a π-bond

52. • The Fe(II) is transferring the electrons form filled t2g
level to the vacant π- antibonding orbital of NO.
• This loss of electrons makes the isomer shift value to
approach Fe(IV) values.
• Now because of this the shielding of s electrons by the
d electrons decrease and hence the increase in shift
• This is supported by the decrease in N-O stretching
frequency in IR, since the anti bonding level is filled.

53. Ferredoxin
• Study of ferredoxin, a Fe-S protein, which assists in
in-vivo electron transfer reactions
• The two-iron centres are not equivalent in the reduced
form.
• The oxidized form with two Fe(III)-high spin centres
can be distinguished from the reduced form with one
Fe(III)-high spin centre and one Fe(II)-high spin
centre only by using MB spectrum

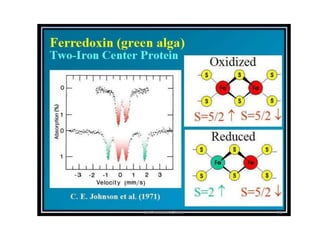
55. Study of thermal spin-cross over
• Many coordination compounds possessing intermediate
ligand field strengths show thermal spin crossover. [ i.e.
HS <--> LS]
• Fe(phen)2(NCS)2 undergoes thermal spin transition .
• The main result is that in the temperature region, where
the MAS spectra reflect the transition to the LS state,
the MES spectra still show the typical HS signals
arising from excited ligand field

64. Thank you
👍