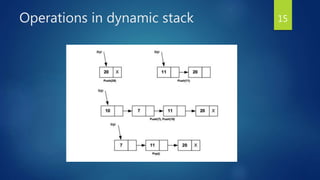
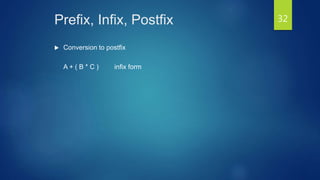
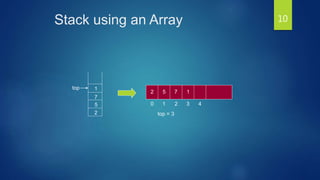
The document discusses stacks and their implementation and use. It begins by defining a stack as a collection of items that can be inserted or deleted from one end, following the LIFO principle. Common stack operations like push, pop and top are introduced. Stacks can be implemented using arrays or linked lists. The use of stacks to evaluate expressions in prefix, infix and postfix notations is covered, including the precedence of operators and the process to convert infix to postfix notation using a stack. Parentheses are also discussed in the conversion process.

1. Data Structures
Lecture 3
RUBYA AFRIN
NORTHERN UNIVERSITY OF BUSINESS AND TECHNOLOGY

2. Stack
 A stack is a collection of items into which items can be
inserted or deleted at one end.
 A stack implements the LIFO (Last In First Out)protocol
2

3. Stacks
 Stacks in real life: stack of books, stack of plates
 Add new items at the top
 Remove an item at the top
 Stack data structure similar to real life: collection of elements
arranged in a linear order.
 Can only access element at the top
3

4. Stack Operations
 Push(X) – insert X as the top element of the stack
 Pop() – remove the top element of the stack and return it.
 Top() – return the top element without removing it from the stack.
4

5. Stack Operations
push(2)
top 2
push(5)
top
2
5
push(7)
top
2
5
7
push(1)
top
2
5
7
1
1 pop()
top
2
5
7
push(21)
top
2
5
7
21
21 pop()
top
2
5
7
7 pop()
2
5top
5 pop()
2top
5

6. Stack Operation
 The last element to go into the stack is the first to come out: LIFO –
Last In First Out.
 What happens if we call pop() and there is no element?
 Have IsEmpty() boolean function that returns true if stack is empty,
false otherwise.
 Throw StackEmpty exception: advanced C++ concept.
6

7. Stack Operation
 Overflow: occurs if we try to insert an item into an array
which is full
 Underflow: occurs when we try to retrieve an item form
an empty list
7

8. Push Operation
 If the stack is full, print an error message (overflow)
 Make place for new item by incrementing top
 Put the item in place
8

9. Pop Operation
 If the stack is empty, print an error message an halt
execution (underflow)
 Remove the top element from the stack
 Return the element to the calling program
9

10. Stack using an Array
top
2
5
7
1
2 5 7 1
0 1 32 4
top = 3
10

11. Stack using an Array
 In case of an array, it is possible that the array may “fill-up” if we
push enough elements.
 Have a boolean function IsFull() which returns true is stack
(array) is full, false otherwise.
 We would call this function before calling push(x).
11

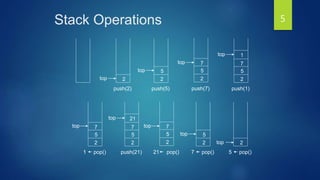
12. Stack Operations with Array
int pop()
{
return A[current--];
}
void push(int x)
{
A[++current] = x;
}
12

13. Stack Operations with Array
int top()
{
return A[current];
}
int IsEmpty()
{
return ( current == -1 );
}
int IsFull()
{
return ( current == size-1);
}
 A quick examination shows that all five operations take constant
time.
13

14. Stack Using Linked List
 We can avoid the size limitation of a stack implemented with an
array by using a linked list to hold the stack elements.
 As with array, however, we need to decide where to insert elements
in the list and where to delete them so that push and pop will run the
fastest.
14

15. Operations in dynamic stack 15

16. Use of Stack
 Example of use: prefix, infix, postfix expressions.
 Consider the expression A+B: we think of applying the operator “+”
to the operands A and B.
 “+” is termed a binary operator: it takes two operands.
 Writing the sum as A+B is called the infix form of the expression.
16

17. Prefix, Infix, Postfix
 Two other ways of writing the expression are
+ A B prefix
A B + postfix
 The prefixes “pre” and “post” refer to the position of the operator with
respect to the two operands.
17

18. Prefix, Infix, Postfix
 Consider the infix expression
A + B * C
 We “know” that multiplication is done before addition.
 The expression is interpreted as
A + ( B * C )
 Multiplication has precedence over addition.
18

19. Prefix, Infix, Postfix
 Conversion to postfix
(A + B ) * C infix form
19

20. Prefix, Infix, Postfix
 Conversion to postfix
(A + B ) * C infix form
( A B + ) * C convert addition
20

21. Prefix, Infix, Postfix
 Conversion to postfix
(A + B ) * C infix form
( A B + ) * C convert addition
( A B + ) C * convert multiplication
21

22. Prefix, Infix, Postfix
 Conversion to postfix
(A + B ) * C infix form
( A B + ) * C convert addition
( A B + ) C * convert multiplication
A B + C * postfix form
22

23. Precedence of Operators
 The five binary operators are: addition, subtraction, multiplication,
division and exponentiation.
 The order of precedence is (highest to lowest)
 Exponentiation 
 Multiplication/division*, /
 Addition/subtraction +, -
23

24. Infix to Postfix
Infix Postfix
A + B A B +
12 + 60 – 23 12 60 + 23 –
(A + B)*(C – D ) A B + C D – *
24

25. Converting Infix to Postfix
 Example: A + B * C
symb postfix stack
A A
25

26. Converting Infix to Postfix
 Example: A + B * C
symb postfix stack
A A
+ A +
26

27. Converting Infix to Postfix
 Example: A + B * C
symb postfix stack
A A
+ A +
B AB +
27

28. Converting Infix to Postfix
 Example: A + B * C
symb postfix stack
A A
+ A +
B AB +
* AB + *
28

29. Converting Infix to Postfix
 Example: A + B * C
symb postfix stack
A A
+ A +
B AB +
* AB + *
C ABC + *
29

30. Converting Infix to Postfix
 Example: A + B * C
symb postfix stack
A A
+ A +
B AB +
* AB + *
C ABC + *
ABC * +
30

31. Converting Infix to Postfix
 Example: A + B * C
symb postfix stack
A A
+ A +
B AB +
* AB + *
C ABC + *
ABC * +
ABC * +
31

32. Prefix, Infix, Postfix
 Conversion to postfix
A + ( B * C ) infix form
32

33. Prefix, Infix, Postfix
 Conversion to postfix
A + ( B * C ) infix form
A + ( B C * ) convert multiplication
33

34. Prefix, Infix, Postfix
 Conversion to postfix
A + ( B * C ) infix form
A + ( B C * ) convert multiplication
A ( B C * ) + convert addition
34

35. Converting Infix to Postfix
 Handling parenthesis
 When an open parenthesis ‘(‘ is read, it must be pushed on the
stack.
 This can be done by setting prcd(op,‘(‘ ) to be FALSE.
 Also, prcd( ‘(‘,op ) == FALSE which ensures that an operator after ‘(‘
is pushed on the stack.
35

36. Converting Infix to Postfix
 When a ‘)’ is read, all operators up to the first ‘(‘ must be popped and
placed in the postfix string.
 To do this, prcd( op,’)’ ) == TRUE.
 Both the ‘(‘ and the ‘)’ must be discarded: prcd( ‘(‘,’)’ ) == FALSE.
 Need to change line 11 of the algorithm.
36

37. Prefix, Infix, Postfix
 Conversion to postfix
A + ( B * C ) infix form
A + ( B C * ) convert multiplication
A ( B C * ) + convert addition
A B C * + postfix form
Symbol
Scanned
Stack Postfix
Notation
A empty A
+ + A
( +,( A
B +,( AB
* +,(,* AB
C +,(,* ABC
) ABC*+
37